Exponenta Banner

Inverse Kinematics

Вычислите строения соединений, чтобы достичь положения end-effector

развернуть все на странице
  • Библиотека:

  • Алгоритмы Robotics System Toolbox/Manipulator

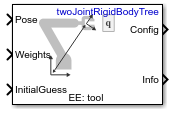
  • Inverse Kinematics block

Описание

Блок Inverse Kinematics использует обратный кинематический (IK) решатель, чтобы вычислить строения соединений для желаемого положения end-effector на основе заданной модели древовидного твердого тела. Создайте модель древовидного твердого тела для вашего робота с помощью rigidBodyTree класс. Модель древовидного твердого тела задает все ограничения соединений, которые применяет решатель.

Задайте RigidBodyTree параметр и требуемый концевой эффектор внутри маски блока. Можно также настроить параметры алгоритма на вкладке Solver Parameters.

Введите требуемый концевой эффекторный Pose, Weights на допуск положения и InitialGuess для строения соединения. Решатель выводит строение робота, Config, которая удовлетворяет положению end-effector в пределах допусков, заданных на вкладке Solver Parameters.

Порты

Вход

расширить все

Положение end-effector, заданное как однородное преобразование 4 на 4. Это преобразование определяет желаемое положение и ориентацию твердого тела, заданные в параметре End effector.

Типы данных: single | double

Веса для допусков положения, заданные как вектор с шестью элементами. Первые три элемента вектора соответствуют весам на ошибке в ориентации для желаемого положения. Последние три элемента вектора соответствуют весам на ошибке в xyz положении для желаемого положения.

Типы данных: single | double

Исходное предположение строения робота, заданное как вектор положений соединений. Количество положений равно количеству нефиксованных соединений в параметре Rigid body tree. Используйте эту начальную догадку, чтобы помочь привести решатель к желаемому строению робота. Однако решение не гарантировано близко к этому исходному предположению.

Типы данных: single | double

Выход

расширить все

Строение робота, которая решает желаемое положение end-effector, заданное как вектор. Строение робота является вектором положений соединений для модели древовидного твердого тела. Количество положений равно количеству нефиксованных соединений в параметре Rigid body tree.

Типы данных: single | double

Информация о решении, возвращенная как шина. Информационная шина решения содержит следующие элементы:

  • Iterations - Количество итераций, выполняемых алгоритмом.

  • PoseErrorNorm Величина ошибки между положением концевого эффектора в решении и желаемым концевым эффекторным положением.

  • ExitFlag - Код, который приводит более подробную информацию о выполнении алгоритма и о том, что заставило его вернуться. Флаги выхода каждого типа алгоритма см. в разделе Флаги выхода.

  • Status - Вектор символов, описывающий, находится ли решение в пределах допуска (1) или является наилучшим возможным решением, которое может найти алгоритм (2).

Параметры

расширить все

Параметры блоков

Модель древовидного твердого тела, заданная как rigidBodyTree объект. Создайте модель робота в MATLAB® рабочей области перед указанием в маске блока.

Имя конечного эффектора для требуемого положения. Чтобы увидеть список тел на rigidBodyTree задайте параметр Rigid body tree, затем нажмите Select body.

Выберите, чтобы включить порт Info и получить диагностическую информацию для решения решателя.

Параметры решателя

Алгоритм решения обратной кинематики, заданный как 'BFGSGradientProjection' или 'LevenbergMarquardt'. Для получения дополнительной информации о каждом алгоритме, см. «Алгоритмы обратной кинематики».

Выберите, чтобы применить пределы соединений, заданные в модели Rigid body tree.

Максимальное количество итераций для оптимизации решения, заданное в виде положительного целого числа. Увеличение количества итераций может улучшить решение за счет времени выполнения.

Максимальное количество секунд, которое алгоритм запускает перед тайм-аутом, заданное как положительная скалярная величина. Увеличение максимального времени может улучшить решение за счет времени выполнения.

Порог на градиент функции затрат, заданный как положительная скалярная величина. Алгоритм останавливается, если величина градиента падает ниже этого порога. Низкая величина градиента обычно указывает, что решатель сходился к решению.

Порог на величину ошибки между положением end-effector, сгенерированным из решения, и желаемым положением, заданным как положительная скалярная величина. The Weights указанные для каждого компонента положения включены в этот расчет.

Минимальный размер шага, разрешенный решателем, задается как положительная скалярная величина. Меньшие размеры шага обычно означают, что решение близко к сходимости.

Порог на изменение в end-effector положения ошибка между итерациями, заданная как положительная скалярная величина. Алгоритм возвращается, если изменения во всех элементах ошибки положения меньше этого порога.

Зависимости

Этот параметр активируется, когда Solver Levenberg-Marquadt.

Установите флажок, чтобы включить демпфирование при ошибке, затем задайте Damping bias параметр.

Зависимости

Этот параметр активируется, когда Solver Levenberg-Marquadt.

Демпфирование функции стоимости, заданное как положительная скалярная величина. Алгоритм Левенберга-Марквадта имеет признак демпфирования, управляемый этим скаляром, который работает с функцией затрат, чтобы контролировать скорость сходимости.

Зависимости

Этот параметр активируется, когда Solver Levenberg-Marquadt а Use error damping есть on.

  • Interpreted execution - Моделируйте модель с помощью интерпретатора MATLAB. Эта опция сокращает время запуска, но имеет более низкую скорость симуляции, чем Code generation. В этом режиме можно отлаживать исходный код блока.

  • Code generation - Моделируйте модель с использованием сгенерированного кода C. Первый раз, когда вы запускаете симуляцию, Simulink® генерирует код С для блока. Код С повторно используется для последующих симуляций, пока модель не меняется. Эта опция требует дополнительного времени запуска, но скорость последующих симуляций сопоставима с Interpreted execution.

Настраиваемый: Нет

Примеры моделей

Trace An End-Effector Trajectory with Inverse Kinematics in Simulink

Проследите конечную эффекторную траекторию с обратной кинематикой в Simulink

Используйте модель робота тела для вычисления обратной кинематики с помощью Simulink ®. Задайте траекторию для эффектора конца робота и цикла через точки, чтобы решить строения робота, которые отслеживают эту траекторию.

Ссылки

[1] Бадреддин, Хассан, Стефан Вандевалль и Йохан Мейерс. Последовательное квадратичное программирование (SQP) для оптимального управления при прямой числовой симуляции турбулентного потока. Журнал вычислительной физики. 256 (2014): 1–16. doi: 10.1016/j.jcp.2013.08.044.

[2] Bertsekas, Dimitri P. Нелинейное программирование. Belmont, MA: Athena Scientific, 1999.

[3] Голдфарб, Дональд. Расширение метода переменной метрики Дэвидона до максимизации при линейном неравенстве и ограничениях равенства. SIAM Journal по прикладной математике. Том 17, № 4 (1969): 739-64. doi: 10.1137/0117067.

[4] Нокедал, Хорхе и Стивен Райт. Численная оптимизация. Нью-Йорк, Нью-Йорк: Спрингер, 2006.

[5] Сугихара, Томомичи. «Разрешимость-неконтролируемая обратная кинематика методом Левенберга-Марквардта». Транзакции IEEE по робототехнике. Том 27, № 5 (2011): 984-91. doi: 10.1109/tro.2011.2148230.

[6] Чжао, Цзяньминь и Норман И. Бадлер. «Позиционирование обратной кинематики с использованием нелинейного программирования для высоко сочлененных фигур». Транзакции ACM на графике. Том 13, № 4 (1994): 313-36. doi: 10,1145/ 195826,195827.

Расширенные возможности

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ Simulink ®

.

См. также

Объекты

Блоки

Темы

Введенный в R2018b

Документация по Robotics System Toolbox

Поддержка