Метод H ∞ со смешанной чувствительностью для проекта устойчивого контура управления
[ вычисляет контроллер, который минимизирует H ∞ норму взвешенной передаточной функции с обратной связьюK,CL,gamma,info] = mixsyn(G,W1,W2,W3)
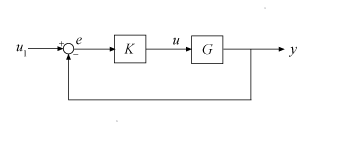
где S = (I + GK)–1 и T = (I - S) является дополнительной чувствительностью следующей системы управления.
Вы выбираете функции взвешивания W1,W2,W3 для формирования частотных характеристик для отслеживания и подавления помех, усилия контроллера и снижения шума и робастности, соответственно. Для получения дополнительной информации о том, как выбрать функции взвешивания, смотрите Mixed-Sensitivity Loop Shaping.
mixsyn вычисляет контроллер K что приводит к минимальному ||<reservedrangesplaceholder2> (s) ||∞, который возвращается следующим gamma. Для возвращенного K контроллера,
[ вычисляет контроллер для целевого уровня эффективности K,CL,gamma] = mixsyn(G,W1,W2,W3,gamTry)gamTry. Определение gamTry может быть полезным, когда оптимальная эффективность контроллера лучше, чем вам нужно для вашего приложения. В этом случае менее оптимальный контроллер может иметь меньшие усиления и быть лучше обусловлен численно. Когда W1,W2,W3 захватывать желаемые пределы коэффициентов усиления S, KS и T, использовать gamtry = 1, чтобы просто применить эти пределы.
Если gamTry не достижимо, mixsyn возвращает [] для K и CL, и Inf для gamma.
[ выполняет поиск по области значений K,CL,gamma] = mixsyn(G,W1,W2,W3,gamRange)gamRange для достижения наилучшей эффективности. Задайте область значений с вектором формы [gmin,gmax]. Ограничение области значений поиска может ускорить расчет, уменьшив количество итераций, выполненных mixsyn для тестирования различных уровней эффективности.
[ задает дополнительные опции расчета. Создание K,CL,gamma] = mixsyn(___,opts)opts, использование hinfsynOptions. Задайте opts после всех других входных параметров.
Использование mixsyn для чувствительности и дополнительной чувствительности цикла формирования. Создайте модель объекта управления и весовые функции, которые:
Сформируйте функцию чувствительности для отслеживания уставки и подавления помех (W1 = 1/S большой внутри управляющей полосы).
Сформируйте дополнительную чувствительность к робастности и шумовому ослаблению (W3 = 1/T большой вне полосы пропускания управления).
Ограничьте усилие управления (W2 = 1/KS большой внутри управляющей полосы).
(Для получения дополнительной информации о выборе функций взвешивания смотрите Mixed-Sensitivity Loop Shaping.)
s = zpk('s');
G = (s-1)/(s+1)^2;
W1 = makeweight(10,[1 0.1],0.01);
W2 = makeweight(0.1,[32 0.32],1);
W3 = makeweight(0.01,[1 0.1],10);
bodemag(W1,W2,W3)
Проектируйте контроллер.
[K,CL,gamma] = mixsyn(G,W1,W2,W3);
mixsyn формирует сингулярные значения функции чувствительности S, дополнительную функцию чувствительности Tи усилие по управлению R = K*S. Исследуйте результаты синтеза и формы этих передаточных функций.
S = feedback(1,G*K); KS = K*S; T = 1-S; sigma(S,'b',KS,'r',T,'g',gamma/W1,'b-.',ss(gamma/W2),'r-.',gamma/W3,'g-.',{1e-3,1e3}) legend('S','KS','T','GAM/W1','GAM/W2','GAM/W3','Location','SouthWest') grid
G - ОбъектОбъект, заданный как динамическая системная модель, такая как пространство состояний (ss) модель. G может быть любой моделью LTI. mixsyn принимает следующую структуру управления.
Если G является обобщенной моделью пространства состояний с неопределенными или настраиваемыми блоками системы управления, затем mixsyn использует номинальное или текущее значение этих элементов.
W1,W2,W3 - Функции взвешивания[]Функции взвешивания, заданные как динамическая система модели. Выберите функции взвешивания W1,W2,W3 для формирования частотных характеристик для отслеживания и подавления помех, усилия контроллера и снижения шума и робастности. Как правило:
Для хорошей эффективности отслеживания уставки и подавления помех выберите W1 большая внутри управляющей полосы для получения малых S.
Для ослабления робастности и шума выберите W3 большой вне управляющей полосы для получения малых T.
Чтобы ограничить усилие управления в конкретном диапазоне частот, увеличьте амплитуду W 2 в этом диапазоне частот, чтобы получить малую KS.
Если один из весов не нужен, установите его равным []. Например, если вы не хотите ограничивать усилия по управлению, используйте W2 = [].
Использовать makeweight создание весовых функций с желаемыми профилями усиления. Для получения дополнительной информации о выборе функций взвешивания смотрите Mixed-Sensitivity Loop Shaping.
Если G имеет NU входы и NY выходы, затем W1,W2,W3 должны быть либо SISO, либо квадратные системы размера NY, NU и NY, соответственно.
Потому что S + T = I, mixsyn невозможно сделать S и T маленькими (менее 0 дБ) в одной частотной области значений. Поэтому, когда вы задаете веса для формирования цикла, должен быть полоса частот, в котором оба W1 и W3 менее 0 дБ.
gamTry - Целевой уровень эффективностиЦелевой уровень эффективности, заданный как положительная скалярная величина. mixsyn пытается вычислить контроллер таким образом, чтобы H ∞ взвешенной системы с обратной связью M (s) не превышал gamTry. Если этот уровень эффективности достижим, то возвращенный контроллер имеет gamma ≤ gamTry. Если gamTry не достижимо, mixsyn возвращает пустой контроллер.
gamRange - область значений эффективности для поиска[0,Inf] (по умолчанию) | вектор формы [gmin,gmax]Область значений эффективности для поиска, заданный как вектор формы [gmin,gmax]. mixsyn команда проверяет только уровни эффективности в этой области значений. Он возвращает контроллер с эффективностью:
Если вы знаете область значений допустимых уровней эффективности, установка этой области значений может ускорить расчеты, уменьшив количество итераций, выполненных mixsyn для тестирования различных уровней эффективности.
opts - ОпцииhinfsynOptions объектДополнительные опции для расчета, заданные как объект опций, который вы создаете используя hinfsynOptions.
Использование opts чтобы задать опции для базовых hinfsyn расчеты (см. Алгоритмы). Доступные опции включают:
Отобразите прогресс алгоритма в командной строке.
Отключите автоматическое масштабирование и регуляризацию.
Задайте метод оптимизации.
Для получения информации обо всех опциях см. hinfsynOptions.
mixsyn использует ваши функции взвешивания для генерации дополненного объекта P = augw(G,W1,W2,W3). Затем он вызывает hinfsyn чтобы найти контроллер, который минимизирует H ∞ норму передаточной функции с обратной связью M (s) = LFT (P, K). Для получения дополнительной информации см. Раздел «Формирование цикла смешанной чувствительности ».