Постройте неявное символьное уравнение или функцию
fimplicit( строит графики неявного символьного уравнения или функции f)f в течение интервала по умолчанию [-5 5] для x и y.
fimplicit( графики f,[xmin xmax
ymin ymax])f через интервал xmin <x <xmax и ymin <y <ymax. fimplicit функция использует symvar чтобы упорядочить переменные и назначить интервалы.
fimplicit(___, использует LineSpec)LineSpec чтобы задать стиль линии, символ маркера и цвет линии.
fimplicit(___, задает свойства линий с помощью одной или нескольких Name,Value)Name,Value аргументы в виде пар. Используйте эту опцию с любыми комбинациями входных аргументов в предыдущих синтаксисах. Name,Value настройки пар применяются ко всем нанесенным на график линиям. Чтобы задать опции для отдельных линий, используйте объекты, возвращенные fimplicit.
fimplicit( графики в осях заданные ax,___)ax вместо текущей системы координат gca.
fimplicit присваивает символьные переменные в f на x ось, затем y ось, и symvar определяет порядок переменных, которые будут назначены. Поэтому имена переменных и осей могут не совпадать. Вызвать fimplicit чтобы назначить x или y ее соответствующей оси, создайте символическую функцию для построения графика, затем передайте символьную функцию fimplicit.
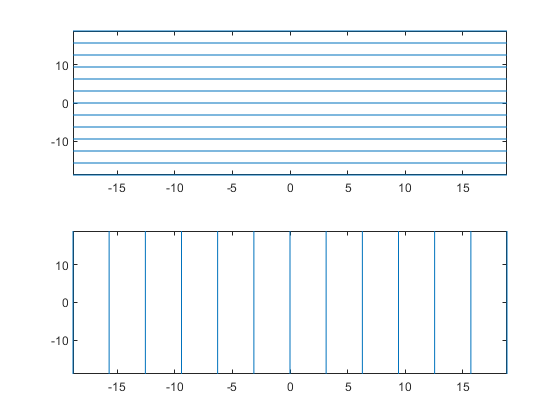
Для примера следующий код строит графики корней неявной функции f (x, y) = sin (y) двумя способами. Первый способ заставляет волны колебаться относительно оси y. Второй способ присваивает y оси x, потому что это первая (и единственная) переменная в символьной функции.
syms x y; f(x,y) = sin(y); intvl = [-6 6]*pi; figure; subplot(2,1,1) fimplicit(f,intvl); subplot(2,1,2) fimplicit(f(x,y),intvl); % Or fimplicit(sin(y) == 0,intvl);