Реализуйте αβ к преобразованию dq
Motor Control Blockset / Средства управления / Математика Преобразовывает
Блок Park Transform вычисляет преобразование Парка двухфазных ортогональных компонентов в стационарной системе координат αβ.
Блок принимает следующие входные параметры:
Компоненты осей α-β в стационарной системе координат.
Синус и значения косинуса соответствующих углов преобразования.
Это выводит ортогональный прямой и квадратурные компоненты оси во вращающейся системе координат dq. Можно сконфигурировать блок, чтобы выровнять или d - или q - ось с α - ось во время t = 0.
Рисунки показывают компоненты осей α-β в системе координат αβ и вращающейся системе координат dq для когда:
d - ось выравнивается с α - ось.
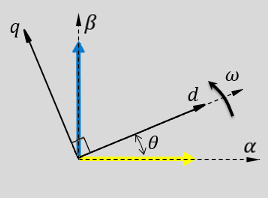
q - ось выравнивается с α - ось.
В обоих случаях, угол θ = ωt, где:
θ является углом между α - и d - осями для d - выравниванием оси или углом между α - и q - осями для q - выравнивание оси. Это указывает на угловое положение вращающейся системы координат dq относительно α - ось.
ω является скоростью вращения системы координат d-q.
t является временем, в секундах, от начального выравнивания.
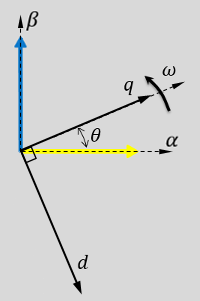
Рисунки показывают ответ времени отдельных компонентов αβ и систем координат dq когда:
d - ось выравнивается с α - ось.
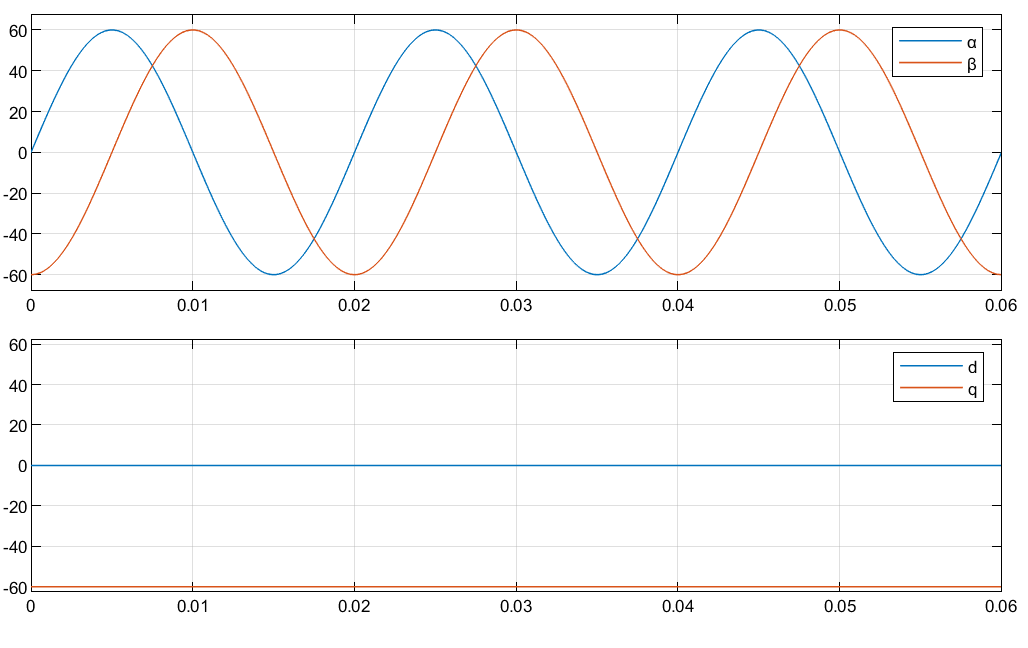
q - ось выравнивается с α - ось.
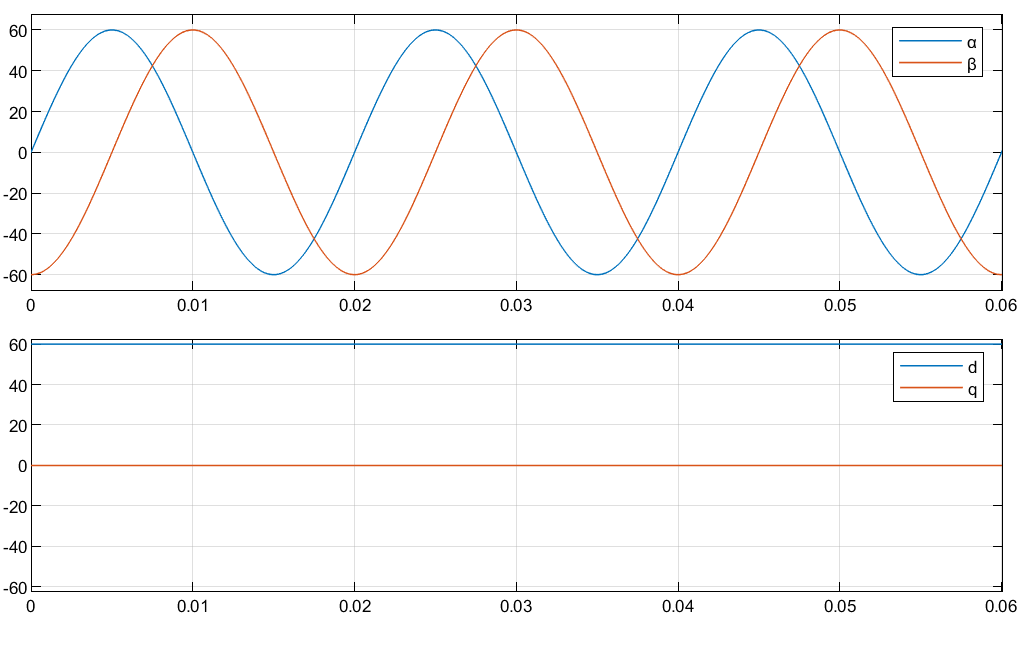
Следующие уравнения описывают, как блок реализует преобразование Парка.
Когда d - ось выравнивается с α - ось.
Когда q - ось выравнивается с α - ось.
где:
и двухфазные ортогональные компоненты в стационарной системе координат αβ.
и прямая ось и квадратурная ось ортогональные компоненты во вращающейся системе координат dq.
Inverse Park Transform | Clarke Transform | Sine-Cosine Lookup | Discrete PI Controller with anti-windup and reset | ACIM Feed Forward Control | ACIM Torque Estimator | PMSM Feed Forward Control | PMSM Torque Estimator