Построение 3-D параметрического графика

Постройте 3-D параметрический график

по параметру по умолчанию располагаются [-5 5].

syms t
xt = sin(t);
yt = cos(t);
zt = t;
fplot3(xt,yt,zt)

Определение области значений параметра

Постройте параметрический график

по параметру располагаются [-10 10] путем определения четвертого аргумента fplot3.

syms t
xt = exp(-t/10).*sin(5*t);
yt = exp(-t/10).*cos(5*t);
zt = t;
fplot3(xt,yt,zt,[-10 10])

Измените свойства строки и маркеры отображения

Постройте ту же 3-D параметрическую кривую три раза на различных интервалах параметра. Для первой кривой используйте linewidth 2. Для второго задайте пунктирный стиль красной линии с круговыми маркерами. Для третьего задайте голубой стиль штрихпунктирной линии с маркерами звездочки.

syms t
fplot3(sin(t), cos(t), t, [0 2*pi], 'LineWidth', 2)
hold on
fplot3(sin(t), cos(t), t, [2*pi 4*pi], '--or')
fplot3(sin(t), cos(t), t, [4*pi 6*pi], '-.*c')

Постройте 3-D параметрический график Используя символьные функции

Постройте 3-D параметрический график

syms x(t) y(t) z(t)
x(t) = sin(t);
y(t) = cos(t);
z(t) = cos(2*t);
fplot3(x,y,z)

Построение нескольких графиков на той же фигуре

Постройте несколько графиков или путем передачи входных параметров как вектора или при помощи hold on, чтобы последовательно построить на той же фигуре. Если вы задаете аргументы LineSpec и Name-Value, они применяются ко всем строкам. Чтобы установить опции для отдельных строк, используйте указатели на функцию, возвращенные fplot3.

Разделите фигуру на два подграфика с помощью subplot. На первом подграфике постройте два параметризованных графика с помощью векторного входа. На втором подграфике постройте те же графики с помощью hold on.

syms t
subplot(2,1,1)
fplot3([t -t], t, [t -t])
title('Multiple Lines Using Vector Inputs')

subplot(2,1,2)
fplot3(t, t, t)
hold on
fplot3(-t, t, -t)
title('Multiple Lines Using Hold On Command')

hold off

Изменение 3-D параметрической строки после создания

Постройте параметрический график

Обеспечьте вывод, чтобы заставить fplot возвратить объект графика.

syms t
xt = exp(-abs(t)/10).*sin(5*abs(t));
yt = exp(-abs(t)/10).*cos(5*abs(t));
zt = t;
fp = fplot3(xt,yt,zt)

fp = 
  ParameterizedFunctionLine with properties:

    XFunction: [1x1 sym]
    YFunction: [1x1 sym]
    ZFunction: [1x1 sym]
        Color: [0 0.4470 0.7410]
    LineStyle: '-'
    LineWidth: 0.5000

  Show all properties

Измените область значений значений параметров к [-10 10] и цвета линии к красному при помощи свойств TRange и Color fp соответственно.

fp.TRange = [-10 10];
fp.Color = 'r';

Добавление заголовка и подписей по осям и метки деления формата

Для $$t$$ значения в области значений $$-2\pi$$ к $$2\pi$$, постройте параметрический график

Добавьте заголовок и подписи по осям. Создайте метки деления оси X путем охвата пределов оси X с промежутками в pi/2. Отобразите эти метки деления при помощи свойства XTick. Создайте метки оси X при помощи arrayfun, чтобы применить texlabel к S. Отобразите эти метки при помощи свойства XTickLabel. Повторите эти шаги для оси Y.

Чтобы использовать LATEX в графиках, смотрите latex.

syms t
xt = t;
yt = t/2;
zt = sin(6*t);
fplot3(xt,yt,zt,[-2*pi 2*pi],'MeshDensity',30)
view(52.5,30)
xlabel('x')
ylabel('y')
title('x=t, y=t/2, z=sin(6t) for -2\pi < t < 2\pi')
ax = gca;

S = sym(ax.XLim(1):pi/2:ax.XLim(2));
ax.XTick = double(S);
ax.XTickLabel = arrayfun(@texlabel, S, 'UniformOutput', false);

S = sym(ax.YLim(1):pi/2:ax.YLim(2));
ax.YTick = double(S);
ax.YTickLabel = arrayfun(@texlabel, S, 'UniformOutput', false);

Создание анимаций

Создайте анимации путем изменения отображенного выражения с помощью XFunction, YFunction и свойств ZFunction и затем при помощи drawnow, чтобы обновить график. Чтобы экспортировать в GIF, смотрите imwrite.

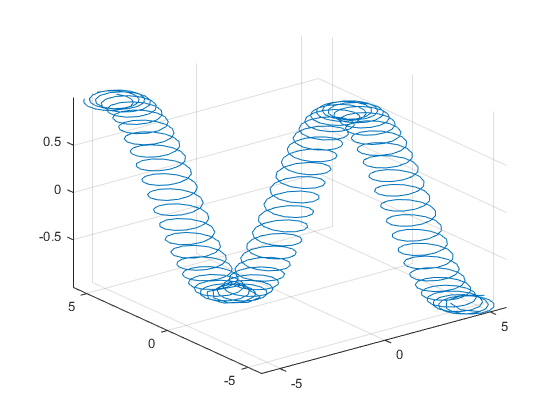
Путем варьирования переменной i от 0 до 4π, анимируйте параметрическую кривую

Чтобы проигрывать анимацию, нажмите на изображение.

syms t
fp = fplot3(t+sin(40*t),-t+cos(40*t), sin(t));
for i=0:pi/10:4*pi
    fp.ZFunction = sin(t+i);
drawnow
end