числовой::Решите линейное матричное уравнение
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
numeric::matlinsolve(A, B, options)
numeric::matlinsolve(A, B) возвращает матричное решение X матричного уравнения A X = B вместе с ядром матричного A.
numeric::matlinsolve является быстрым числовым линейным решателем и для разреженных и для плотных систем. Это - также рекомендуемый решатель для линейных систем с точными или символьными коэффициентами (используйте опцию Symbolic).
Если никакие не возвращаются, тип задан с помощью опции ReturnType = d, доменный тип данных о возврате зависит от типа входной матрицы A:
Специальное решение X, а также ядро массива A возвращено как массивы.
Специальное решение X, а также ядро hfarray A возвращено как hfarrays.
Для плотного matrixA типа Dom::DenseMatrix() оба специальное решение X, а также ядро A возвращен как матрицы типа Dom::DenseMatrix() по звонку выражений MuPAD®.
Для всех других матриц категории Cat::Matrix оба специальное решение X, а также ядро A возвращен как матрицы типа Dom::Matrix() по звонку выражений MuPAD. Это включает входные матрицы A типа Dom::Matrix(...), Dom::SquareMatrix(...), Dom::MatrixGroup(...) и т.д.
Без Symbolic, точные числовые входные данные, такие как PI + sqrt(2), sin(3) и т.д. преобразован в числа с плавающей запятой. Арифметика с плавающей точкой используется. Его точности дают переменную окружения DIGITS. Если символьные данные найдены, что это не может быть преобразовано в числа с плавающей запятой, numeric::matlinsolve автоматически переключается на свой символьный режим, выдавая предупреждение. Это предупреждение может быть подавлено через NoWarning.
С Symbolic, символьными параметрами в матрице коэффициентов A, а также в правой стороне B приняты и обработаны без предупреждения.
С SofwareFloats правая сторона B может содержать символьные параметры, которые не могут быть преобразованы в числа с плавающей запятой. Все записи матрицы коэффициентов A, однако, должны быть конвертируемыми к числам с плавающей запятой.
С HardwareFloats ни A, ни B не должны содержать символьные параметры, которые не могут быть преобразованы в числа с плавающей запятой.
X является специальным решением уравнения A X = B. Если A имеет нетривиальное ядро, решение, X не уникален.
Результат, вычисленный с HardwareFloats, может отличаться от решения, вычисленного с SoftwareFloats или Symbolic! В частности, дело обстоит так для систем с нетривиальным ядром.
Cf. Пример 9.
n ×d матричный KernelBasis является самым общим решением A X = 0. Его столбцы охватывают d - размерное ядро A.
Таким образом ядро A может быть вычислено через numeric::matlinsolve(A, [0, ..., 0])[2].
Если ядро является 0-мерным, возвращаемое значение KernelBasis является целым числом 0. Если KernelBasis возвращен как массив, размерность, d ядра является d = op(KernelBasis, [0, 3, 2]]). Если KernelBasis возвращен как матрица типа Dom::Matrix() или Dom::DenseMatrix(), размерность, d ядра является d = KernelBasis::dom::matdim(KernelBasis)[2].
Из-за ошибок округления, по некоторым или всем базисным векторам в ядре A можно скучать в числовых режимах.
Специальное решение X в сочетании с KernelBasis предоставляет общее решение A X = B. Решения сгенерировали без опции, ShowAssumptions допустим для произвольных комплексных чисел символьных параметров, которые могут присутствовать в A и B. Если никакое такое решение не существует, то [FAIL,NIL] возвращен. Решения, которые допустимы только для специальных значений символьных параметров, могут быть получены с ShowAssumptions. Смотрите Пример 3, Пример 4 и Пример 7.
numeric::matlinsolve внутренне использует разреженное представление матриц. Это подходит для решения больших разреженных систем. Смотрите Пример 5.
numeric::matlinsolve не реагирует ни на какие предположения на символьных параметрах в A,B, которые устанавливаются через assume.
Исключение Гаусса с частичным поворотом используется. Без опции Symbolic вертящаяся стратегия заботится о числовой стабилизации. С Symbolic приняты точные данные. Символьные вертящиеся попытки стратегии максимизируют скорость, и не заботится о числовой стабилизации! Не используйте Symbolic для линейных систем, включающих записи с плавающей точкой! Смотрите Пример 6.
Кроме матриц типа Dom::Matrix(...), Cat::Matrix возражает A от матричных областей, таких как Dom::DenseMatrix (...) или Dom::SquareMatrix, (...) внутренне преобразован в массивы по выражениям через expr(A). Обратите внимание на то, что Symbolic опции должен использоваться, если записи не могут быть преобразованы в числовые выражения.
Обратите внимание на то, что linalg::matlinsolve должен использоваться, когда решение состоит в том, чтобы быть вычислено по области компонента. Смотрите. Пример 8.
Без опции Symbolic функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Мы используем эквивалентные форматы ввода (B1, B2), чтобы представлять вектор с компонентами [a, π]. Во-первых, этот вектор задан как 2-мерный массив:
A := array(1..2, 1..3, [[1, 2, 3],[1, 1, 2]]): B1 := array(1..2, 1..1, [[a], [PI]]): numeric::matlinsolve(A, B1)

Затем, мы используем 1-мерный массив и вычисляем точное решение:
B2 := array(1..2, [a, PI]): numeric::matlinsolve(A, B2, Symbolic)

Теперь, список используется, чтобы задать вектор. Никакие внутренние предположения не использовались numeric::matlinsolve, чтобы получить решение:
B3 := [a, PI]: numeric::matlinsolve(A, B3, ShowAssumptions)
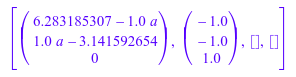
Наконец, мы используем объекты Dom::Matrix задать систему. Обратите внимание на то, что результаты возвращены, когда соответствующая матрица возражает:
A := matrix([[1, 2, 3],[1, 1, 2]]): B4 := matrix([a, PI]): numeric::matlinsolve(A, B4)

delete A, B1, B2, B3, B4:
Мы инвертируем матрицу путем решения A X = 1:
A := hfarray(1..3, 1..3, [[1, 1, 0], [0, 1, 1], [0, 0, 1]]): B := matrix::identity(3, 3): InverseOfA := numeric::matlinsolve(A, B, Symbolic)[1]

delete A, B, InverseOfA:
Мы решаем уравнение с символьным параметром x:
A := matrix([[2, 2, 3], [1, 1, 2], [3, 3, 5]]): B := matrix([sin(x)^2, cos(x)^2, 0]): [X, Kernel, Constraints, Pivots] := numeric::matlinsolve(A, B, Symbolic, ShowAssumptions)

Это решение содержит подвергающийся ограничению sin (x) 2 + cos (x) 2 = 0 на параметре x. numeric::matlinsolve не исследует Constraints и не понимает, что они не могут быть удовлетворены. Мы проверяем непротиворечивость “результата” путем вставки решения в исходную систему. Начиная с входной матрицы A имел тип Dom::Matrix(), результаты, X и Kernel были возвращены как соответствующие матрицы. Перегруженные операторы * и - для умножения матриц и вычитания могут использоваться:
A*X - B, A*Kernel
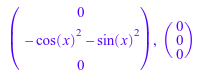
delete A, B, X, Kernel, Constraints, Pivots:
Мы даем дальнейшую демонстрацию опции ShowAssumptions. Следующая система не имеет решения для всех значений параметра a:
A := array(1..2, 1..2, [[1, 1], [1, 1]]): B := array(1..2, 1..1, [[1], [a]]): numeric::matlinsolve(A, B, Symbolic)
![]()
С ShowAssumptions numeric::matlinsolve занимается расследованиями под который условия (на параметре a) существует решение:
numeric::matlinsolve(A, B, Symbolic, ShowAssumptions)
![]()
Мы приходим к заключению, что существует 1-мерный пробел решения для a = 1.
delete A, B:
Мы решаем разреженную систему с 3 диагональными полосами:
n := 100: A := matrix(n, n, [1, -2, 1], Banded): B := array(1..n, [1 $ n]): numeric::matlinsolve(A, B)

delete n, A, B:
Symbolic опции не должен использоваться для уравнений с коэффициентами с плавающей точкой, потому что символьная вертящаяся стратегия способствует эффективности вместо числовой устойчивости.
A := array(1..2, 1..2, [[1, 10^20], [1, 1]]): B := array(1..2, 1..1, [[10^20], [0]]):
Приближение плавающее точного решения:
map(numeric::matlinsolve(A, B, Symbolic)[1], float)
![]()
Мы теперь преобразовываем точные входные данные в приближения с плавающей точкой:
A := map(A, float): B := map(B, float):
Значение по умолчанию, вертящееся стратегия алгоритма с плавающей точкой, стабилизирует операции с плавающей точкой. Следовательно, каждый получает правильный результат:
numeric::matlinsolve(A, B)[1]
![]()
С опцией Symbolic, однако, вертящаяся стратегия оптимизирует скорость, принимая точную арифметику. Числовая нестабильность может произойти, если коэффициенты с плавающей точкой включены. Следующий результат вызывается внутренними эффектами округления (“отмена”):
numeric::matlinsolve(A, B, Symbolic)[1]
![]()
Мы должны увеличить DIGITS, чтобы получить лучший результат:
DIGITS := 20: numeric::matlinsolve(A, B, Symbolic)[1]
![]()
delete A, B, DIGITS:
Мы демонстрируем, как полное решение следующей линейной системы с символьными параметрами может быть найдено:
A := array(1..3, 1..2, [[1, 1], [a, b], [1, c]]): B := array(1..3, 1..1, [[1], [1], [1]]): numeric::matlinsolve(A, B, Symbolic, ShowAssumptions)

Это - общее решение, принимающее a ≠ b. Мы теперь устанавливаем b = a исследовать дальнейшие ответвления решения:
A := subs(A, b = a): numeric::matlinsolve(A, B, Symbolic, ShowAssumptions)
![]()
Это - общее решение для a = b, принимая c ≠ 1. Мы наконец устанавливаем c = 1 получать последнее ответвление решения:
A := subs(A, c = 1): numeric::matlinsolve(A, B, Symbolic, ShowAssumptions)
![]()
От ограничения на a мы приходим к заключению, что существует 1-мерный пробел решения для специальных значений a = b = c = 1 из символьных параметров.
delete A, B:
Матрицы от области, такие как Dom::Matrix (...) преобразованы в массивы с числами или выражениями. Следовательно, numeric::matlinsolve не находит решения для следующей системы:
M := Dom::Matrix(Dom::IntegerMod(7)): A := M([[1, 4], [6, 3], [3, 2]]): B := M([[9], [5], [0]]): numeric::matlinsolve(A, B)
![]()
Используйте linalg::matlinsolve, чтобы решить систему по содействующему полю матриц. Решение действительно существует по полю Dom::IntegerMod (7):
linalg::matlinsolve(A, B)

delete M, A, B:
Мы демонстрируем различие между Symbolic, HardwareFloats и SoftwareFloats. Следующий матричный A имеет 1-мерное ядро. Из-за округления, дальнейший побочный вектор ядра появляется с SoftwareFloats. Никакой вектор ядра не обнаруживается с HardwareFloats:
A := matrix([[2*10^14 + 2, 2*10^(-9), 2*10^(-4)],
[3*10^15 + 3, 3*10^(-8), 3*10^(-3)],
[4*10^16 + 4, 4*10^(-7), 4*10^(-2)]
]):
b := matrix([2*10^(-9), 3*10^(-8), 4*10^(-7)]):
float(numeric::matlinsolve(A, b, Symbolic));
numeric::matlinsolve(A, b, SoftwareFloats);
numeric::matlinsolve(A, b, HardwareFloats)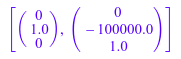
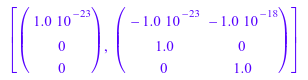

delete A, b:
|
m ×n матрица доменный тип |
|
m ×p матрица доменного типа |
|
С С По сравнению с Если никакой Если результат не может быть вычислен с аппаратными плаваниями, арифметику программного обеспечения ядром MuPAD пробуют. Если текущее значение Может быть несколько причин аппаратной арифметики, чтобы перестать работать:
Если ни Если Обратите внимание на то, что Запаздывающие цифры в результатах с плавающей точкой, вычисленных с ПримечаниеДля плохо обусловленных матриц результаты, возвращенные с |
|
Предотвращает преобразование входных данных к числам с плавающей запятой. Точная арифметика используется. Эта опция заменяет Эта опция должна использоваться, если матричный A содержит символьные параметры, которые не могут быть преобразованы в числа с плавающей запятой. ПримечаниеЭта опция не должна использоваться для матриц с записями с плавающей точкой! Числовая нестабильность может произойти в операциях с плавающей точкой. Cf. Пример 6. |
|
Возвращает информацию о внутренних предположениях на символьных параметрах в Эта опция только полезна, если матрицы содержат символьные параметры. Следовательно, это должно только использоваться в сочетании с опцией ПримечаниеЭта опция изменяет формат возвращаемого значения к
Такие ограничения возникают, если Исключение Гаусса приводит к уравнениям формы 0 = c, где c является некоторым выражением, включающим символьные параметры, содержавшиеся в B. Все такие уравнения собраны в Если никакие такие ограничения не возникают, возвращаемое значение
Примечание
ПримечаниеЭта опция изменяет стратегию возврата “неразрешимых” систем. Без опции |
|
Отключает предупреждения Если символьные коэффициенты найдены, |
|
Опция, заданная как Возвратите (специальное) решение и ядро как матрицы доменного типа |
|
Используйте разреженное внутреннее представление для матриц. Эта опция только имеет эффект, когда используется в сочетании с |
Без опции ShowAssumptions список возвращен [X, KernelBasis]. (Специальным) решением X является n ×p матрица. KernelBasis является n ×d матрица (d является размерностью ядра A). Его столбцы охватывают ядро A. Если ядро тривиально, KernelBasis является целым числом 0.
[FAIL, NIL] возвращен, если система не разрешима.
С ShowAssumptions список возвращен [X, KernelBasis, Constraints, Pivots]. Списки Constraints и Pivots содержат уравнения и неравенства, вовлекающие символьные параметры в A и B. Внутренне они были приняты, чтобы сохраняться при решении системы. [FAIL, NIL, [], []] возвращен, если система не разрешима.