график::Потоки векторных полей
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
plot::Streamlines2d([v1, v2],x = xmin .. xmax,y = ymin .. ymax, <a = amin .. amax>,options) plot::Streamlines2d(v1,v2,x = xmin .. xmax,y = ymin .. ymax, <a = amin .. amax>,options) plot::Streamlines2d(V,x = xmin .. xmax,y = ymin .. ymax, <a = amin .. amax>,options)
plot::Streamlines2d( [v1, v2] , x = `x_{min}`..`x_{max}` , y = `y_{min}`..`y_{max}` ) создает потоки векторного поля, заданного![]() с (x, y) ∈ [x min, x max] × [y min, y max].
с (x, y) ∈ [x min, x max] × [y min, y max].
Векторное поле задано функцией![]() .
. plot::Streamlines2d отображает векторное поле путем рисования почти равномерно распределенных потоков векторного поля, т.е. изгибается, к которому векторное поле является тангенциальным в каждой точке. Плотностью линий потоков (и время, необходимое для вычисления), управляют с атрибутом MinimumDistance.
Как показывает опыт: уменьшение значения MinimumDistance фактором 2 приводит к увеличению времени выполнения фактором 4.
Схема определяемого пользователем цвета может быть задана LineColorFunction = color, где color является процедурой MuPAD®, принимающей 6 входных параметров и возвращающей список значений RGB. Во время графического вывода эта функция вызвана в форме color(x, y, v1, v2, t, l, n):
Значения x, y является координатами текущей точки.
Значения v1, v2 является компонентами векторного поля в текущей точке.
Значение t является “временем” текущей точки (x, y) на текущем потоке. Масштабирование этого параметра зависит от векторного поля.
Значение l является длиной кривой текущего потока от его отправной точки текущая точка (x, y) как Евклидово расстояние. Этот параметр является инвариантным относительно скалярных изменений векторного поля (до изменения направления потока).
Целочисленное значение n является количеством текущего потока. Каждый отдельный поток имеет различное значение.
Cf. Пример 3.
| Атрибут | Цель | Значение по умолчанию |
|---|---|---|
AbsoluteError | максимальная абсолютная ошибка дискретизации | |
AffectViewingBox | влияние объектов на ViewingBox сцены | TRUE |
AntiAliased | сглаженные строки и точки? | TRUE |
Frames | количество кадров в анимации | 50 |
Legend | делает запись легенды | |
LegendText | короткий объяснительный текст для легенды | |
LegendEntry | добавить этот объект в легенду? | FALSE |
LineColor | цвет строк | RGB::Black |
LineWidth | ширина строк | 0.35*unit::mm |
LineColor2 | цвет строк | RGB::DeepPink |
LineStyle | тело, подчеркнутые штриховой линией или пунктирные линии? | Solid |
LineColorType | типы окраски строки | Flat |
LineColorFunction | функциональная окраска строки | |
MinimumDistance | пробел между линиями потоков | |
Name | имя объекта графика (для браузера и легенды) | |
ODEMethod | числовая схема, используемая для того, чтобы решить ОДУ | ABM4 |
ParameterEnd | закончите значение параметра анимации | |
ParameterName | имя параметра анимации | |
ParameterBegin | начальное значение параметра анимации | |
ParameterRange | область значений параметра анимации | |
RelativeError | максимальная относительная ошибка дискретизации | 1/100000 |
Stepsize | установите постоянный размер шага | |
TimeEnd | время окончания анимации | 10.0 |
TimeBegin | время начала анимации | 0.0 |
TimeRange | оперативный промежуток анимации | 0.0 .. 10.0 |
TipAngle | вводный угол наконечников стрелки | (2*PI)/15 |
TipStyle | стиль презентации наконечников стрелки | Filled |
TipLength | длина наконечников стрелки | 0 |
Title | объектный заголовок | |
TitleFont | шрифт объектных заголовков | [" sans-serif ", 11] |
TitlePosition | положение объектных заголовков | |
TitleAlignment | выравнивание по горизонтали заголовков w.r.t. их координаты | Center |
TitlePositionX | положение объектных заголовков, x компонент | |
TitlePositionY | положение объектных заголовков, y компонент | |
Visible | видимость | TRUE |
VisibleAfter | объект, видимый после этой временной стоимости | |
VisibleBefore | объект, видимый до этой временной стоимости | |
VisibleFromTo | объект, видимый в это время, располагается | |
VisibleAfterEnd | объект, видимый после его законченного времени анимации? | TRUE |
VisibleBeforeBegin | объект, видимый перед его временем анимации, запускается? | TRUE |
XFunction | функция для x значений | |
XMax | окончательное значение параметра “x” | |
XMin | начальное значение параметра “x” | |
XName | имя параметра “x” | |
XRange | область значений параметра “x” | |
YFunction | функция для y значений | |
YMax | окончательное значение параметра “y” | |
YMin | начальное значение параметра “y” | |
YName | имя параметра “y” | |
YRange | область значений параметра “y” |
plot::Streamlines2d изображает векторные поля (более или менее) равноотстоящими линиями потоков:
plot(plot::Streamlines2d(-x, -y, x=-2..2, y=-2..2))
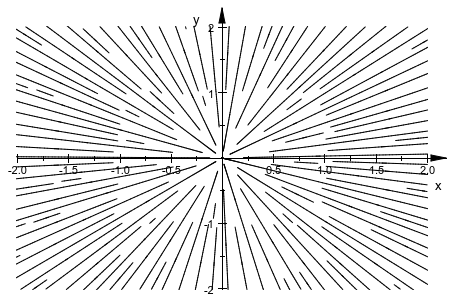
Обратите внимание на то, что этот стиль отображения обязательно повреждает симметрии, в этом случае совершенная осевая симметрия векторного поля.
Кроме того, циклы не будут закрыты, но оставят разрыв:
plot(plot::Streamlines2d(-y, x, x=-2..2, y=-2..2))
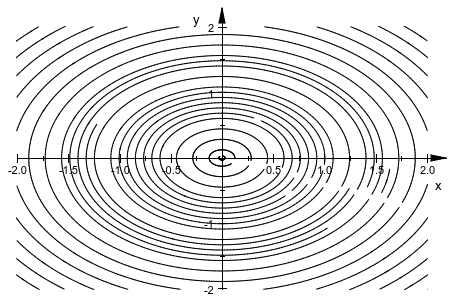
Кроме “обычных” параметров, таких как области значений параметра, цвет линии или ширина линии, plot::Streamlines2d можно управлять с атрибутом MinimumDistance, который устанавливает минимальное расстояние между линиями потоков:
plot(plot::Streamlines2d(sin(x^2+y^2), cos(x^2+y^2),
x = -3..3, y = -2..2))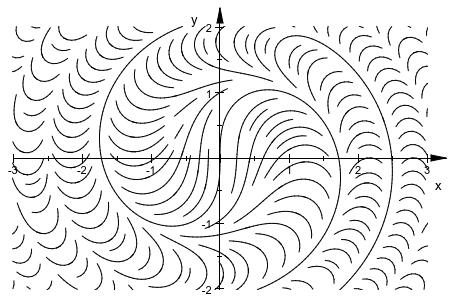
plot(plot::Streamlines2d(sin(x^2+y^2), cos(x^2+y^2),
x = -3..3, y = -2..2,
MinimumDistance = 0.2))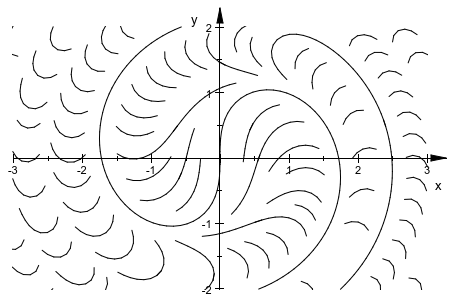
plot(plot::Streamlines2d(sin(x^2+y^2), cos(x^2+y^2),
x = -3..3, y = -2..2,
MinimumDistance = 0.05))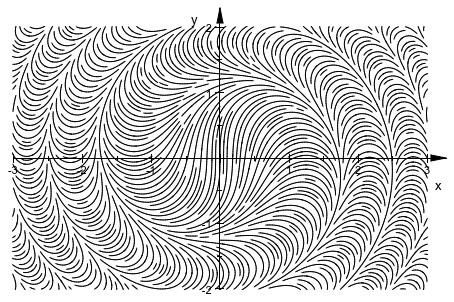
Функция цвета линии для plot::Streamlines2d имеет доступ к текущим координатам, к компонентам векторного поля в текущей точке, к текущей длине на кривой (и с точки зрения параметра “времени” и с точки зрения Евклидова расстояния) и целочисленное количество текущей кривой (которые не найдены в некотором предопределенном порядке). Мы используем номер кривой, чтобы сгенерировать красочное отображение:
num2col := (x, y, vx, vy, t, l, n) -> RGB::fromHSV([111*n, 1, 1]):
plot(plot::Streamlines2d(sin(x^2+y^2), cos(x^2+y^2),
x = -3..3, y = -2..2,
LineColorFunction = num2col))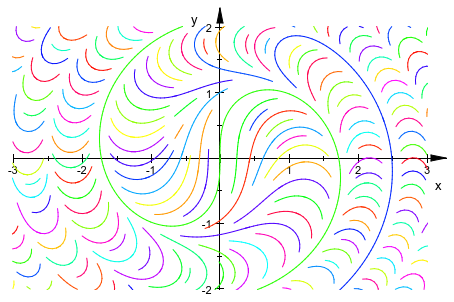
Используя кривую информация о длине позволяет нам включать направленную информацию в отображение:
l2col := (x, y, vx, vy, t, l) -> [frac(5*l) $ 3]:
plot(plot::Streamlines2d(sin(x^2+y^2), cos(x^2+y^2),
x = -3..3, y = -2..2,
LineWidth = 0.75,
LineColorFunction = l2col))
Часто, более легкий способ построить ориентацию линий потоков состоит в том, чтобы активировать наконечники стрелки графики plot::Streamlines2d в середину каждого достаточно долго), линия потоков. Они сделаны невидимыми длиной совета по умолчанию 0:
plot(plot::Streamlines2d(0.3*x-y, 0.3*y+x,
x = -3..3, y = -2..2,
TipLength = 3*unit::mm))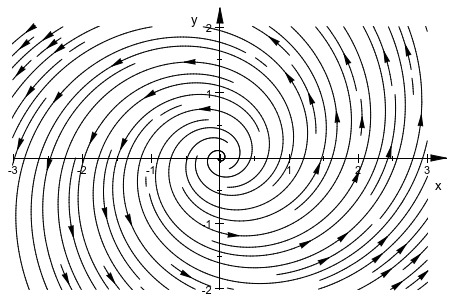
Поскольку размещение линий потоков трудно предсказать, plot::Streamlines2d не действительно подходит для анимаций. Возможно анимировать plot::Streamlines2d, но когерентность между кадрами анимации меньше чем обычно:
plot(plot::Streamlines2d(sin(x^2+y^2), cos(x^2-y^2+a),
x = -2..2, y = -2..2, a = -PI..PI,
MinimumDistance = 0.1,
Frames=10))
С настройками по умолчанию plot::Streamlines2d не может построить векторное поле![]() (который не является непрерывным Липшицом) удовлетворяющим способом:
(который не является непрерывным Липшицом) удовлетворяющим способом:
plot(plot::Streamlines2d([1, surd(3,y)^2],
x=-3..3, y=-2..2))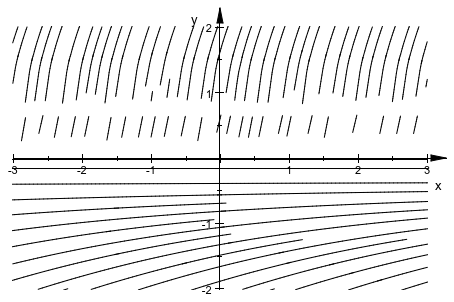
При помощи различного числового интегратора проблемы могут быть преодолены (за счет более длительного вычисления):
plot(plot::Streamlines2d([1, surd(3,y)^2],
x=-3..3, y=-2..2,
ODEMethod=RKF43,
RelativeError=1e-3))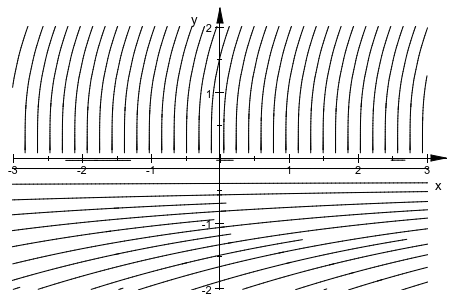
|
x - и y - компонент векторного поля: арифметические выражения в |
|
Матрица категории |
|
Идентификаторы. |
|
Действительные численные значения.
|
|
Параметр анимации, заданный как |
Алгоритм, используемый в plot::Streamlines2d, был опубликован в “Создании Равномерно распределенных Потоков Произвольной Плотности” Бруно Джобардом и Уилфридом Лефером на Еврографическом Семинаре в Boulogne-sur-Mer, Франция.