Оцените и подтвердите линейные модели от multiple-input/single-output (MISO) данные, чтобы найти тот, который лучше всего описывает системную динамику.
После завершения этого примера вы сможете выполнить следующие задачи с помощью командной строки:
Создайте объекты данных представлять данные.
Отобразите данные на графике.
Обработайте данные путем удаления смещений из сигналов ввода и вывода.
Оцените и подтвердите линейные модели из данных.
Симулируйте и предскажите выход модели.
Этот пример использует данные временного интервала, чтобы продемонстрировать, как можно оценить линейные модели. Тот же рабочий процесс применяется к подходящим данным частотного диапазона.
Этот пример использует файл данных co2data.mat, который содержит два эксперимента 2D входа и одно выход (MISO) данные временного интервала из установившегося, которое оператор встревожил от значений равновесия.
В первом эксперименте оператор ввел импульсную волну обоим входным параметрам. Во втором эксперименте оператор ввел импульсную волну первому входу и сигнал шага к второму входу.
Загрузите данные.
load co2data
Эта команда загружает следующие пять переменных в рабочее пространство MATLAB:
Input_exp1 и Output_exp1 входные и выходные данные из первого эксперимента, соответственно.
Input_exp2 и Output_exp2 входные и выходные данные из второго эксперимента, соответственно.
Time временной вектор от 0 до 1 000 минут, увеличивающихся с равным шагом 0.5 min.
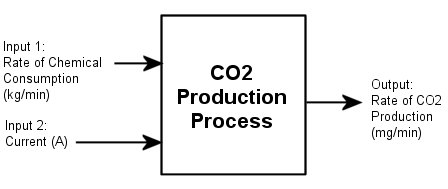
Для обоих экспериментов входные данные состоят из двух столбцов значений. Первый столбец значений является уровнем химического потребления (в килограммах в минуту), и второй столбец значений является током (в амперах). Выходные данные являются отдельным столбцом уровня производства углекислого газа (в миллиграммах в минуту).
Постройте входные и выходные данные из обоих экспериментов.
plot(Time,Input_exp1,Time,Output_exp1) legend('Input 1','Input 2','Output 1') figure plot(Time,Input_exp2,Time,Output_exp2) legend('Input 1','Input 2','Output 1')


Первый график показывает первый эксперимент, где оператор применяет импульсную волну к каждому входу, чтобы встревожить его от его установившегося равновесия.
Второй график показывает второй эксперимент, где оператор применяет импульсную волну к первому входу и сигнал шага к второму входу.
Отображение на графике данных, как описано в Отображении на графике Данных о вводе/выводе, показывает, что входные параметры и выходные параметры имеют ненулевые значения равновесия. В этом фрагменте примера вы вычитаете значения равновесия из данных.
Причина вы вычитаете средние значения из каждого сигнала, состоит в том, потому что, обычно, вы создаете линейные модели, которые описывают ответы для отклонений от физического равновесия. С установившимися данными разумно принять, что средние уровни сигналов соответствуют такому равновесию. Таким образом можно искать модели вокруг нуля, не моделируя абсолютные уровни равновесия в физических единицах измерения.
Увеличьте масштаб графиков видеть, что самый ранний момент, когда оператор применяет воздействие к входным параметрам, происходит после 25 минут установившихся условий (или после первых 50 выборок). Таким образом среднее значение первых 50 выборок представляет условия равновесия.
Используйте следующие команды, чтобы удалить значения равновесия из вводов и выводов в обоих экспериментах:
Input_exp1 = Input_exp1-... ones(size(Input_exp1,1),1)*mean(Input_exp1(1:50,:)); Output_exp1 = Output_exp1-... mean(Output_exp1(1:50,:)); Input_exp2 = Input_exp2-... ones(size(Input_exp2,1),1)*mean(Input_exp2(1:50,:)); Output_exp2 = Output_exp2-... mean(Output_exp2(1:50,:));
Объекты данных System Identification Toolbox™, iddata и idfrd, инкапсулируйте значения данных и свойства данных в одну сущность. Можно использовать команды System Identification Toolbox, чтобы удобно управлять этими объектами данных как одна сущности.
В этом фрагменте примера вы создаете два iddata объекты, один для каждого из двух экспериментов. Вы используете данные из Эксперимента 1 для оценки модели и данные из Эксперимента 2 для проверки допустимости модели. Вы работаете с двумя независимыми наборами данных, потому что вы используете один набор данных в оценке модели и другой для проверки допустимости модели.
Когда два независимых набора данных не доступны, можно разделить один набор данных в две части, приняв, что каждая часть содержит достаточно информации, чтобы соответственно представлять системную динамику.
Вы, должно быть, уже загрузили выборочные данные в рабочую область MATLAB®, как описано в Загрузке Данных в рабочее пространство MATLAB.
Используйте эти команды, чтобы создать два объекта данных, ze и zv :
Ts = 0.5; % Sample time is 0.5 min
ze = iddata(Output_exp1,Input_exp1,Ts);
zv = iddata(Output_exp2,Input_exp2,Ts);
ze содержит данные из Эксперимента 1 и zv содержит данные из Эксперимента 2. Ts шаг расчета.
iddata конструктор требует трех аргументов для данных временного интервала и имеет следующий синтаксис:
data_obj = iddata(output,input,sampling_interval);
Просмотреть свойства iddata объект, используйте get команда. Например, введите эту команду, чтобы получить свойства данных об оценке:
get(ze)
ans =
struct with fields:
Domain: 'Time'
Name: ''
OutputData: [2001x1 double]
y: 'Same as OutputData'
OutputName: {'y1'}
OutputUnit: {''}
InputData: [2001x2 double]
u: 'Same as InputData'
InputName: {2x1 cell}
InputUnit: {2x1 cell}
Period: [2x1 double]
InterSample: {2x1 cell}
Ts: 0.5000
Tstart: []
SamplingInstants: [2001x0 double]
TimeUnit: 'seconds'
ExperimentName: 'Exp1'
Notes: {}
UserData: []
Чтобы узнать больше о свойствах этого объекта данных, смотрите iddata страница с описанием.
Чтобы изменить свойства данных, можно использовать запись через точку или set команда. Например, чтобы присвоить названия канала и модули, которые подписывают оси графика, введите следующий синтаксис в Окне Команды MATLAB:
% Set time units to minutes ze.TimeUnit = 'min'; % Set names of input channels ze.InputName = {'ConsumptionRate','Current'}; % Set units for input variables ze.InputUnit = {'kg/min','A'}; % Set name of output channel ze.OutputName = 'Production'; % Set unit of output channel ze.OutputUnit = 'mg/min'; % Set validation data properties zv.TimeUnit = 'min'; zv.InputName = {'ConsumptionRate','Current'}; zv.InputUnit = {'kg/min','A'}; zv.OutputName = 'Production'; zv.OutputUnit = 'mg/min';
Можно проверить что InputName свойство ze изменяется, или "индекс" в это свойство:
ze.inputname;
Имена свойства, такие как InputUnit, не являются чувствительными к регистру. Можно также сократить имена свойства, которые запускаются с Input или Output путем замены u для Input и y для Output на имя свойства. Например, OutputUnit эквивалентно yunit.
Можно построить iddata объекты с помощью plot команда.
Отобразите данные об оценке на графике.
plot(ze)

Нижние оси показывают входным параметрам ConsumptionRate и Current, и главные оси показывают выход ProductionRate .
Отобразите данные о валидации на графике в новом окне рисунка.
figure % Open a new MATLAB Figure window plot(zv) % Plot the validation data

Увеличьте масштаб графиков видеть, что процесс эксперимента усиливает первый вход (ConsumptionRate ) фактором 2, и усиливает второй вход (Current ) фактором 10.
Прежде чем вы начнете, создадите новый набор данных, который содержит только первые 1 000 выборок исходных наборов данных оценки и валидации, чтобы ускорить вычисления.
Ze1 = ze(1:1000); Zv1 = zv(1:1000);
Для получения дополнительной информации об индексации в iddata объекты, смотрите соответствующую страницу с описанием.
Частотная характеристика и переходной процесс являются непараметрическими моделями, которые могут помочь вам изучить динамические характеристики своей системы. Эти модели не представлены компактной математической формулой корректируемыми параметрами. Вместо этого они состоят из таблиц данных.
В этом фрагменте примера вы оцениваете эти модели с помощью набора данных ze. Вы, должно быть, уже создали ze, как описано в Создании iddata Объекты.
Графики отклика из этих моделей показывают следующие характеристики системы:
Ответ от первого входа до выхода может быть функцией второго порядка.
Ответ от второго входа до выхода может быть первым порядком или сверхослабленной функцией.
Продукт System Identification Toolbox обеспечивает три функции для оценки частотной характеристики:
Используйте spa оценить частотную характеристику.
Ge = spa(ze);
Постройте частотную характеристику как Диаграмму Боде.
bode(Ge)

Амплитуда достигает максимума на частоте 0,54 рад/min, которые предлагают возможное резонирующее поведение (комплексные полюса) для первой комбинации входа к выходу - ConsumptionRate к Production .
В обоих графиках фаза прокручивается прочь быстро, который предлагает задержку обеих комбинаций ввода/вывода.
Чтобы оценить переходной процесс из данных, сначала оцените непараметрическую модель импульсной характеристики (КИХ-фильтр) из данных и затем постройте его переходной процесс.
% model estimation Mimp = impulseest(Ze1,60); % step response step(Mimp)

Переходной процесс для первой комбинации ввода/вывода предлагает перерегулирование, которое указывает на присутствие underdamped режима (комплексные полюса) в физической системе.
Переходной процесс от второго входа до выхода не показывает перерегулирования, которое указывает или на ответ первого порядка или на ответ высшего порядка с действительными полюсами (сверхослабленный ответ).
Переходный процесс указывает на ненулевую задержку системы, которая сопоставима с быстрым спадом фазы, вы вошли в Диаграмму Боде, которую вы создали в Оценке Эмпирического Переходного процесса.
Чтобы идентифицировать параметрические модели черного ящика, необходимо задать задержку ввода/вывода как часть порядка модели.
Если вы не знаете задержки ввода/вывода своей системы из эксперимента, можно использовать программное обеспечение System Identification Toolbox, чтобы оценить задержку.
В случае систем одно входа можно считать задержку на графике импульсной характеристики. Однако в случае нескольких - входные системы, такие как та в этом примере, вы можете не мочь сказать, которые вводят, вызвал начальное изменение в выходе, и можно использовать delayest команда вместо этого.
Команда оценивает задержку динамической системы путем оценки младшего разряда, модели ARX дискретного времени с областью значений задержек, и затем выбора задержки что, соответствуя лучшей подгонке.
Структура модели ARX является одним из самого простого черного ящика параметрические структуры. В дискретное время структура ARX является разностным уравнением со следующей формой:
y (t) представляет выход во время t, u (t) представляет вход во время t, na является количеством полюсов, nb является количеством b параметров (равный количеству нулей плюс 1), nk является количеством выборок, прежде чем вход будет влиять на выход системы (названный задержкой или потеря времени модели), и e (t) является бело-шумовым воздействием.
delayest принимает это na=nb=2 и что шум e является белым или незначительным, и оценивает nk.
Чтобы оценить задержку этой системы, введите:
delayest(ze)
ans =
5 10
Этот результат включает два числа, потому что существует два входных параметров: предполагаемой задержкой первого входа является 5 выборками данных и предполагаемой задержкой второго входа является 10 выборки данных. Поскольку шагом расчета для экспериментов является 0.5 min, это соответствует 2.5 - задержка min перед первым входом влияет на выход и 5.0 - задержка min перед вторым входом влияет на выход.
Существует два альтернативных метода для оценки задержки системы:
Постройте график временной зависимости входных и выходных данных и считайте разницу во времени между первым изменением во входе и первым изменением в выходе. Этот метод практичен только для single-input/single-output системы; в случае нескольких - входные системы, вы можете не мочь сказать, которые вводят, вызвал начальное изменение в выходе.
Постройте импульсную характеристику данных с областью уверенности с 1 стандартным отклонением. Можно оценить задержку с помощью времени, когда импульсная характеристика сначала за пределами области уверенности.
Порядок модели является одним или несколькими целыми числами, которые задают сложность модели. В общем случае порядок модели связан с количеством полюсов, количеством нулей и задержкой ответа (время в терминах количества выборок, прежде чем выход ответит на вход). Определенное значение порядка модели зависит от структуры модели.
Чтобы вычислить параметрические модели черного ящика, необходимо обеспечить порядок модели как вход. Если вы не знаете порядка своей системы, можно оценить его.
После завершения шагов в этом разделе вы получаете следующие результаты:
Для первой комбинации ввода/вывода: na=2, nb=2, и задержка nk=5.
Для второй комбинации ввода/вывода: na=1, nb=1, и задержка nk=10.
Позже, вы исследуете различные структуры модели путем определения стоимостей заказов модели, которые являются небольшими изменениями вокруг них первоначальная оценка.
В этом фрагменте примера вы используете struc, arxstruc, и selstruc оценить и сравнить простые полиномиальные модели (ARX) для области значений порядков модели и задержек, и выбрать лучшие порядки на основе качества модели.
Следующий список описывает результаты использования каждой команды:
struc создает матрицу комбинаций порядка модели для заданной области na, nb, и nk значения.
arxstruc берет выход из struc, систематически оценивает модель ARX для каждого порядка модели и сравнивает выход модели с измеренным выходом. arxstruc возвращает функцию потерь для каждой модели, которая является нормированной суммой ошибок прогноза в квадрате.
selstruc берет выход из arxstruc и открывает окно ARX Model Structure Selection, которое напоминает следующую фигуру, чтобы помочь вам выбрать порядок модели.
Вы используете этот график выбрать хорошо-подходящую модель.
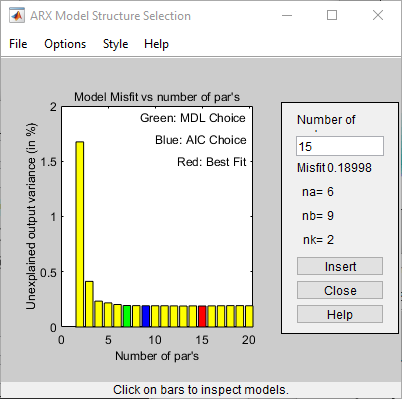
Горизонтальная ось является общим количеством параметров — na + nb.
Вертикальная ось, названная Unexplained output variance (in %), является фрагментом выхода, не объясненного моделью — ошибка прогноза модели ARX для количества параметров, показанных на горизонтальной оси.
Ошибка прогноза является суммой квадратов различий между выводом данных валидации и моделью "один шаг вперед" предсказанный выход.
nk является задержкой.
Три прямоугольника подсвечены на графике в зеленом, синем цвете, и красные. Каждый цвет указывает на тип хорошо-подходящего критерия, можно следующим образом:
Красный — Лучшая подгонка минимизирует сумму квадратов различия между выводом данных валидации и выходом модели. Этот прямоугольник указывает на полную лучшую подгонку.
Зеленый — Лучшая подгонка минимизирует критерий Rissanen MDL.
Синий — Лучшая подгонка минимизирует критерий AIC Akaike.
В этом примере значение Unexplained output variance (in %) остается приблизительно постоянным для объединенного количества параметров от 4 до 20. Такое постоянство указывает, что производительность модели не улучшается в высших порядках. Таким образом модели младшего разряда могут соответствовать данным одинаково хорошо.
Когда вы будете использовать тот же набор данных в оценке и валидации, используйте MDL и критерии AIC, чтобы выбрать порядки модели. Эти критерии компенсируют сверхподбор кривой, который следует из использования слишком многих параметров. Для получения дополнительной информации об этих критериях, смотрите selstruc страница с описанием.
В этом примере существует два входных параметров к системе и один выход, и вы оцениваете порядки модели для каждой комбинации ввода/вывода независимо. Можно или оценить задержки от двух входных параметров одновременно или одного входа за один раз.
Это целесообразно пробовать комбинации следующего заказа за первую комбинацию ввода/вывода:
na=2:5
nb=1:5
nk=5
Это вызвано тем, что непараметрические модели, которые вы оценили в Оценке Моделей Импульсной характеристики, показывают, что ответ для первой комбинации ввода/вывода может иметь ответ второго порядка. Точно так же в Оценке Задержек Нескольких - Входная Система, задержка этой комбинации ввода/вывода, как оценивалось, была 5.
Оценить порядок модели для первой комбинации ввода/вывода:
Используйте struc создать матрицу возможных порядков модели.
NN1 = struc(2:5,1:5,5);
Используйте selstruc вычислить функции потерь для моделей ARX с порядками в NN1.
selstruc(arxstruc(ze(:,:,1),zv(:,:,1),NN1))
ze(:,:,1) выбирает первый вход в данных.
Эта команда открывает интерактивное окно ARX Model Structure Selection.
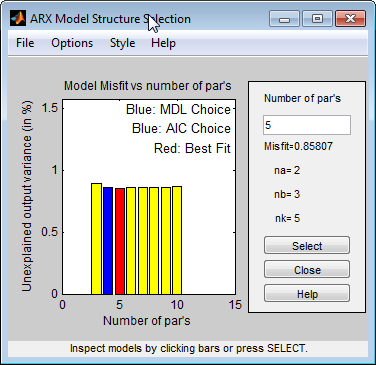
Rissanen MDL и критерии AIC Akaike приводят к эквивалентным результатам и оба обозначаются синим прямоугольником на графике.
Красный прямоугольник представляет лучшую полную подгонку, которая происходит для na=2, nb=3, и nk=5. Разность высот между красными и синими прямоугольниками незначительна. Поэтому можно выбрать комбинацию параметра, которая соответствует самому низкому порядку модели и самой простой модели.
Кликните по синему прямоугольнику, и затем нажмите Select, чтобы выбрать ту комбинацию порядков:
na=2
nb=2
nk=5
Чтобы продолжиться, нажмите любую клавишу в то время как в Окне Команды MATLAB.
Это целесообразно пробовать комбинации следующего заказа за вторую комбинацию ввода/вывода:
na=1:3
nb=1:3
nk=10
Это вызвано тем, что непараметрические модели, которые вы оценили в Оценке Моделей Импульсной характеристики, показывают, что ответ для второй комбинации ввода/вывода может иметь ответ первого порядка. Точно так же в Оценке Задержек Нескольких - Входная Система, задержка этой комбинации ввода/вывода, как оценивалось, была 10.
Оценить порядок модели для второй комбинации ввода/вывода:
Используйте struc создать матрицу возможных порядков модели.
NN2 = struc(1:3,1:3,10);
Используйте selstruc вычислить функции потерь для моделей ARX с порядками в NN2.
selstruc(arxstruc(ze(:,:,2),zv(:,:,2),NN2))
Эта команда открывает интерактивное окно ARX Model Structure Selection.
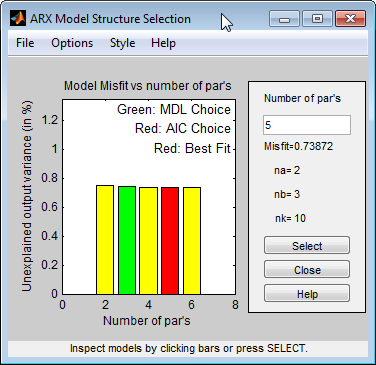
AIC Akaike и полные лучшие подходящие критерии приводят к эквивалентным результатам. Оба обозначаются тем же красным прямоугольником на графике.
Разность высот между всеми прямоугольниками незначительна и все эти порядки модели результат в подобной производительности модели. Поэтому можно выбрать комбинацию параметра, которая соответствует самому низкому порядку модели и самой простой модели.
Кликните по желтому прямоугольнику на крайне левом, и затем нажмите Select, чтобы выбрать самое низкоуровневое: na=1, nb=1, и nk=10.
Чтобы продолжиться, нажмите любую клавишу в то время как в Окне Команды MATLAB.
В этом фрагменте примера вы оцениваете передаточную функцию непрерывного времени. Вы, должно быть, уже подготовили свои данные, как описано в Подготовка данных. Можно использовать следующие результаты предполагаемых порядков модели задать порядки модели:
Для первой комбинации ввода/вывода используйте:
Два полюса, соответствуя na=2 в модели ARX.
Задержка 5, соответствуя nk=5 выборки (или 2,5 минуты) в модели ARX.
Для второй комбинации ввода/вывода используйте:
Один полюс, соответствуя na=1 в модели ARX
Задержка 10, соответствуя nk=10 выборки (или 5 минут) в модели ARX.
Можно оценить передаточную функцию этих порядков с помощью tfest команда. Для оценки можно также принять решение просмотреть отчет о выполнении работ путем установки Display опция к on в наборе опции, созданном tfestOptions команда.
Opt = tfestOptions('Display','on');
Соберите порядки модели и задержки в переменные, чтобы передать tfest.
np = [2 1]; ioDelay = [2.5 5];
Оцените передаточную функцию.
mtf = tfest(Ze1,np,[],ioDelay,Opt);
Просмотрите коэффициенты модели.
mtf
mtf =
From input "ConsumptionRate" to output "Production":
72.13 s - 1.252
exp(-2.5*s) * ----------------------
s^2 + 25.57 s + 0.9572
From input "Current" to output "Production":
5.234
exp(-5*s) * ----------
s + 0.5132
Continuous-time identified transfer function.
Parameterization:
Number of poles: [2 1] Number of zeros: [1 0]
Number of free coefficients: 6
Use "tfdata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using TFEST on time domain data "Ze1".
Fit to estimation data: 85.72%
FPE: 6.523, MSE: 6.407
Отображение модели показывает больше чем 85%-ю подгонку к данным об оценке.
В этом фрагменте примера вы создаете график, который сравнивает фактический выход и выход модели с помощью compare команда.
compare(Zv1,mtf)

Сравнение показывает приблизительно 60%-ю подгонку.
Используйте resid команда, чтобы оценить характеристики остаточных значений.
resid(Zv1,mtf)

Остаточные значения показывают высокую степень автокорреляции. Это не неожиданно начиная с модели mtf не имеет никаких компонентов, чтобы описать природу шума отдельно. Чтобы смоделировать и измеренную динамику ввода - вывода и динамику воздействия, необходимо будет использовать структуру модели, которая содержит элементы, чтобы описать шумовой компонент. Можно использовать bj, ssest и procest команды, которые создают модели полинома, пространства состояний и структур процесса соответственно. Эти структуры, среди других, содержат элементы, чтобы получить шумовое поведение.
В этом фрагменте примера вы оцениваете младший разряд, передаточная функция непрерывного времени (модель процесса). модели непрерывного времени поддержки продукта System Identification Toolbox с самое большее тремя полюсами (который может содержать полюса underdamped), один нуль, элемент задержки и интегратор.
Вы, должно быть, уже подготовили свои данные, как описано в Подготовка данных.
Можно использовать следующие результаты предполагаемых порядков модели задать порядки модели:
Для первой комбинации ввода/вывода используйте:
Два полюса, соответствуя na=2 в модели ARX.
Задержка 5, соответствуя nk=5 выборкам (или 2,5 минуты) в модели ARX.
Для второй комбинации ввода/вывода используйте:
Один полюс, соответствуя na=1 в модели ARX.
Задержка 10, соответствуя nk=10 выборкам (или 5 минут) в модели ARX.
Поскольку нет никакого отношения между количеством нулей, оцененных моделью ARX дискретного времени и ее дубликатом непрерывного времени, у вас нет оценки для количества нулей. В этом примере можно задать один нуль для первой комбинации ввода/вывода и никакой нуль для комбинации второго выхода.
Используйте idproc команда, чтобы создать две структуры модели, один для каждой комбинации ввода/вывода:
midproc0 = idproc({'P2ZUD','P1D'}, 'TimeUnit', 'minutes');
Массив ячеек {'P2ZUD','P1D'} задает структуру модели для каждой комбинации ввода/вывода:
'P2ZUD' представляет передаточную функцию с двумя полюсами (P2 ), один нуль (Z ), underdamped (комплексно-сопряженные) полюса (U ) и задержка (D ).
'P1D' представляет передаточную функцию с одним полюсом (P1 ) и задержка (D ).
Пример также использует TimeUnit параметр, чтобы задать модуль используемого времени.
Просмотрите две получившихся модели.
midproc0
midproc0 =
Process model with 2 inputs: y = G11(s)u1 + G12(s)u2
From input 1 to output 1:
1+Tz*s
G11(s) = Kp * ---------------------- * exp(-Td*s)
1+2*Zeta*Tw*s+(Tw*s)^2
Kp = NaN
Tw = NaN
Zeta = NaN
Td = NaN
Tz = NaN
From input 2 to output 1:
Kp
G12(s) = ---------- * exp(-Td*s)
1+Tp1*s
Kp = NaN
Tp1 = NaN
Td = NaN
Parameterization:
'P2DUZ' 'P1D'
Number of free coefficients: 8
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Created by direct construction or transformation. Not estimated.
Значения параметров установлены в NaN потому что они еще не оцениваются.
Установите свойство с временной задержкой объекта модели к 2.5 min и 5 min для каждой пары ввода/вывода как исходные предположения. Кроме того, установите верхний предел для задержки, потому что хорошие исходные предположения доступны.
midproc0.Structure(1,1).Td.Value = 2.5; midproc0.Structure(1,2).Td.Value = 5; midproc0.Structure(1,1).Td.Maximum = 3; midproc0.Structure(1,2).Td.Maximum = 7;
При установке ограничений задержки необходимо задать задержки в терминах фактических единиц измерения времени (минуты, в этом случае) а не количество выборок.
procest итеративное средство оценки моделей процессов, что означает, что оно использует итеративный алгоритм нелинейного метода наименьших квадратов, чтобы минимизировать функцию стоимости. Функция стоимости является взвешенной суммой квадратов ошибок.
В зависимости от его аргументов, procest оценивает различные модели полинома черного ящика. Можно использовать procest, например, чтобы оценить параметры для линейной передаточной функции непрерывного времени, пространства состояний или полиномиальных структур модели. Использовать procest, необходимо предоставить структуре модели неизвестные параметры и данные об оценке как входные параметры.
Для этого фрагмента примера вы, должно быть, уже задали структуру модели, как описано в Определении Структуры Модели процесса. Используйте midproc0 как структура модели и Ze1 как данные об оценке:
midproc = procest(Ze1,midproc0); present(midproc)
midproc =
Process model with 2 inputs: y = G11(s)u1 + G12(s)u2
From input "ConsumptionRate" to output "Production":
1+Tz*s
G11(s) = Kp * ---------------------- * exp(-Td*s)
1+2*Zeta*Tw*s+(Tw*s)^2
Kp = -1.1807 +/- 0.29986
Tw = 1.6437 +/- 714.6
Zeta = 16.036 +/- 6958.9
Td = 2.426 +/- 64.276
Tz = -109.19 +/- 63.734
From input "Current" to output "Production":
Kp
G12(s) = ---------- * exp(-Td*s)
1+Tp1*s
Kp = 10.264 +/- 0.048404
Tp1 = 2.049 +/- 0.054901
Td = 4.9175 +/- 0.034374
Parameterization:
'P2DUZ' 'P1D'
Number of free coefficients: 8
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Termination condition: Maximum number of iterations reached..
Number of iterations: 20, Number of function evaluations: 279
Estimated using PROCEST on time domain data "Ze1".
Fit to estimation data: 86.2%
FPE: 6.081, MSE: 5.984
More information in model's "Report" property.
В отличие от моделей полинома дискретного времени, модели непрерывного времени позволяют вам оценить задержки. В этом случае предполагаемые значения задержки отличаются от исходных предположений, которые вы задали 2.5 и 5 , соответственно. Большая неопределенность в ориентировочных стоимостях параметров G_1(s) укажите что динамика от входа 1 к выходу не получены хорошо.
Чтобы узнать больше об оценке моделей, смотрите Модели процессов.
В этом фрагменте примера вы создаете график, который сравнивает фактический выход и выход модели.
compare(Zv1,midproc)

График показывает, что выход модели обоснованно соглашается с измеренным выходом: существует соглашение о 60% между моделью и данными о валидации.
Используйте resid выполнять остаточный анализ.
resid(Zv1,midproc)

Взаимная корреляция между вторым входом и остаточными ошибками является значительной. График автокорреляции показывает значения за пределами области уверенности и показывает, что остаточные значения коррелируются.
Измените алгоритм для итеративной оценки параметра Levenberg-Marquardt.
Opt = procestOptions;
Opt.SearchMethod = 'lm';
midproc1 = procest(Ze1,midproc,Opt);
Тонкая настройка свойств алгоритма или определение начальных предположений параметра и повторное выполнение оценки могут улучшить результаты симуляции. Добавление шумовой модели может улучшить результаты прогноза, но не обязательно результаты симуляции.
Этот фрагмент примера показывает, как оценить модель процесса и включать шумовую модель в оценку. Включая шумовую модель обычно улучшает результаты прогноза модели, но не обязательно результаты симуляции.
Используйте следующие команды, чтобы задать шум ARMA первого порядка:
Opt = procestOptions;
Opt.DisturbanceModel = 'ARMA1';
midproc2 = procest(Ze1,midproc0,Opt);
Можно ввести 'dist' вместо 'DisturbanceModel'. Имена свойства не являются чувствительными к регистру, и только необходимо включать фрагмент имени, которое однозначно определяет свойство.
Сравните получившуюся модель с результатами измерений.
compare(Zv1,midproc2)

График показывает, что выход модели обеспечивает разумное соглашение с выводом данных валидации.
Выполните остаточный анализ.
resid(Zv1,midproc2)

Остаточный график показывает, что значения автокорреляции в доверительных границах. Таким образом добавление шумовой модели производит некоррелированые остаточные значения. Это указывает на более точную модель.
В этом фрагменте примера вы оцениваете несколько различных типов черного ящика, моделей полинома ввода - вывода.
Вы, должно быть, уже подготовили свои данные, как описано в Подготовка данных.
Можно использовать следующие предыдущие результаты предполагаемых порядков модели задать порядки полиномиальной модели:
Для первой комбинации ввода/вывода используйте:
Два полюса, соответствуя na=2 в модели ARX.
Один нуль, соответствуя nb=2 в модели ARX.
Задержка 5, соответствуя nk=5 выборкам (или 2,5 минуты) в модели ARX.
Для второй комбинации ввода/вывода используйте:
Один полюс, соответствуя na=1 в модели ARX.
Никакие нули, соответствуя nb=1 в модели ARX.
Задержка 10, соответствуя nk=10 выборкам (или 5 минут) в модели ARX.
О Моделях ARX. Для single-input/single-output системы (SISO) структура модели ARX:
y (t) представляет выход во время t, u (t) представляет вход во время t, na является количеством полюсов, nb является количеством нулей плюс 1, nk является количеством выборок, прежде чем вход будет влиять на выход системы (названный задержкой или потеря времени модели), и e (t) является бело-шумовым воздействием.
Структура модели ARX не различает полюса для отдельных путей к вводу/выводу: деление уравнения ARX A, который содержит полюса, показывает, что A появляется в знаменателе для обоих входных параметров. Поэтому можно установить na на сумму полюсов для каждой пары ввода/вывода, которая равна 3 в этом случае.
Продукт System Identification Toolbox оценивает параметры и использование данных и модели приказывает, чтобы вы задали.
Оценка Моделей ARX Используя arx. Используйте arx вычислить полиномиальные коэффициенты с помощью быстрого, неитеративного метода arx:
marx = arx(Ze1,'na',3,'nb',[2 1],'nk',[5 10]); present(marx) % Displays model parameters % with uncertainty information
marx =
Discrete-time ARX model: A(z)y(t) = B(z)u(t) + e(t)
A(z) = 1 - 1.027 (+/- 0.02907) z^-1 + 0.1678 (+/- 0.042) z^-2 + 0.01289 (
+/- 0.02583) z^-3
B1(z) = 1.86 (+/- 0.189) z^-5 - 1.608 (+/- 0.1888) z^-6
B2(z) = 1.612 (+/- 0.07392) z^-10
Sample time: 0.5 minutes
Parameterization:
Polynomial orders: na=3 nb=[2 1] nk=[5 10]
Number of free coefficients: 6
Use "polydata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using ARX on time domain data "Ze1".
Fit to estimation data: 90.7% (prediction focus)
FPE: 2.768, MSE: 2.719
More information in model's "Report" property.
MATLAB оценивает полиномы A , B1 , и B2. Неопределенность для каждого из параметров модели вычисляется к 1 стандартному отклонению и появляется в круглых скобках рядом с каждым значением параметров.
В качестве альтернативы можно использовать следующий краткий синтаксис и задать порядки модели как один вектор:
marx = arx(Ze1,[3 2 1 5 10]);
Доступ к Данным модели. Модель вы оценили, marx, дискретное время idpoly объект. Чтобы получить свойства этого объекта модели, можно использовать get функция:
get(marx)
A: [1 -1.0267 0.1678 0.0129]
B: {[0 0 0 0 0 1.8599 -1.6084] [0 0 0 0 0 0 0 0 0 0 1.6118]}
C: 1
D: 1
F: {[1] [1]}
IntegrateNoise: 0
Variable: 'z^-1'
IODelay: [0 0]
Structure: [1x1 pmodel.polynomial]
NoiseVariance: 2.7436
Report: [1x1 idresults.arx]
InputDelay: [2x1 double]
OutputDelay: 0
Ts: 0.5000
TimeUnit: 'minutes'
InputName: {2x1 cell}
InputUnit: {2x1 cell}
InputGroup: [1x1 struct]
OutputName: {'Production'}
OutputUnit: {'mg/min'}
OutputGroup: [1x1 struct]
Notes: [0x1 string]
UserData: []
Name: ''
SamplingGrid: [1x1 struct]
Можно получить доступ к информации, хранившей этими свойствами с помощью записи через точку. Например, можно вычислить дискретные полюса модели путем нахождения корней A полином.
marx_poles = roots(marx.a)
marx_poles =
0.7953
0.2877
-0.0564
В этом случае вы получаете доступ к A полином с помощью marx.a.
Модель marx описывает системную динамику с помощью трех дискретных полюсов.
Можно также использовать pole вычислить полюса модели непосредственно.
Узнать больше. Чтобы узнать больше об оценке полиномиальных моделей, см. Модели Полинома Ввода - вывода.
Для получения дополнительной информации о доступе к данным модели, смотрите Экстракцию Данных.
О Моделях в пространстве состояний. Общая структура модели в пространстве состояний:
y (t) представляет выход во время t, u (t) представляет вход во время t, x (t) является вектором состояния во время t, и e (t) является бело-шумовым воздействием.
Необходимо задать одно целое число как порядок модели (размерность вектора состояния), чтобы оценить модель в пространстве состояний. По умолчанию задержка равняется 1.
Продукт System Identification Toolbox оценивает матрицы пространства состояний A, B, C, D, и K использование порядка модели и данных, которые вы задаете.
Структура модели в пространстве состояний является хорошим выбором для быстрой оценки, потому что это содержит только два параметра: n количество полюсов (размер матрицы A) и nk задержка.
Оценка Моделей в пространстве состояний Используя n4sid. Используйте n4sid команда, чтобы указать диапазон порядков модели и оценить производительность нескольких моделей в пространстве состояний (порядки 2 - 8):
mn4sid = n4sid(Ze1,2:8,'InputDelay',[4 9]);Эта команда использует быстрое, неитеративное (подпространство) метод и открывает следующий график. Вы используете этот график решить, какие состояния предоставляют значительный относительный вклад в поведение ввода/вывода, и какие состояния предоставляют самый маленький вклад.
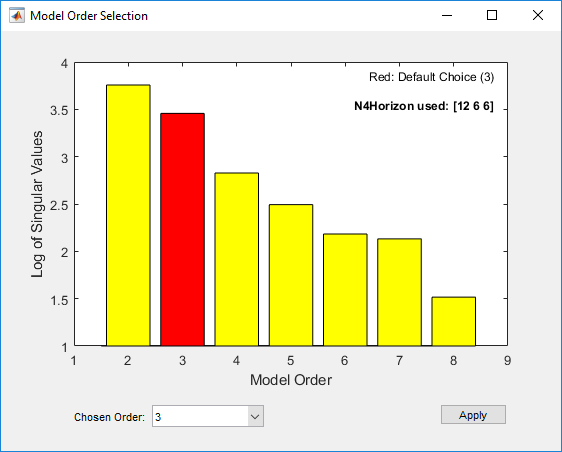
Вертикальная ось является относительной мерой того, сколько каждое состояние вносит в поведение ввода/вывода модели (журнал сингулярных значений ковариационной матрицы). Горизонтальная ось соответствует порядку модели n. Этот график рекомендует n=3, обозначенный красным прямоугольником.
Поле порядка Chosen Order отображает рекомендуемый порядок модели, 3 в этом случае, по умолчанию. Можно изменить выбор порядка при помощи Chosen Order выпадающий список. Примените значение в поле Chosen Order и закройте окно выбора порядка путем нажатия на Apply.
По умолчанию, n4sid использует свободную параметризацию формы пространства состояний. Чтобы оценить каноническую форму вместо этого, установите значение SSParameterization свойство к 'Canonical' . Можно также задать задержку входа к выходу (в выборках) использование 'InputDelay' свойство.
mCanonical = n4sid(Ze1,3,'SSParameterization','canonical','InputDelay',[4 9]); present(mCanonical); % Display model properties
mCanonical =
Discrete-time identified state-space model:
x(t+Ts) = A x(t) + B u(t) + K e(t)
y(t) = C x(t) + D u(t) + e(t)
A =
x1 x2 x3
x1 0 1 0
x2 0 0 1
x3 0.0737 +/- 0.05919 -0.6093 +/- 0.1626 1.446 +/- 0.1287
B =
ConsumptionR Current
x1 1.844 +/- 0.175 0.5633 +/- 0.122
x2 1.063 +/- 0.1673 2.308 +/- 0.1222
x3 0.2779 +/- 0.09615 1.878 +/- 0.1058
C =
x1 x2 x3
Production 1 0 0
D =
ConsumptionR Current
Production 0 0
K =
Production
x1 0.8674 +/- 0.03169
x2 0.6849 +/- 0.04145
x3 0.5105 +/- 0.04352
Input delays (sampling periods): 4 9
Sample time: 0.5 minutes
Parameterization:
CANONICAL form with indices: 3.
Feedthrough: none
Disturbance component: estimate
Number of free coefficients: 12
Use "idssdata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using N4SID on time domain data "Ze1".
Fit to estimation data: 91.39% (prediction focus)
FPE: 2.402, MSE: 2.331
More information in model's "Report" property.
mn4sid и mCanonical модели дискретного времени. Чтобы оценить модель непрерывного времени, установите 'Ts' свойство к 0 в команде оценки или использовании ssest команда:
mCT1 = n4sid(Ze1, 3, 'Ts', 0, 'InputDelay', [2.5 5]) mCT2 = ssest(Ze1, 3,'InputDelay', [2.5 5])
Узнать больше. Чтобы узнать больше об оценке моделей в пространстве состояний, смотрите Модели в пространстве состояний.
О Моделях Поля-Jenkins. Общая структура Поля-Jenkins (BJ):
Чтобы оценить модель BJ, необходимо задать параметры nb, nf, nc, без обозначения даты, и nk.
Принимая во внимание, что структура модели ARX не различает полюса для отдельных путей к вводу/выводу, модель BJ обеспечивает больше гибкости в моделировании полюсов и нулей воздействия отдельно от полюсов и нулей системной динамики.
Оценка Модели BJ Используя pem. Можно использовать pem оценить модель BJ. pem итерационный метод и имеет следующий общий синтаксис:
pem(data,'na',na,'nb',nb,'nc',nc,'nd',nd,'nf',nf,'nk',nk)
Чтобы оценить модель BJ, введите:
na = 0; nb = [ 2 1 ]; nc = 1; nd = 1; nf = [ 2 1 ]; nk = [ 5 10]; mbj = polyest(Ze1,[na nb nc nd nf nk]);
Эта команда задает nf=2 , nb=2 , nk=5 для первого входа и nf=nb=1 и nk=10 для второго входа.
Отобразите информацию модели.
present(mbj)
mbj =
Discrete-time BJ model: y(t) = [B(z)/F(z)]u(t) + [C(z)/D(z)]e(t)
B1(z) = 1.823 (+/- 0.1792) z^-5 - 1.315 (+/- 0.2367) z^-6
B2(z) = 1.791 (+/- 0.06431) z^-10
C(z) = 1 + 0.1068 (+/- 0.04009) z^-1
D(z) = 1 - 0.7452 (+/- 0.02694) z^-1
F1(z) = 1 - 1.321 (+/- 0.06936) z^-1 + 0.5911 (+/- 0.05514) z^-2
F2(z) = 1 - 0.8314 (+/- 0.006441) z^-1
Sample time: 0.5 minutes
Parameterization:
Polynomial orders: nb=[2 1] nc=1 nd=1 nf=[2 1]
nk=[5 10]
Number of free coefficients: 8
Use "polydata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Termination condition: Near (local) minimum, (norm(g) < tol)..
Number of iterations: 6, Number of function evaluations: 13
Estimated using POLYEST on time domain data "Ze1".
Fit to estimation data: 90.75% (prediction focus)
FPE: 2.733, MSE: 2.689
More information in model's "Report" property.
Неопределенность для каждого из параметров модели вычисляется к 1 стандартному отклонению и появляется в круглых скобках рядом с каждым значением параметров.
Полиномы C и D дайте числитель и знаменатель шумовой модели, соответственно.
В качестве альтернативы можно использовать следующий краткий синтаксис, который задает порядки как один вектор:
mbj = bj(Ze1,[2 1 1 1 2 1 5 10]);
bj версия pem это в частности оценивает структуру модели BJ.
Узнать больше. Чтобы узнать больше об идентификации моделей полинома ввода - вывода, таких как BJ, см. Модели Полинома Ввода - вывода.
Сравните выход ARX, пространства состояний и моделей Box-Jenkins к измеренному выходу.
compare(Zv1,marx,mn4sid,mbj)

compare строит измеренный выход в наборе данных валидации против симулированного выхода из моделей. Входные данные от набора данных валидации служат входом к моделям.
Выполните остаточный анализ ARX, пространства состояний и моделей Box-Jenkins.
resid(Zv1,marx,mn4sid,mbj)

Все три модели симулируют выход одинаково хорошо и имеют некоррелированые остаточные значения. Поэтому выберите модель ARX, потому что это является самым простым из трех моделей полинома ввода - вывода и соответственно получает динамику процесса.
В этом фрагменте примера вы симулируете выход модели. Вы, должно быть, уже создали модель midproc2 непрерывного времени, как описано в Оценке Моделей процессов.
Симуляция выхода модели запрашивает следующую информацию:
Входные значения к модели
Начальные условия для симуляции (также названный начальными состояниями)
Например, следующие команды используют iddata и idinput команды, чтобы создать набор входных данных и использовать sim симулировать выход модели:
% Create input for simulation U = iddata([],idinput([200 2]),'Ts',0.5,'TimeUnit','min'); % Simulate the response setting initial conditions equal to zero ysim_1 = sim(midproc2,U);
Чтобы максимизировать подгонку между симулированным ответом модели к измеренному выходу для того же входа, можно вычислить начальные условия, соответствующие результатам измерений. Начальные условия оптимальной подгонки могут быть получены при помощи findstates на версии пространства состояний предполагаемой модели. Следующие команды оценивают начальные состояния X0est от набора данных Zv1:
% State-space version of the model needed for computing initial states
midproc2_ss = idss(midproc2);
X0est = findstates(midproc2_ss,Zv1);
Затем симулируйте модель с помощью начальных состояний, оцененных из данных.
% Simulation input Usim = Zv1(:,[],:); Opt = simOptions('InitialCondition',X0est); ysim_2 = sim(midproc2_ss,Usim,Opt);
Сравните симулированный и измеренный выход на графике.
figure
plot([ysim_2.y, Zv1.y])
legend({'model output','measured'})
xlabel('time'), ylabel('Output')

Много приложений системы управления требуют, чтобы вы предсказали будущие выходные параметры динамической системы с помощью прошлых данных о вводе/выводе.
Например, используйте predict предсказать ответ модели пять шагов вперед:
predict(midproc2,Ze1,5)

Сравните предсказанные выходные значения с измеренными выходными значениями. Третий аргумент compare задает прогноз "пять шагов вперед". Когда вы не задаете третий аргумент, compare принимает бесконечный горизонт прогноза и симулирует выход модели вместо этого.
compare(Ze1,midproc2,5)

Используйте pe вычислить ошибку прогноза Err между предсказанным выходом midproc2 и измеренный выход. Затем постройте ошибочный спектр с помощью spectrum команда.
[Err] = pe(midproc2,Zv1); spectrum(spa(Err,[],logspace(-2,2,200)))

Ошибки прогноза построены с доверительным интервалом с 1 стандартным отклонением. Ошибки больше в высоких частотах из-за высокочастотной природы воздействия.