plot::PlaneПлоскость Бога в 3D
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
plot::Plane([x, y, z], <[nx, ny, nz]>, <a = amin .. amax>,options) plot::Plane(X, <N>, <a = amin .. amax>,options) plot::Plane(XN, <a = amin .. amax>,options) plot::Plane(p1,p2,p3, <a = amin .. amax>,options) plot::Plane(p123, <a = amin .. amax>,options)
plot::Plane(x, n) создает (бесконечную) плоскость с вектором нормали n, проходящий через точку x.
plot::Plane обеспечивает графическую плоскость в 3D, который не требует спецификации, какую часть плоскости видно в изображении. Видимая часть плоскости определяется автоматически ViewingBox из целой 3D сцены.
Вклад плоскости типа plot::Plane к ViewingBox из 3D сцены состоит только из одной точки [x, y, z] (это - p1, если плоскость задана тремя точками p1, p2, p3 на плоскости).
Таким образом две плоскости с теми же нормальными, но различными точками могут быть математически эквивалентными, но могут произвести различные изображения из-за различных полей просмотра. См. Пример 3.
По умолчанию сетка линий отображена на плоскости. Используйте атрибут Mesh = [n1, n2] с положительными целочисленными значениями n1, n2 управлять количеством линий mesh.
| Атрибут | Цель | Значение по умолчанию |
|---|---|---|
AffectViewingBox | влияние объектов на ViewingBox из сцены | TRUE |
Color | основной цвет | RGB::LightBlue |
Filled | заполненные или прозрачные области и поверхности | TRUE |
FillColor | цвет областей и поверхностей | RGB::LightBlue |
Frames | количество систем координат в анимации | 50 |
Legend | делает запись легенды | |
LegendText | короткий объяснительный текст для легенды | |
LegendEntry | добавить этот объект в легенду? | FALSE |
LineColor | цвет линий | RGB::Black.[0.25] |
LinesVisible | видимость линий | TRUE |
Mesh | количество точек выборки | [15 |
Name | имя объекта графика (для браузера и легенды) | |
Normal | вектор нормали кругов и дисков, и т.д. в 3D | [0 |
NormalX | вектор нормали кругов и дисков, и т.д. в 3D, x-компоненте | 0 |
NormalY | вектор нормали кругов и дисков, и т.д. в 3D, y-компоненте | 0 |
NormalZ | вектор нормали кругов и дисков, и т.д. в 3D, z-компоненте | 1 |
ParameterEnd | закончите значение параметра анимации | |
ParameterName | имя параметра анимации | |
ParameterBegin | начальное значение параметра анимации | |
ParameterRange | область значений параметра анимации | |
Position | положения камер, световых сигналов и текстовых объектов | [0 |
PositionX | x-положения камер, световых сигналов и текстовых объектов | 0 |
PositionY | y-положения камер, световых сигналов и текстовых объектов | 0 |
PositionZ | z-положения камер, световых сигналов и текстовых объектов | 0 |
TimeEnd | время окончания анимации | 10.0 |
TimeBegin | время начала анимации | 0.0 |
TimeRange | оперативный промежуток анимации | 0.0 |
Title | объектный заголовок | |
TitleFont | шрифт объектных заголовков | [" sans-serif ", 11 |
TitlePosition | положение объектных заголовков | |
TitleAlignment | выравнивание по горизонтали заголовков w.r.t. их координаты | Center |
TitlePositionX | положение объектных заголовков, x компонент | |
TitlePositionY | положение объектных заголовков, y компонент | |
TitlePositionZ | положение объектных заголовков, z компонент | |
UMesh | количество точек выборки для параметра “u” | 15 |
VMesh | количество точек выборки для параметра “v” | 15 |
Visible | видимость | TRUE |
VisibleAfter | объект, видимый после этой временной стоимости | |
VisibleBefore | объект, видимый до этой временной стоимости | |
VisibleFromTo | объект, видимый в это время, располагается | |
VisibleAfterEnd | объект, видимый после его законченного времени анимации? | TRUE |
VisibleBeforeBegin | объект, видимый перед его временем анимации, запускается? | TRUE |
Мы генерируем две сферы и плоскость:
plot(plot::Sphere(1, [-1, -1, -1], Color = RGB::Red),
plot::Sphere(1, [ 1, 1, 1], Color = RGB::Green),
plot::Plane([0, 0, 0], [0, 0, 1], Color = RGB::Blue)):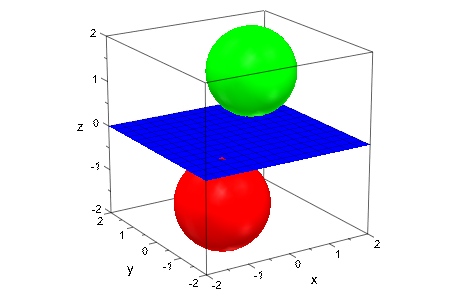
Мы задаем явный ViewingBox для сцены:
plot(plot::Sphere(1, [-1, -1, -1], Color = RGB::Red),
plot::Sphere(1, [ 1, 1, 1], Color = RGB::Green),
plot::Plane([0, 0, 0], [0, 0, 1], Color = RGB::Blue),
ViewingBox = [-3..8, -3..8, -3..3]):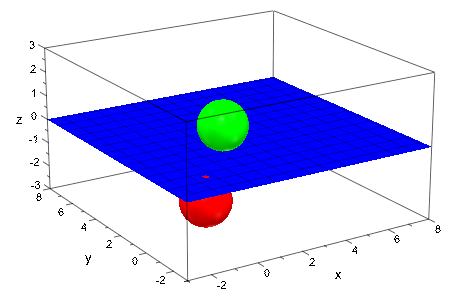
Мы демонстрируем эффект атрибута Mesh это управляет количеством линий mesh, отображенных на плоскостях:
plot(plot::Plane([0, 0, 0], [1, -1, 1], Color = RGB::Red,
Mesh = [5, 5]),
plot::Plane([0, 1, 0], [2, 1, -1], Color = RGB::Green,
Mesh = [10, 10]),
plot::Plane([1, -1, 0], [1, 1, 1], Color = RGB::Blue,
Mesh = [20, 20]),
ViewingBox = [-1..3, -2..2, -2..2])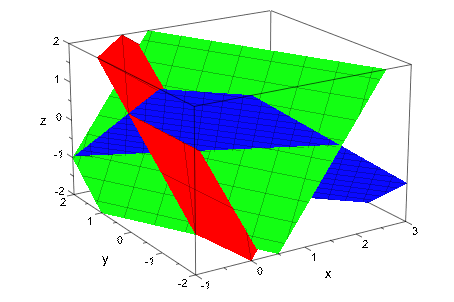
Мы изменяем количество линий mesh:
plot(plot::Plane([0, 0, 0], [1, -1, 1], Color = RGB::Red,
Mesh = [10, 10]),
plot::Plane([0, 1, 0], [2, 1, -1], Color = RGB::Green,
Mesh = [20, 10]),
plot::Plane([1, -1, 0], [1, 1, 1], Color = RGB::Blue,
Mesh = [15, 5]),
ViewingBox = [-1..3, -2..2, -2..2])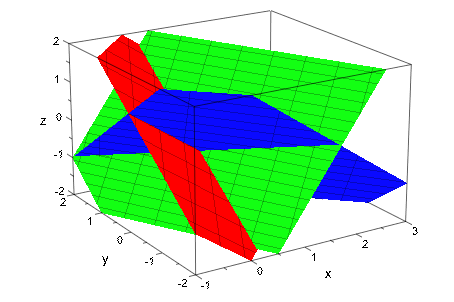
Вклад плоскости к автоматическому ViewingBox из целой сцены состоит только из точки, используемой, чтобы задать плоскость. В следующей сцене эта точка является источником. Это находится в ViewingBox сгенерированный этими двумя сферами. Таким образом, ViewingBox из сцены определяется этими двумя сферами только:
plot(plot::Sphere(1, [1, 1, 1], Color = RGB::Red),
plot::Sphere(1, [-1, -1, -1], Color = RGB::Green),
plot::Plane([0, 0, 0], [0, 0, 1], Color = RGB::Blue)):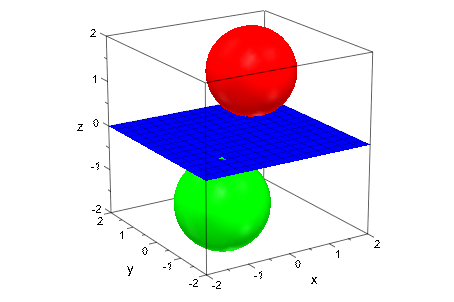
Теперь различная точка [5, 0, 0] используется, чтобы задать ту же плоскость. Это не лежит в ViewingBox сгенерированный этими двумя сферами и таким образом увеличивает ViewingBox из сцены:
plot(plot::Sphere(1, [1, 1, 1], Color = RGB::Red),
plot::Sphere(1, [-1, -1, -1], Color = RGB::Green),
plot::Plane([5, 0, 0], [0, 0, 1], Color = RGB::Blue)):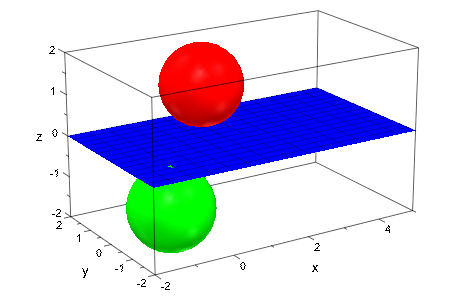
Мы создаем анимированные плоскости:
plot(plot::Plane([0, 0, 0], [cos(a), sin(a), 0], a = 0..PI,
Color = RGB::Red),
plot::Plane([0, 0, 0], [0, cos(a), sin(a)], a = 0..PI,
Color = RGB::Green),
plot::Plane([0, 0, a], [0, 0, 1], a = 0..1,
Color = RGB::Blue),
ViewingBox = [-1..1, -1..1, -1..1])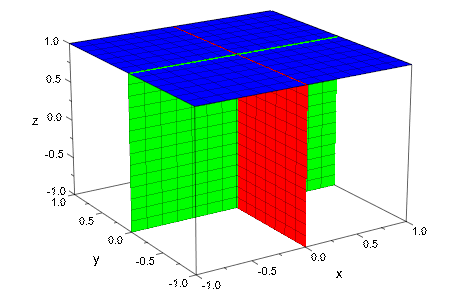
|
Координаты точки на плоскости: числовые действительные значения или арифметические выражения в параметре анимации |
|
Компоненты вектора нормали;
|
|
Матрица A категории
|
|
Матрица A категории
|
|
Матрица A категории |
|
Три точки на плоскости: или списки с 3 записями каждый или матрицы категории |
|
Матрица A категории |
|
Параметр анимации, заданный как |