UMesh, VMesh, USubmesh, VSubmeshКоличество точек выборки
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
UMesh, USubmesh, VMesh, VSubmesh | Наследованный | Положительное целое число |
| Объекты | Значения по умолчанию |
|---|---|
plot::Curve2d, plot::Curve3d, plot::Polar |
|
plot::Cylindrical, plot::SphericalПоверхность графика, plot::XRotate, plot::ZRotate |
|
plot::Rootlocus |
|
plot::Sweep |
|
plot::Plane |
|
plot::Tube |
|
plot::Ode2d, plot::Ode3d |
|
Атрибуты UMesh и т.д. определите количество точек выборки, используемых в числовом приближении параметризованных объектов графика, таких как кривые и поверхности.
Много объектов графика должны быть оценены численно на дискретной mesh. Атрибуты, описанные на этой странице справки, служат для того, чтобы определить номер точек выборки числовой mesh.
Для кривых в 2D и 3D, данном параметризацией x (u), y (u) и, возможно, z (u) параметром кривой u, атрибут UMesh = n создает числовую сетку n равноотстоящие значения u. Атрибут USubmesh = m вставляет дополнительные точки mesh m между каждой парой смежных точек, установленных UMesh.
Комбинации UMesh = n, USubmesh = m и UMesh = (m + 1) (n - 1) + 1, USubmesh = 0 эквивалентны.
Определение Mesh, Submesh оказывает то же влияние как определение UMesh, USubmesh.
Точки выборки кривой могут быть сделаны видимыми установкой PointsVisible = TRUE.
Объекты подложки в 3D параметризованы координатными функциями x (u, v), y (u, v), z (u, v) двух поверхностных параметров u, v.
Атрибут UMesh = nu определяет номер n u точек выборки для первого поверхностного параметра. Атрибут VMesh = nv определяет номер nv точек выборки для второго поверхностного параметра. Параметризация оценена на регулярной сетке n u ×nv значения поверхностных параметров u, v.
С USubmesh, VSubmesh атрибуты, дополнительные равноотстоящие точки выборки могут быть вставлены между каждой парой смежных точек выборки, установленных UMesh, VMesh атрибуты.
С ULinesVisible = TRUE и VLinesVisible = TRUE, соответственно, линии параметра регулярной mesh, установленной атрибутами UMesh, VMesh отображены на поверхности. Точки Additonal вставляются через USubmesh, VSubmesh не создавайте дополнительные линии параметра.
Можно также задать UMesh = nu, VMesh = nv, USubmesh = mu, VSubmesh = mv в более короткой форме Mesh = [nu, nv], Submesh = [mu, mv].
Если адаптивная выборка включена, далее неравноотстоящие точки выборки выбраны автоматически между равноотстоящими точками 'начальной mesh' набор через UMesh, USubmesh, VMesh, VSubmesh атрибуты.
Возможно использовать низкие настройки параметров mesh, чтобы достигнуть специальных эффектов. Как пример, мы чертим параметризацию круга со всего шестью точками оценки:
plot(plot::Curve2d([cos(t), sin(t)], t = 0..2*PI, UMesh = 6,
Scaling = Constrained))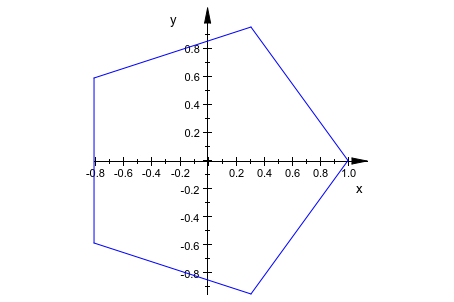
Причина мы получаем пятиугольник здесь и не шестиугольник, состоит в том, что первое и последние точки оценки совпадают: шесть точек в линии означают пять линейных сегментов.
С UMesh = 30, круг похож на круг:
plot(plot::Curve2d([cos(t), sin(t)], t = 0..2*PI, UMesh = 30,
Scaling = Constrained))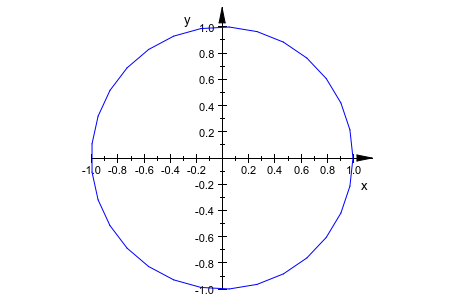
Значения по умолчанию UMesh, VMesh не обеспечивайте достаточное разрешение для следующей графики:
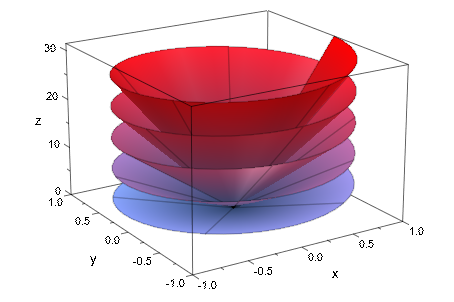
plot(plot::Surface([r*cos(phi), r*sin(phi), r*phi],
r = 0.. 1, phi = 0..10*PI)):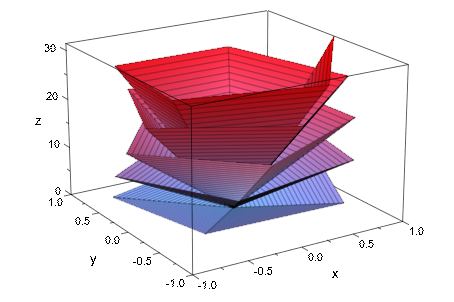
Спираль вьется вокруг z - ось 5 раз. Мы хотим иметь приблизительно 40 точек выборки за оборот, таким образом, мы должны использовать в общей сложности 200 точек выборки относительно углового параметра phi. Координатные линии, связанные с радиальным параметром r прямые линии, таким образом, очень низкое разрешение в этом направлении достаточно:
plot(plot::Surface([r*cos(phi), r*sin(phi), r*phi],
r = 0.. 1, phi = 0..10*PI,
UMesh = 2, VMesh = 200)):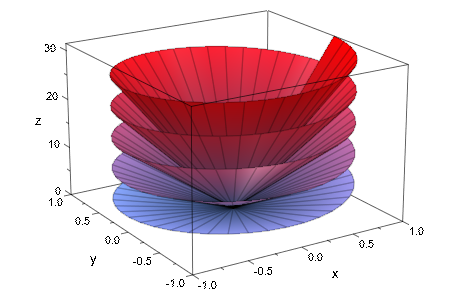
При совершенствовании mesh через VSubmesh, никакие дополнительные линии параметра не создаются:
plot(plot::Surface([r*cos(phi), r*sin(phi), r*phi],
r = 0.. 1, phi = 0..10*PI,
UMesh = 2, VMesh = 25, VSubmesh = 8)):