plot::SequenceПоследовательности
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
plot::Sequence(y,n = n1 .. n2, <a = amin .. amax>,options) plot::Sequence(x,y,n = n1 .. n2, <a = amin .. amax>,options)
plot::Sequence(y(n), n = n_1 .. n_2 ) создает точки
![]() .
.
plot::Sequence(x(n), y(n), n = n_1 .. n_2 ) создает последовательность точек
![]() .
.
plot::Sequence создает графики последовательностей, т.е. функционирует и кривые, заданные по (некоторое подмножество) целые числа.
plot::Sequence(y(n), n = n_1..n_2 ) функционально эквивалентно вызову plot::PointList2d([[n, y(n)] $ n = n_1..n_2 ), и plot::Sequence(x(n), y(n), n = n_1..n_2 ) создает то же изображение как plot::PointList2d([[x(n), y(n)] $ n = n_1..n_2 ). Смотрите Пример 2 для некоторой дополнительной функциональности.
| Атрибут | Цель | Значение по умолчанию |
|---|---|---|
AffectViewingBox | влияние объектов на ViewingBox из сцены | TRUE |
AntiAliased | сглаженные линии и точки? | TRUE |
Color | основной цвет | RGB::Blue |
Frames | количество систем координат в анимации | 50 |
Legend | делает запись легенды | |
LegendText | короткий объяснительный текст для легенды | |
LegendEntry | добавить этот объект в легенду? | FALSE |
LineColor | цвет линий | RGB::Blue |
LineWidth | ширина линий | 0.35 |
LineColor2 | цвет линий | RGB::DeepPink |
LineStyle | тело, подчеркнутые штриховой линией или пунктирные линии? | Solid |
LinesVisible | видимость линий | FALSE |
LineColorType | типы окраски линии | Flat |
LineColorFunction | функциональная окраска линии | |
Name | имя объекта графика (для браузера и легенды) | |
ParameterEnd | закончите значение параметра анимации | |
ParameterName | имя параметра анимации | |
ParameterBegin | начальное значение параметра анимации | |
ParameterRange | область значений параметра анимации | |
PointSize | размер точек | 2 |
PointStyle | стиль презентации точек | FilledCircles |
PointsVisible | видимость точек mesh | TRUE |
TimeEnd | время окончания анимации | 10.0 |
TimeBegin | время начала анимации | 0.0 |
TimeRange | оперативный промежуток анимации | 0.0 |
Title | объектный заголовок | |
TitleFont | шрифт объектных заголовков | [" sans-serif ", 11 |
TitlePosition | положение объектных заголовков | |
TitleAlignment | выравнивание по горизонтали заголовков w.r.t. их координаты | Center |
TitlePositionX | положение объектных заголовков, x компонент | |
TitlePositionY | положение объектных заголовков, y компонент | |
UMax | окончательное значение параметра “u” | |
UMin | начальное значение параметра “u” | |
UName | имя параметра “u” | |
URange | область значений параметра “u” | |
Visible | видимость | TRUE |
VisibleAfter | объект, видимый после этой временной стоимости | |
VisibleBefore | объект, видимый до этой временной стоимости | |
VisibleFromTo | объект, видимый в это время, располагается | |
VisibleAfterEnd | объект, видимый после его законченного времени анимации? | TRUE |
VisibleBeforeBegin | объект, видимый перед его временем анимации, запускается? | TRUE |
XFunction | функция для x значений | |
YFunction | функция для y значений |
Когда дали одно выражение и область значений, plot::Sequence строит последовательность в функциональном стиле:
plot(plot::Sequence((-1)^n/n, n=1..10))
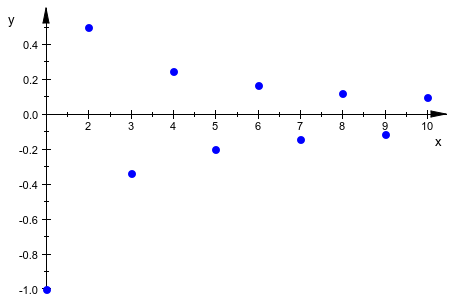
plot::Sequence принимает, что множество атрибутов влияет на внешний вид графика:
plot(plot::Sequence((-1)^n/n, n=1..10,
PointStyle = FilledDiamonds,
PointSize = 4*unit::mm,
Color = RGB::Red),
plot::Sequence(1/n, n=1..10,
PointsVisible = FALSE,
LinesVisible = TRUE),
plot::Sequence(-1/n, n=1..10,
PointsVisible = FALSE,
LinesVisible = TRUE))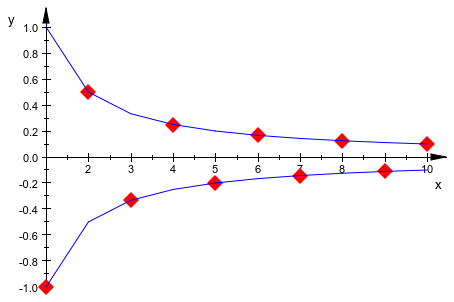
Путем предоставления двух выражений мы можем сделать plot::Sequence постройте последовательность точек, данных двумя выражениями для x - и y - координата:
plot(plot::Sequence(sin(2*PI*n/60), cos(2*PI*n/60),
n = 1..60), Scaling=Constrained)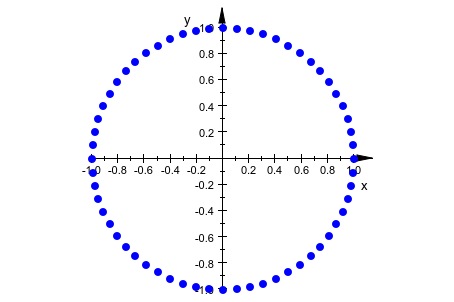
В отличие от plot::PointList2d вызовите упомянутый выше как эквивалентные, plot::Sequence позволяет легко анимировать число точек:
plot(plot::Sequence(sin(2*PI*n/60), cos(2*PI*n/60),
n = 1..nmax, nmax = 1..60),
Scaling=Constrained, Frames = 60, TimeRange = 1..60)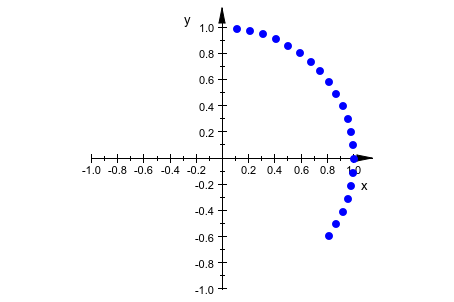
Включением параметра анимации в выражениях x и y, более комплексные анимации возможны. Как пример, мы анимируем итерацию Ньютона для различных начальных значений. В первую очередь, мы задаем шаг итерации, который сопоставляет приближение с его улучшением:
newton := x -> x - f(x)/f'(x):
Для конкретных вычислений мы должны будем использовать определенный функциональный f:
f := x -> sin(2*x) + x^2:
Чтобы получить последовательные шаги итерации, мы будем использовать функциональный оператор итерации @@. Например, третье улучшение начального значения 1.0 вычисляется можно следующим образом:
(newton@@3)(1.0)
![]()
Для нашей анимации мы хотим показать приближения, соответствующие значения функции и порядок, в котором найдены приближения. Кроме того, мы отображаем саму функцию:
function := plot::Function2d(f, x = -2..2):
steps := plot::Sequence((newton@@n)(x0), f((newton@@n)(x0)),
n = 0..5, x0 = -1.25..1.5,
Color = RGB::Green,
LinesVisible = TRUE):
plot(function, steps,
ViewingBox = [-2..2, -1..5], PointSize = 2.5)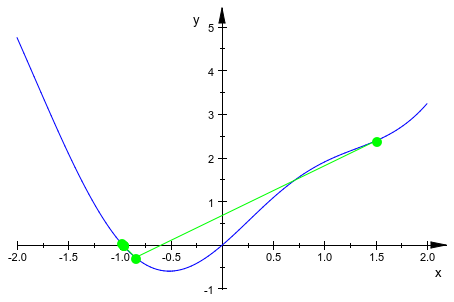
Чтобы далее увеличить число шагов итерации, мы должны снова использовать ранее вычисленные приближения. С этой целью мы используем функцию с option remember:
newtonIter := proc(x0, n)
option remember;
begin
if domtype(n) <> DOM_INT then
return(procname(args()));
end_if;
if iszero(n) then x0
else newton(newtonIter(x0, n-1));
end_if;
end_proc:Кроме того, мы используем plot::Point2d отобразить начальную точку в различном цвете.
steps := plot::Sequence(newtonIter(x0, n), f(newtonIter(x0, n)),
n = 0..10, x0 = -1.25..1.5,
Color = RGB::Green,
LinesVisible = TRUE):
start := plot::Point2d(x0, f(x0), x0 = -1.25..1.5):
plot(function, steps, start,
ViewingBox = [-2..2, -1..5], PointSize = 2.5)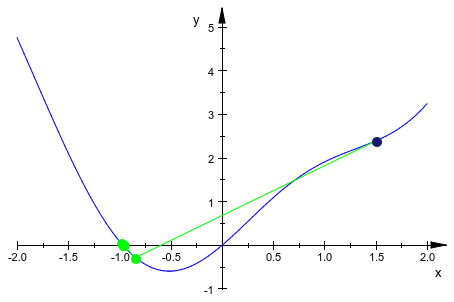
Начиная с f был оценен в наших определениях объектов, мы должны будем переиздать соответствующие команды при изменении f.
|
Арифметические выражения с действительным знаком в |
|
Индекс последовательности: идентификатор или индексируемый идентификатор.
|
|
Область значений индекса |
|
Параметр анимации, заданный как |