Атрибуты

Пример 1

Следующая итерация приводит к так называемому аттрактору Hénon (от теории хаоса):

c1 := 1.4:
c2 := 0.3:
henon_iter := (x, y) -> [c1*x^2+y-1, c2*x]:

Запустите в (0, 0), сотня, которой позволяют, циклов итерации проходит мимо (чтобы только построить аттрактор), и затем собрать следующие три тысячи точек:

[x, y] := [0, 0]:
for i from 1 to 100 do
  [x, y] := henon_iter(x, y);
end_for:
data := {}:
for i from 1 to 3000 do
  [x, y] := henon_iter(x, y);
  data := data union {[x, y]};
end_for:

В этом примере вы собираете данные в наборе, потому что добавление элементов к набору является быстрой операцией, в отличие от изменения длины списка, и вы не должны заботиться о порядке, в котором были достигнуты точки. Чтобы отобразить данные на графике, преобразуйте его в список сначала:

data := coerce(data, DOM_LIST):
plot(plot::PointList2d(data))

Пример 2

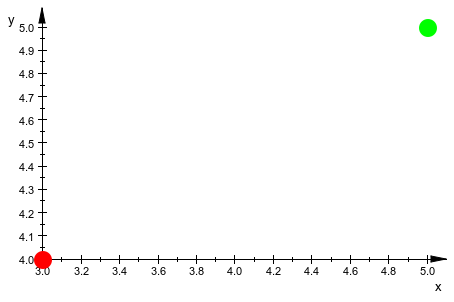
plot::PointList2d позволяет вам задать цвета точек. Например, следующий список содержит две точки. Когда вы строите этот список, первая точка появляется в красном, и вторая точка появляется в зеленом:

Coords := [[3, 4, RGB::Red], [5, 5, RGB::Green]];
plotCoords := plot::PointList2d(Coords):
plot(plotCoords,  PointSize=5)

Если вы задаете цвет одной точки, необходимо также задать цвета всех других точек в списке:

Coords := [[3, 4, RGB::Red], [5, 5]];
plotCoords := plot::PointList2d(Coords)

Error: Attribute 'Points2d' in the 'PointList2d' object must be a list of lists of two expressions and an optional color value. [plot]

Пример 3

(Маршрут удвоения периода Файгенбаума к хаосу)

Считайте итерацию x _{n + 1} = f _p (x _n), где является “логистической картой” параметром p. Карта итерации f _p сопоставляет интервал [0, 1] к себе для 0 ≤ p ≤ 4. Для маленьких значений p последовательность (x _n) имеет конечное число предельных точек, которые посещают циклически. Увеличивая p, разделение предельных точек в 2 отдельных предельных точки для определенных критических значений p (“удвоение периода”). Поскольку, существует бесконечно много предельных точек, и последовательность (x _n) ведет себя хаотично.

Визуализируйте предельные точки как функции p (“схема Feigenbaum”).

Для P близко расположенные значения p создайте последовательность (x _n) начиная с x ₀ = 0.5. Проигнорируйте первые значения N, ожидая что следующий цикл значений M по предельным точкам. Эти точки добавляются к списку plotdata это наконец подано в PointList2d для графического вывода:

f:= (p, x) -> p*x*(1-x):

 P:= 500: // number of steps in p direction
N:= 200: // transitional steps before we are close to the cycle
M:= 300: // maximal number of points on the cycle

 pmin:= 2.8: // Consider p between
pmax:= 4.0: // pmin and pmax
plotdata:= [ ]:
for p in [pmin + i*(pmax - pmin)/P $ i = 0..P] do
    // First, do N iterations to drive the 
    // point x towards the limit cycle 
    x:= 0.5:
    for i from 1 to N do
      x:= f(p, x):
    end_for:

     // consider the next M iterates and use them as plot data:
    xSequence:= table():
    xSequence[1]:= x;
    for i from 2 to M do
        x:= f(p, x):
        if abs(x - xSequence[1]) < 10^(-5) then
           // We are back at the beginning of the cycle;
           // the points will repeat. Go to the next p.
           break;
        else
           xSequence[i]:= x;
        end_if;
    end_for:
    plotdata:= plotdata . [[p, rhs(x)] $ x in xSequence];
end_for:

 plot(plot::PointList2d(plotdata, 
                       PointColor = RGB::Black,
                       PointSize = 0.5*unit::mm)):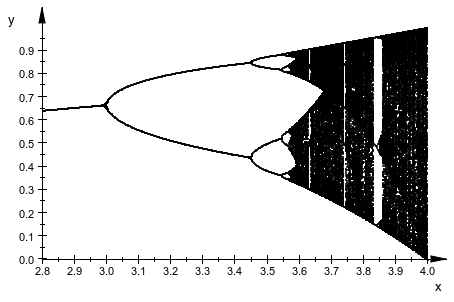

delete f, P, N, M, pmin, pmax, plotdata, x, xSequence, i;

Пример 4

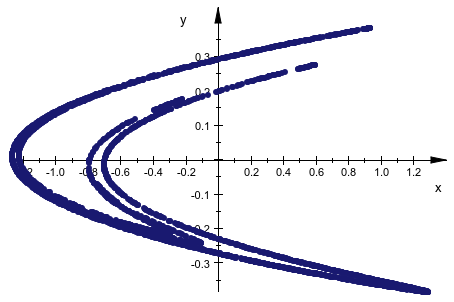
Создайте следующую спираль номера путем графического вывода только простых чисел. Этот график показывает, что кластер начал вдоль конкретных кривых вызвал главно генерирующие кривые.

plot(
     plot::PointList2d([[sqrt(n)*cos(2*PI*sqrt(n)),
                         sqrt(n)*sin(2*PI*sqrt(n))]
                $ n in [ithprime(j) $ j = 1..2345]],
                                      PointSize = 1
     ),
      Axes = None, Scaling = Constrained,
      Height = 100, Width = 100)