`plot`::`SurfaceSet`

Треугольник и четверка появляются сетки

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

plot::SurfaceSet(meshlist, <MeshListType = t>, <MeshListNormals = n>, <UseNormals = b>, <a = a_min .. a_max>, options)

Описание

plot::SurfaceSet(MeshList) создает 3D графический объект из данного списка треугольных или квадратических координат.

MeshList содержит координаты точек (и дополнительные нормали) или треугольников или четверок, которые задают сетку 3D поверхности. Точки должны быть даны однородные: Если нормальное дано, это должно быть дано для всех точек или фасетов, соответственно. Атрибут MeshListType задает, как эти точки должны быть интерпретированы для графического вывода поверхности. Атрибут MeshListNormals задает, содержит ли список векторы нормали и в которых положениях они расположились.

MeshListType задает как точки в MeshList должны быть интерпретированы для графического вывода поверхности. Смотрите MeshList для получения дополнительной информации о mesh перечисляют типы. См. Пример 4.

MeshListNormals задает ли MeshList содержит нормали и в которых положениях они расположены. Смотрите MeshList для получения дополнительной информации о нормалях и фасетной ориентации.

При установке атрибута UseNormals к FALSE нормали заданы в MeshList проигнорированы при графическом выводе объекта в MuPAD^®. Это уменьшает объем данных графического объекта и вычислительное время также. Однако это приводит к менее яркому изображению.

Пользовательские функции управления цветом LineColorFunction и FillColorFunction будет вызван индексом текущей точки как ее первый параметр, сопровождаемый x, y и координатой z текущей точки.

Преобразование возражает plot::Rotate3d, plot::Scale3d, plot::Translate3d и plot::Transform3d может быть применен к импортированному объекту STL. См. Пример 8.

Атрибуты

Атрибут	Цель	Значение по умолчанию
`AffectViewingBox`	влияние объектов на `ViewingBox` из сцены	`TRUE`
`Color`	основной цвет	`RGB::Red`
`Filled`	заполненные или прозрачные области и поверхности	`TRUE`
`FillColor`	цвет областей и поверхностей	`RGB::Red`
`FillColor2`	второй цвет областей и поверхностей для цветных смешений	`RGB::CornflowerBlue`
`FillColorType`	типы заполнения поверхности	`Dichromatic`
`FillColorFunction`	функциональная область / поверхностная окраска
`FillColorDirection`	направление цветовых переходов на поверхностях	[0, 0, 1]
`FillColorDirectionX`	x-компонент направления цветовых переходов на поверхностях	0
`FillColorDirectionY`	y-компонент направления цветовых переходов на поверхностях	0
`FillColorDirectionZ`	z-компонент направления цветовых переходов на поверхностях	1
`Frames`	количество систем координат в анимации	50
`Legend`	делает запись легенды
`LegendText`	короткий объяснительный текст для легенды
`LegendEntry`	добавить этот объект в легенду?	`FALSE`
`LineColor`	цвет линий	`RGB::Black.[0.25]`
`LineWidth`	ширина линий	0.35
`LineColor2`	цвет линий	`RGB::DeepPink`
`LineStyle`	тело, подчеркнутые штриховой линией или пунктирные линии?	`Solid`
`LineColorType`	типы окраски линии	`Flat`
`LineColorFunction`	функциональная окраска линии
`LineColorDirection`	направление цветовых переходов на линиях	[0, 0, 1]
`LineColorDirectionX`	x-компонент направления цветовых переходов на линиях	0
`LineColorDirectionY`	y-компонент направления цветовых переходов на линиях	0
`LineColorDirectionZ`	z-компонент направления цветовых переходов на линиях	1
`MeshList`	данные о триангуляции
`MeshVisible`	видимость неправильных линий mesh в 3D	`FALSE`
`MeshListType`	данные о триангуляции	`Triangles`
`MeshListNormals`	данные о триангуляции	`None`
`Name`	имя объекта графика (для браузера и легенды)
`ParameterEnd`	закончите значение параметра анимации
`ParameterName`	имя параметра анимации
`ParameterBegin`	начальное значение параметра анимации
`ParameterRange`	область значений параметра анимации
`PointSize`	размер точек	1.5
`PointStyle`	стиль презентации точек	`FilledCircles`
`PointsVisible`	видимость точек mesh	`FALSE`
`Shading`	сглаживайте цветное смешение поверхностей	`Smooth`
`TimeEnd`	время окончания анимации	10.0
`TimeBegin`	время начала анимации	0.0
`TimeRange`	оперативный промежуток анимации	0.0.. 10.0
`Title`	объектный заголовок
`TitleFont`	шрифт объектных заголовков	[`" sans-serif "`, 11]
`TitlePosition`	положение объектных заголовков
`TitleAlignment`	выравнивание по горизонтали заголовков w.r.t. их координаты	`Center`
`TitlePositionX`	положение объектных заголовков, x компонент
`TitlePositionY`	положение объектных заголовков, y компонент
`TitlePositionZ`	положение объектных заголовков, z компонент
`UseNormals`	использовать предопределенные нормали?	`TRUE`
`Visible`	видимость	`TRUE`
`VisibleAfter`	объект, видимый после этой временной стоимости
`VisibleBefore`	объект, видимый до этой временной стоимости
`VisibleFromTo`	объект, видимый в это время, располагается
`VisibleAfterEnd`	объект, видимый после его законченного времени анимации?	`TRUE`
`VisibleBeforeBegin`	объект, видимый перед его временем анимации, запускается?	`TRUE`

Примеры

Пример 1

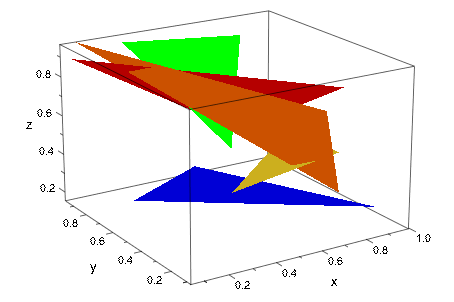
Когда дали список вещественных чисел, plot::SurfaceSet по умолчанию рассматривает их как координаты точек в 3D треугольниках формирования. Обратите внимание на то, что мы используем FillColorFunction здесь, чтобы сделать треугольники легче видеть и что количество значений должно быть делимым 9, поскольку для каждого треугольника нужны 9 чисел, которые будут заданы:

plot(plot::SurfaceSet([frandom() $ i = 1..9*5],
  FillColorFunction = (i -> RGB::ColorList[floor((i+2)/3)]))):

Пример 2

Этот пример демонстрирует, как поверхностные наборы могут быть созданы и анимированы в MuPAD. Сначала мы создаем сетку точек:

delete cx, cy, cz, r:
F:= [[[cx-r  ,cy-r+a,cz+r], [cx-r+a,cy-r  ,cz+r], 
      [cx+r-a,cy-r  ,cz+r], [cx+r  ,cy-r+a,cz+r],
      [cx+r  ,cy+r-a,cz+r], [cx+r-a,cy+r  ,cz+r],
      [cx-r+a,cy+r  ,cz+r], [cx-r  ,cy+r-a,cz+r]],
     [[cx+r,cy-r  ,cz-r+a], [cx+r,cy-r+a,cz-r  ],  
      [cx+r,cy+r-a,cz-r  ], [cx+r,cy+r  ,cz-r+a],
      [cx+r,cy+r  ,cz+r-a], [cx+r,cy+r-a,cz+r  ],
      [cx+r,cy-r+a,cz+r  ], [cx+r,cy-r  ,cz+r-a]],
     [[cx-r  ,cy+r,cz-r+a], [cx-r+a,cy+r,cz-r  ],
      [cx+r-a,cy+r,cz-r  ], [cx+r  ,cy+r,cz-r+a],
      [cx+r  ,cy+r,cz+r-a], [cx+r-a,cy+r,cz+r  ],
      [cx-r+a,cy+r,cz+r  ], [cx-r  ,cy+r,cz+r-a]]]:

F:= F.[subs(F[1], cz+r=cz-r), 
       subs(F[2], cx+r=cx-r), 
       subs(F[3], cy+r=cy-r)]:

T:= [[cx+r,cy-r+a,cz+r], [cx+r-a,cy-r,cz+r], [cx+r,cy-r,cz+r-a]]:
T:= T.subs(T, cx+r-a=cx-r+a, cx+r=cx-r):
T:= T.subs(T, cy-r+a=cy+r-a, cy-r=cy+r):
T:= T.subs(T, cz+r-a=cz-r+a, cz+r=cz-r):

Затем мы создаем объекты графика с помощью mesh выше:

cx := 0: cy := 0: cz := 0:
r := 1: 
P := range -> 
  plot::Group3d(
    plot::Group3d(
        plot::SurfaceSet(map(F[i], op), a = range,
                         MeshListType = TriangleFan) 
        $ i=1..6),
    plot::Group3d(
        plot::Polygon3d(F[i], a = range, Closed) $ i=1..6,
        LineWidth = 1.5,
        LineColor = RGB::Grey,
        PointsVisible,
        PointSize = 3),
      plot::Group3d(
        plot::SurfaceSet(map(T, op), a = range), 
        FillColorType = Flat,
        FillColor=RGB::Yellow,
        Filled)
  ):

plot(P(0..r),
     Scaling = Constrained,
     Width = 120, Height = 120,
     Axes = None):

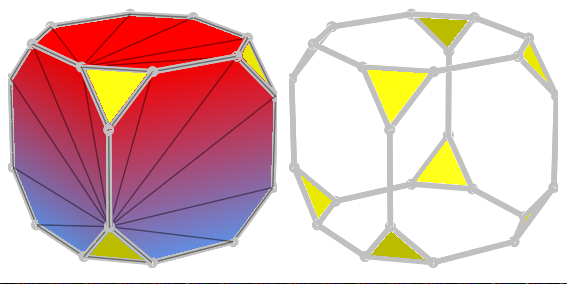
Первая половина этой анимации построена снова. В левом изображении мы видим, как части поверхностного набора создаются как треугольный вентилятор. В правильных частях изображений поверхности отображены как каркас:

plot(
  plot::Scene3d(P(0..r/2), MeshVisible = TRUE),
  plot::Scene3d(P(0..r/2), Filled = FALSE),
  Scaling = Constrained, Width = 150, Height = 75, 
  Axes = None, Layout = Horizontal
):

Пример 3

Вторая анимация демонстрирует сгиб назад куба:

r := 1:
bottom := [[0, 0, 0], [r, 0, 0],
           [r, r, 0], [0, r, 0]]:
left   := [[0, 0, 0], [0, -r*sin(a), r*cos(a)],
           [r, -r*sin(a), r*cos(a)], [r, 0, 0]]:
right  := map(left, l -> [l[1], r-l[2], l[3]]):
front  := map(left, l -> [l[2], l[1], l[3]]):
back   := map(right, l -> [l[2], l[1], l[3]]):
top    := [left[3], left[2],
           zip(left[2], [0, -r*sin(2*a-PI/2), r*cos(2*a-PI/2)], `+`),
           zip(left[3], [0, -r*sin(2*a-PI/2), r*cos(2*a-PI/2)], `+`)]:

plot(plot::SurfaceSet(map(bottom.left.top.right.front.back, op),
                      MeshListType = Quads,
                      PointsVisible = TRUE,
                      PointSize = 3,
                      MeshVisible = TRUE,
                      LineWidth = 1.5,
                      LineColor = RGB::Grey,
                      a=0..PI/2),
     plot::MuPADCube(Radius = r/3, Center = [r/2 $ 3]),
     Scaling = Constrained)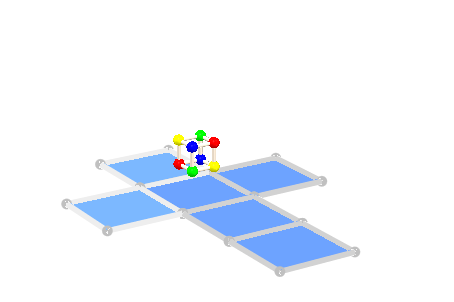

delete r, bottom, left, right, front, back, top:

Пример 4

Давайте иметь более глубокий взгляд на другой вид типов mesh. Мы создаем сетку точек сначала и затем строим ее с помощью различных доступных типов mesh. Первая точка будет всегда строиться в красном цвете:

PL:= [((0,i,0.5-0.1*i), (1,i,0.5-0.1*i)) $ i = 0..5]:
SO:= FillColorFunction = 
     ((n,x,y,z)->[RGB::Blue,RGB::Red,RGB::Green][(n mod 3)+1]), 
     LineColorFunction = 
     ((n,x,y,z)-> if n=1 then RGB::Red else RGB::Black end_if), 
     PointsVisible:
VO:= plot::Camera([0.5,2.5,4.5], [0.5,2.51,0], 0.2),
     ViewingBox = [0..1,0..5,0..0.5], 
     Axes = None:

Мы говорим MuPAD интерпретировать данный список mesh как набор отдельных треугольников. Соответствующий график выглядит так:

plot(plot::SurfaceSet(PL, SO, MeshListType = Triangles), VO):

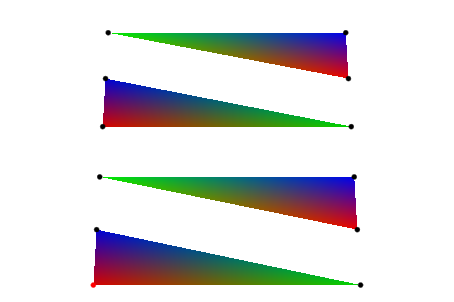
Мы говорим MuPAD интерпретировать данный список mesh как треугольному вентилятору. Соответствующий график выглядит так:

plot(plot::SurfaceSet(PL, SO, MeshListType = TriangleFan), VO):

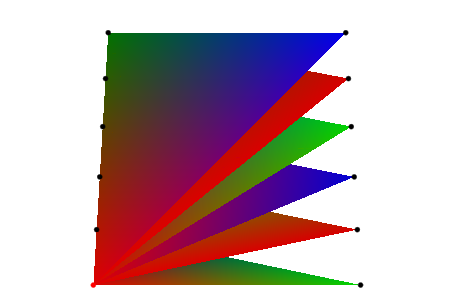
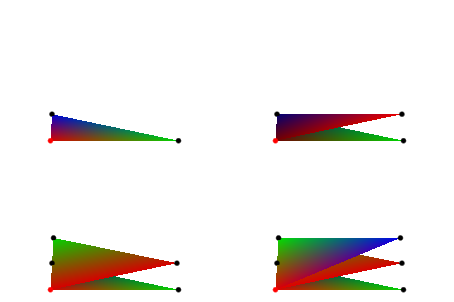
График выше выглядит немного сбивающим с толку, таким образом мы позволяем MuPAD построить первые четыре треугольника шаг за шагом для того, чтобы изучить, как целый вентилятор будет создан:

plot( 
  plot::Scene3d(
    plot::SurfaceSet(PL[1..3*n], SO, MeshListType = TriangleFan), 
    VO
  ) $ n=3..6
):

Мы говорим MuPAD интерпретировать данный список mesh как треугольную полосу. Соответствующий график выглядит так:

plot(plot::SurfaceSet(PL, SO, MeshListType = TriangleStrip), VO):

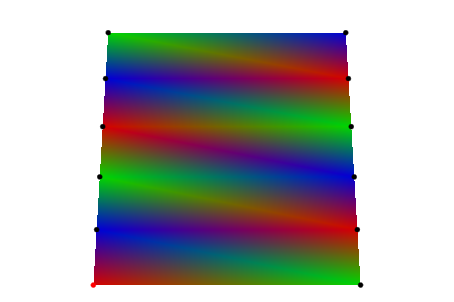
Мы говорим MuPAD интерпретировать данный список mesh как набор отдельных четверок. Соответствующий график выглядит так:

plot(plot::SurfaceSet(PL, SO, MeshListType = Quads), VO):

Причиной того, чтобы построить треугольники вместо (ожидаемый) прямоугольники является порядок точек в списке точек. Изменяя порядок второй и третьей точки, мы получаем ожидаемый результат:

PK:= PL: tmp:= PK[7]: PK[7]:= PK[10]: PK[10]:=tmp:
plot(plot::SurfaceSet(PK, SO, MeshListType = Quads), VO):
delete PK, tmp:

Мы говорим MuPAD интерпретировать данный список mesh как квадратическую полосу. Соответствующий график выглядит так:

plot(plot::SurfaceSet(PL, SO, MeshListType = QuadStrip), VO):
delete PL, SO, VO:

Пример 5

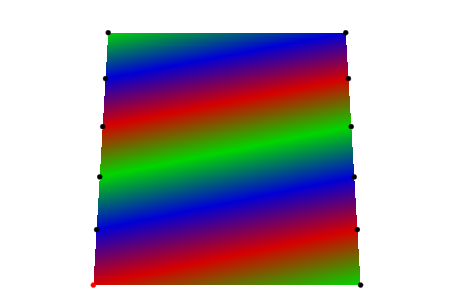
Возможно включать нормали, чтобы дать сглаженную штриховку для поверхностей, которые, как предполагается, не похожи на плоские треугольники. В следующем примере мы используем триангуляцию прямоугольника:

trias := [([x,  y   ], [(x+1), y], [ x   ,(y+1)],
           [x, (y+1)], [(x+1), y], [(x+1),(y+1)])
         $ x = 1..4 $ y = 1..4]:

Сопоставляя функцию с этими точками, мы получаем следующую объемную поверхностную диаграмму:

f := (x,y) -> sin(x)*cos(y):
meshList := map(trias, l -> [l[1], l[2], f(l[1], l[2])]):
plot(plot::SurfaceSet(meshList, MeshListType = Triangles))

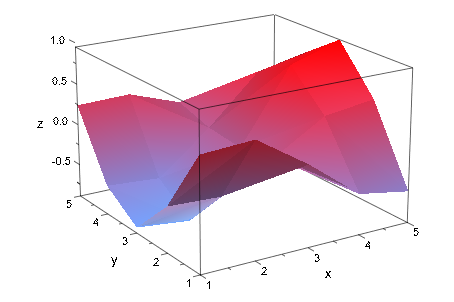
Триангуляция ясно отображается. Один способ уменьшать это состоял бы в том, чтобы совершенствовать mesh, но это может занять много времени с более сложными функциями или быть абсолютно невозможно для данных об измерении. Это намного быстрее, чтобы дать MuPAD больше информации о поверхности, а именно, направлении плоскостей касательной в точках, которые мы оценили:

normals  := map(trias, l -> [D([1], f)(l[1], l[2]),
                             D([2], f)(l[1], l[2]), 1]):
plot(plot::SurfaceSet(zip(meshList, normals, _exprseq),
                      MeshListType = Triangles,
                      MeshListNormals = BehindPoints))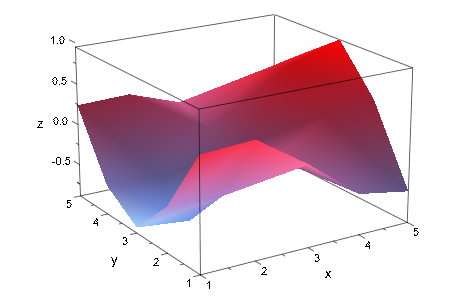

Как вы видите (особенно на границе; в противном случае включите LinesVisible), MuPAD все еще чертит треугольники в точно тех же местах, но использует штриховку цвета, чтобы создать иллюзию сглаженной поверхности.

Пример 6

Мы создаем треугольную mesh с нормалями перед каждым треугольником и строим этот объект, четырехгранник, впоследствии:

meshList:= [
   0.0 ,  0.0 , -1.0 ,
  -1.5 , -1.5 ,  1.4 ,  0.0,  1.7, 1.4, 1.5, -1.5,  1.4,
   0.0 ,  0.88,  0.47,
  -1.5 , -1.5 ,  1.4 ,  1.5, -1.5, 1.4, 0.0,  0.0, -1.4,
  -0.88, -0.41,  0.25,
   1.5 , -1.5 ,  1.4 ,  0.0,  1.7, 1.4, 0.0,  0.0, -1.4,
   0.88, -0.41,  0.25,
   0.0 ,  1.7 ,  1.4 , -1.5, -1.5, 1.4, 0.0,  0.0, -1.4
]:
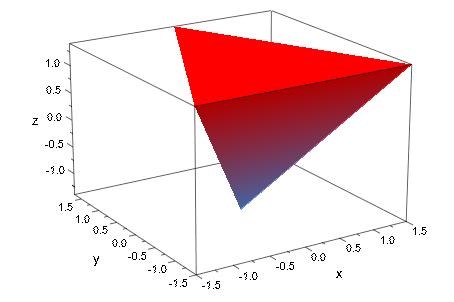
plot(
  plot::SurfaceSet(meshList,
        MeshListType    = Triangles,
        MeshListNormals = BeforeFacets
  )
):

Пример 7

Функция управления цветом FillColorFunction может быть задан. Процедура называется для каждой вершины: параметры являются индексом текущего треугольника, сопровождаемого x-, y-и z-координатой текущей вершины:

plot(
  plot::Scene3d(
    plot::SurfaceSet(meshList, MeshListNormals = BeforeFacets,
      MeshVisible = TRUE,
      LineColor    = RGB::Black,
      FillColorFunction =
      (n ->[RGB::Red,RGB::Blue,RGB::Green,RGB::Yellow]
             [n+2 div 3])
    )
  ),
  plot::Scene3d(
    plot::SurfaceSet(meshList, MeshListNormals = BeforeFacets,
      MeshVisible = TRUE,
      LineColor    = RGB::Black,
      FillColorFunction = ((n,x,y,z) -> [x/2,y/2,z/2])
    )
  ),
  Axes = None, Layout = Horizontal
):

То же самое верно для LineColorFunction:

plot(
  plot::Scene3d(
    plot::SurfaceSet(meshList, MeshListNormals = BeforeFacets,
      MeshVisible  = TRUE,
      PointsVisible = TRUE,
      Filled        = FALSE,
      LineWidth     = 2,
      LineColorFunction =
      (n -> [RGB::Red,RGB::Blue,RGB::Green,RGB::Yellow][n+2 div 3])
    )
  ),
  plot::Scene3d(
    plot::SurfaceSet(meshList, MeshListNormals = BeforeFacets,
      MeshVisible  = TRUE,
      PointsVisible = TRUE,
      Filled        = FALSE,
      LineWidth     = 2,
      LineColorFunction = ((n,x,y,z) -> [x/4,y/4,z/4])
    )
  ),
  Axes = None, Layout = Horizontal
):

Пример 8

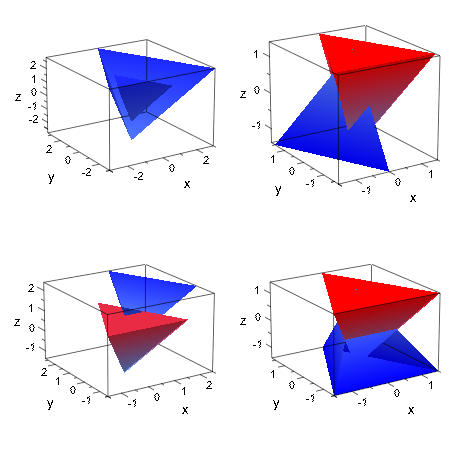
Снова мы строим объект, заданный в Примере 6, но теперь мы добавляем вращаемую, масштабированную и переведенную копию его:

plot(
  plot::Scene3d(
    plot::SurfaceSet(meshList, MeshListNormals = BeforeFacets),
    plot::Scale3d([2,2,2],
      plot::SurfaceSet(meshList, MeshListNormals = BeforeFacets,
                       Color = RGB::Blue.[0.1])
    )
  ),
  plot::Scene3d(
    plot::SurfaceSet(meshList, MeshListNormals = BeforeFacets),
    plot::Rotate3d(PI, Axis=[1,0,0],
      plot::SurfaceSet(meshList, MeshListNormals = BeforeFacets,
                        Color = RGB::Blue.[0.1])
    )
  ),
  plot::Scene3d(
    plot::SurfaceSet(meshList, MeshListNormals = BeforeFacets),
    plot::Translate3d([1,1,1],
      plot::SurfaceSet(meshList, MeshListNormals = BeforeFacets,
                        Color = RGB::Blue.[0.1])
    )
  ),
  plot::Scene3d(
    plot::SurfaceSet(meshList, MeshListNormals = BeforeFacets),
    plot::Transform3d([0,0,0], [1,0,0, 0,1,0, 0,0,-1],
      plot::SurfaceSet(meshList, MeshListNormals = BeforeFacets,
                        Color = RGB::Blue.[0.1])
    )
  ),
  Width = 120, Height = 120
):

Параметры

meshlist

Список точек: список координат типа DOM_FLOAT.

meshlist эквивалентно атрибуту MeshList.

a

Параметр анимации, заданный как a _{= amin..amax}, где _amin начальное значение параметров и _amax итоговое значение параметров.

Опции

MeshListType

Опция, заданная как MeshListType = t

t может быть Triangles, TriangleFan, TriangleStrip, Quads или QuadStrip. Этот атрибут задает вид поверхностной mesh, данной в MeshList. Это означает, что задает, как точка координирует в MeshList должны быть интерпретированы.

MeshListNormals

Опция, заданная как MeshListNormals = n

n может быть None, BeforePoints, BehindPoints, BeforeFacets или BehindFacets. Этот атрибут задает ли MeshList содержит векторы нормали и в которых положениях они расположены.

UseNormals

Опция, заданная как UseNormals = b

b может быть TRUE или FALSE. Этот атрибут задает, используются ли нормали, заданные в файле STL, в графике MuPAD.

Алгоритмы

Нормальный из фасета (треугольник или четверка) данный в MeshList используется во всех его вершинах при графическом выводе этого объекта. Вследствие того, что некоторые фасеты могут совместно использовать точки с другими фасетами, эти точки могут быть заданы с различными нормалями.

Смотрите также

Функции MuPAD

plot | readbytes

MuPAD графические примитивы

plot::Rotate3d | plot::Scale3d | plot::Surface | plot::SurfaceSTL | plot::Transform3d | plot::Translate3d

Документация