factorВключите полином в неприводимые полиномы
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
factor(f, <Adjoin = adjoin>, <MaxDegree = n>) factor(f,F | Domain = F | Full)
factor(f) вычисляет факторизацию f = u f1e1 … f r e r полиномиального f, где u является содержимым f, f 1, …, f r отличные примитивные неприводимые факторы f и e 1, …, e, r является положительными целыми числами.
factor переписывает его аргумент как продукт как можно большего количества условий. В некотором смысле это - дополнительная функция expand, который переписывает его аргумент как сумму как можно большего количества условий.
Если f полином, содействующим звонком которого не является Expr, затем f учтен по его содействующему звонку. Смотрите Пример 10.
Если f полином с содействующим звонком Expr, затем f учтен по самому маленькому звонку, содержащему коэффициенты. Математически, этот подразумеваемый содействующий звонок всегда содержит кольцевой ℤ целых чисел. Смотрите Пример 4. Если коэффициент звонит R 'off' не Expr, затем мы говорим, что подразумеваемым содействующим звонком является R. Элементы подразумеваемого содействующего звонка считаются константами и не учтены дальше. В частности, содержимое u является элементом подразумеваемого содействующего звонка.
С опцией Adjoin, элементы adjoin также примкнуты к содействующему звонку.
Если второй аргумент F или, альтернативно, Domain = F дан, затем f учтен по вещественным числам ℝ или комплексные числа ℂ. Факторизация по ℝ или ℂ выполняется с помощью числовых вычислений, и результаты будут содержать числа с плавающей запятой. Смотрите Пример 5.
Если f арифметическое выражение, но не номер, это рассматривается как рациональное выражение. Нерациональные подвыражения, такие как sin(x), exp(1), x^(1/3) и т.д., но не постоянные алгебраические подвыражения, такие как I и (sqrt(2)+1)^3, заменяются вспомогательными переменными перед факторингом. Алгебраические зависимости подвыражений, таких как уравнение cos (x) 2 = 1 - sin (x) 2, не обязательно учтены. Смотрите Пример 7.
Получившееся выражение затем записано как частное двух многочленных выражений в оригинале и вспомогательном indeterminates. Числитель и знаменатель преобразованы в полиномы с содействующим звонком Expr через poly, и подразумеваемый содействующий звонок является самым маленьким звонком, содержащим коэффициенты полинома числителя и полинома знаменателя. Обычно, это - звонок целых чисел. Затем оба полинома учтены по подразумеваемому содействующему звонку и кратности e, i, соответствующий факторам знаменателя, является отрицательными целыми числами; смотрите Пример 3. После факторизации вспомогательные переменные заменяются исходными подвыражениями. Смотрите Пример 6.
Если f целое число, затем оно разложено на продукт начал, и результат эквивалентен для ifactor. Если f рациональное число, затем и числитель и знаменатель разложены на продукт начал. В этом случае кратность e i, соответствующий факторам знаменателя, является отрицательными целыми числами. Смотрите Пример 2.
Если f число с плавающей точкой или комплексное число, затем factor возвращает факторизацию с одним факторным f.
Результат factor объект доменного типа Factored. Позвольте g:=factor(f) будьте таким объектом.
Это представлено внутренне list[u, f1, e1, ..., fr, er] из нечетной длины 2 r + 1. Здесь, f1 через fr имеют тот же тип как вход (или полиномы или выражения); e1 через er целые числа; и u арифметическое выражение.
Можно извлечь содержимое u и условия f i e i оператором показателя преломления обыкновенной волны [ ], т.е. g[1] = f1^e1, g[2] = e1^e2, ... если u = 1 и g[1] = u, g[2] = f1^e1, g[3] = e1^e2, ..., соответственно, если u ≠ 1.
Вызов Factored::factors(g) дает к списку [f1, f2, ...] из факторов, вызов Factored::exponents(g) возвращает список [e1, e2, ...] из экспонент.
Вызов coerce(g,DOM_LIST) возвращает внутреннее представление учтенного объекта, т.е. список [u, f1, e1, f2, e2, ...].
Обратите внимание на то, что результат factor распечатан как выражение, и оно неявно преобразовано в выражение каждый раз, когда оно обрабатывается далее другими функциями MuPAD®. Как пример, результат q:=factor(x^2+2*x+1) распечатан как (x+1)^2, который является выражением типа "_power".
Смотрите Пример 1 для рисунков и страницы справки Factored для деталей.
Если f не номер, затем каждый из полиномов p 1, …, p r примитивен, т.е. наибольший общий делитель его коэффициентов (см. content и gcd) по подразумеваемому содействующему звонку (см. выше для определения) тот.
В настоящее время факторинг полиномов возможен по следующим подразумеваемым содействующим звонкам: целые числа, вещественные числа, комплексные числа и рациональные числа, конечные поля — представленный IntMod(n) или Dom::IntegerMod(n) для простого числа n, или Dom::GaloisField—, и звонки получили из этих основных звонков путем взятия полиномиальных звонков (см. Dom::DistributedPolynomial, Dom::MultivariatePolynomial, Dom::Polynomial, и Dom::UnivariatePolynomial), поля частей (см. Dom::Fraction), и алгебраические расширения (см. Dom::AlgebraicExtension).
Если вход f арифметическое выражение, которое не является номером, все происходящие числа с плавающей запятой заменяются приближениями непрерывной дроби. Результат чувствителен к переменной окружения DIGITS, смотрите numeric::rationalize для деталей.
Учитывать полиномиальный x 3 + x, введите:
g := factor(x^3+x)
![]()
Обычно, выражения учтены по звонку целых чисел и факторам с неинтегральными коэффициентами, такими как x - I в примере выше, не рассматриваются.
Можно получить доступ к внутреннему представлению этой факторизации с оператором показателя преломления обыкновенной волны:
g[1], g[2]
![]()
Внутреннее представление g, аналогичный описанному выше, дан следующей командой:
coerce(g, DOM_LIST)
![]()
Результатом факторизации является объект доменного типа Factored:
domtype(g)
![]()
Часть функциональности этой области описана в дальнейшем.
Можно извлечь факторы и экспоненты факторизации также следующим образом:
Factored::factors(g), Factored::exponents(g)
![]()
Можно попросить тип факторизации:
Factored::getType(g)
![]()
Этот выход означает, что весь i f неприводим. Другими возможными типами является "squarefree" (см. polylib::sqrfree) или "unknown".
Можно умножить учтенные объекты, который сохраняет учтенную форму:
g2 := factor(x^2 + 2*x + 1)
![]()
g * g2
![]()
Важно отметить, что можно применить (почти) любую функцию, работающую с арифметическими выражениями к объекту типа Factored. Однако результат затем обычно не имеет доменного типа Factored:
expand(g); domtype(%)
![]()
![]()
Для подробного описания этих объектов обратитесь к странице справки доменного Factored.
factor разделяет целое число в продукт простых множителей:
factor(8)
![]()
Для рациональных чисел учтены и числитель и знаменатель:
factor(10/33)
![]()
Обратите внимание на то, что, напротив, постоянные полиномы не учтены:
factor(poly(8, [x]))
![]()
Факторы знаменателя обозначаются отрицательной кратностью:
factor((z^2 - 1)/z^2)
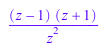
Factored::factors(%), Factored::exponents(%)
![]()
Если некоторые коэффициенты являются иррациональными, но алгебраическими, факторизация происходит по самому маленькому полевому расширению rationals, который содержит всех их. Следовательно, x^2+1 рассматривается неприводимым в то время как его I- сгиб рассматривается приводимым:
factor(x^2 + 1), factor(I*x^2 + I)
![]()
MuPAD автоматически не учитывает по полю алгебраических чисел; только к коэффициентам входа примыкают к rationals:
factor(sqrt(2)*x^4 - sqrt(2)*x^2 - sqrt(2)*2)
![]()
factor(I*x^4 - I*x^2 - I*2)
![]()
factor(sqrt(2)*I*x^4 - sqrt(2)*I*x^2 - sqrt(2)*I*2)
![]()
С опцией Примыкают, к дополнительным элементам можно примкнуть к подразумеваемому содействующему звонку:
factor(x^2 + 1, Adjoin = [I])
![]()
factor( x^2-2, Adjoin = {sqrt(2)} )![]()
С опцией Full, может быть вычислена полная факторизация в линейные факторы.
factor( x^2-2, Full)
![]()
Если аргумент R_ или C_ дан, факторизация сделана по вещественным или комплексным числам с помощью числовых вычислений:
factor( x^2-2, R_ )
![]()
factor(x^2 + 1, C_)
![]()
Трансцендентальные объекты обработаны как indeterminates:
delete x: factor(7*(cos(x)^2 - 1)*sin(1)^3)
![]()
Factored::factors(%), Factored::exponents(%)
![]()
factor расценивает трансцендентальные подвыражения как алгебраически независимый друг от друга. Иногда, зависимость распознана:
factor(x + 2*sqrt(x) + 1)
![]()
Во многих случаях, однако, алгебраическая зависимость не распознана:
factor(x^2 + (2^y*3^y + 6^y)* x + (6^y)^2)
![]()
factor числа с плавающей запятой замен приближениями непрерывной дроби, учитывает получившийся полином, и наконец применяет float к коэффициентам факторов:
factor(x^2 + 2.0*x - 8.0)
![]()
factor с опцией Full может использовать RootOf символически представлять корни полинома:
factor(x^5 + x^2 + 1, Full)

Полиномы с коэффициентом звонят кроме Expr учтены по их содействующему звонку. Мы учитываем следующий полином по модулю 17:
R := Dom::IntegerMod(17): f:= poly(x^3 + x + 1, R): factor(f)
![]()
Для каждого p, выражение IntMod(p) может использоваться вместо Dom::IntegerMod(p):
R := IntMod(17): f:= poly(x^3 + x + 1, R): factor(f)
![]()
Более комплексные области позволены, когда коэффициент звонит, если они могут быть получены из рациональных чисел или из конечного поля выполненной с помощью итераций конструкцией алгебраических расширений, полиномиальных звонков и полей частей. В следующем примере мы учитываем одномерный полиномиальный u 2 - x 3 в u по содействующему полю![]() :
:
Q := Dom::Rational: Qx := Dom::Fraction(Dom::DistributedPolynomial([x], Q)): F := Dom::AlgebraicExtension(Qx, poly(z^2 - x, [z])): f := poly(u^2 - x^3, [u], F)

factor(f)

| |
|
R_ или C_ |
|
Опция, заданная как Только алгебраические числа максимальной степени |
|
Опция, заданная как В дополнение к коэффициентам |
|
Опция, заданная как Вычислите числовую факторизацию |
|
Вычислите полную факторизацию |
Объект доменного типа Factored.
f
Алгоритмы факторинга собраны в отдельной области библиотеки faclib; не должно быть необходимо вызвать эти стандартные программы непосредственно.
Реализованные алгоритмы включают Cantor-Zassenhaus (по конечным полям) и Hensel, поднимающийся (по рациональным числам и в многомерном случае).
Factored | collect | content | denom | div | divide | expand | gcd | icontent | ifactor | igcd | ilcm | indets | irreducible | isprime | lcm | normal | numer | partfrac | polylib::decompose | polylib::divisors | polylib::primpart | polylib::sqrfree | rationalize | simplify