Используйте sparss и mechss объекты представлять разреженные системы второго порядка и первого порядка, соответственно. Такие разреженные модели являются результатом анализа конечных элементов (FEA) и полезны в полях как структурный анализ, поток жидкости, теплопередача и электромагнетизм. FEA включает анализ проблемы с помощью метода конечных элементов (FEM), где большая система подразделена на многочисленные, меньшие компоненты или конечные элементы (FE), которые затем анализируются отдельно. Эти многочисленные компоненты, когда объединено вместе приводят к большим разреженным моделям, которые являются в вычислительном отношении дорогими и неэффективными, чтобы быть представленными традиционными плотными объектами модели как ss.
Разреженные матрицы обеспечивают эффективное устройство хранения данных двойных или логических данных, которые имеют большой процент нулей. В то время как полный (или плотный) матрицы хранят каждый элемент в памяти независимо от значения, разреженные матрицы хранят только ненулевые элементы и их индексы строки. Поэтому использование разреженных матриц может значительно уменьшать объем памяти, требуемый для хранения данных. Для получения дополнительной информации смотрите Вычислительные Преимущества Разреженных матриц.
Следующая таблица иллюстрирует типы разреженных моделей, которые могут быть представлены:
| Тип модели | Математическое представление | Объект модели |
|---|---|---|
| Непрерывное время разреженная модель первого порядка |
| sparss |
| Дискретное время разреженная модель первого порядка |
| sparss |
| Непрерывное время разреженная модель второго порядка |
| mechss |
| Дискретное время разреженная модель второго порядка |
| mechss |
Можно использовать sparssdata и mechssdata получить доступ к матрицам модели в разреженной форме. Можно также использовать команды как spy
(sparss) и spy
(mechss) визуализировать разреженность матриц модели второго порядка и первого порядка, соответственно.
Можно также преобразовать любую non-FRD модель в a sparss или a mechss объект соответственно. С другой стороны можно использовать full команда, чтобы преобразовать разреженные модели в плотное устройство хранения данных ss. Преобразование в плотное устройство хранения данных не рекомендуется для больших разреженных моделей, когда это приводит к использованию верхней памяти и низкой производительности.
Все стандартные основанные на сигнале связи, перечисленные при Соединении моделей, поддерживаются для разреженных объектов модели. Взаимосвязанные модели с помощью сигналов позволяют вам создавать модели для систем управления. Можно представить систему управления как блок-схему, содержащую несколько взаимосвязанных компонентов, таких как объект и контроллер, подключенный в настройке обратной связи. Используя математическую модель или соединительные команды, вы комбинируете модели каждого из этих компонентов в одну модель, представляющую целую блок-схему.
Последовательно и связи обратной связи sparss модели, устраняя внутренние сигналы могут привести к нежелательной временной замене в A матрица. Чтобы предотвратить это, программное обеспечение устраняет только те сигналы, которые не влияют на разреженность A и добавляет остающиеся сигналы в вектор состояния. В общем случае это производит модель дифференциального алгебраического уравнения (DAE) соединения где A матрица имеет структуру фигурной стрелки, как изображено в следующем рисунке:
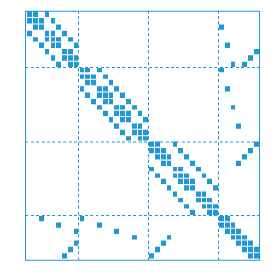
Здесь, каждый диагональный блок является субкомпонентом разреженной модели. Последняя строка и столбец комбинирует Interface и Signal группы, чтобы получить все связи и связи между компонентами.
Те же правила применяются второго порядка mechss объекты модели. Можно использовать showStateInfo распечатать сводные данные раздела вектора состояния на компоненты, интерфейсы и сигналы
Используйте xsort команда, чтобы отсортировать состояния на основе раздела состояния. В отсортированной модели все компоненты появляются первыми, сопровождаемые интерфейсами, и затем сопровождаемые одной группой всех внутренних сигналов.
Можно использовать interface команда, чтобы задать физические интерфейсы между компонентами a mechss модель. interface использует двойную формулировку блока, где глобальный набор степеней свободы (число степеней свободы) сохраняется, и блок сделан путем удовлетворения условию равновесия где g является интерфейсной силой, и λ является множителем Лагранжа. Множители Лагранжа представляют интерфейсные силы, соединяющие число степеней свободы в физическом интерфейсе. Для того, чтобы удовлетворить совместимости, второе уравнение добавляется к системе, теперь работающей со смещениями:
Для получения дополнительной информации смотрите interface и твердый блок компонентов модели.
Следующие правила приоритета применяются при объединении моделей различных типов:
Объединение разреженных моделей с моделями FRD уступает frd объект модели
Объединение разреженных моделей с любой non-FRD моделью как tf, ss, и zpk дает к разреженному объекту модели
Объединение sparss и mechss модели дают к a mechss объект модели.
В настоящее время разреженные модели не могут быть объединены с обобщенными или неопределенными моделями, genss и uss (Robust Control Toolbox).
Для примеров смотрите mechss страница с описанием.
Все стандартные аналитические функции временного интервала, перечисленные при Анализе Времени и Частотного диапазона, поддерживаются для sparss и mechss объекты модели.
Необходимо задать вектор из частот для функций частотной характеристики для разреженных моделей. Например,
tf = 10; step(sys,tf) t = 0:0.001:1; initial(sys,x0,t)
Функции отклика времени используют пользовательские решатели ДАУ фиксированного шага, которые были разработаны специально для крупномасштабных разреженных моделей. Можно сконфигурировать тип решателя ДАУ и включить параллельные вычисления при помощи SolverOptions свойство sparss и mechss объекты модели. Параллельные вычисления могут использоваться, чтобы ускориться step или impulse симуляция ответа для мультивходных моделей как ответ для каждого входного канала симулирована параллельно. Включение параллельных вычислений требует лицензии Parallel Computing Toolbox™.
Доступные опции решателя обрисованы в общих чертах в приведенной ниже таблице:
| Решатель ДАУ | Описание | Использование |
|---|---|---|
'trbdf2'[2] | Фиксированный решатель шага с точностью o(h^2), где h размер шага. 'trbdf2' является на 50% более в вычислительном отношении дорогим, чем 'hht'. Это - опция решателя ДАУ по умолчанию для обоих sparss и mechss модели. | Доступный для обоих sparss и mechss модели. |
'trbdf3' | Фиксированный решатель шага с точностью o(h^3). 'trbdf3' является на 50% более в вычислительном отношении дорогим, чем 'trbdf2'. | Доступный для обоих sparss и mechss модели. |
'hht'[1] | Фиксированный решатель шага с точностью o(h^2), где h размер шага. 'hht' является самым быстрым, но может столкнуться с трудностями с высоким начальным ускорением как импульсная характеристика системы. | Доступный для mechss модели только. |
Чтобы включить параллельные вычисления и выбор решателя, используйте следующий синтаксис:
sys.SolverOptions.UseParallel = true; sys.SolverOptions.DAESolver = 'trbdf3';
Для примера смотрите, что Переходный процесс Моделирует и Линейный Анализ Консольного Луча.
Все стандартные аналитические функции частотного диапазона, перечисленные при Анализе Времени и Частотного диапазона, поддерживаются для sparss и mechss объекты модели. Для расчетов частотной характеристики, включая параллельные вычисления ускоряет расчет ответа путем распределения набора частот через доступных рабочих. Включение параллельных вычислений требует лицензии Parallel Computing Toolbox.
Необходимо задать итоговое время или временной вектор для функций частотной характеристики для разреженных моделей. Например,
w = logspace(0,8,1000); bode(sys,w) sigma(sys,w)
Для примера смотрите, что Переходный процесс Моделирует и Линейный Анализ Консольного Луча.
Можно преобразовать между непрерывным временем и дискретным временем, и передискретизировать sparss использование моделей c2d, d2c и d2d. Следующая таблица обрисовывает в общих чертах доступные методы для sparss модели:
| Метод | Описание | Использование |
|---|---|---|
'tustin' | Билинейное приближение Тастина | Доступный с c2d, d2c и d2d функции. |
'damped' | Ослабленное приближение Тастина на основе формулы TRBDF2 [2]. Этот метод обеспечивает затухание в бесконечности в отличие от 'tustin' метод, то есть, высокочастотные движущие силы отфильтрованы и не способствуют накоплению режимов около z = -1 в дискретной модели (источник числовой нестабильности). | Доступный с c2d только. |
Примечание
В настоящее время, mechss модели не поддерживаются для непрерывных и дискретных преобразований. Преобразуйте в sparss форма модели для дискретизации.
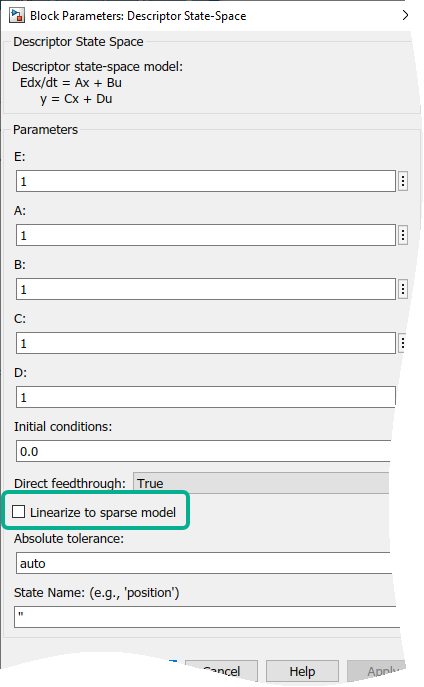
Можно получить разреженную линеаризовавшую модель из модели Simulink®, когда блок Descriptor State-Space (Simulink) или Sparse Second Order присутствует.
Блок Sparse Second Order сконфигурирован, чтобы всегда линеаризовать к a mechss модель. В результате полная линеаризовавшая модель является разреженной моделью второго порядка, когда этот блок присутствует.
Проверяйте опцию Linearize to sparse в блок Descriptor State-Space (Simulink), чтобы линеаризовать к a sparss модель. Можно также достигнуть этого путем установки LinearizerToSparse параметр к 'on' в Descriptor State-Space (Simulink). По умолчанию флажок Linearize to sparse снимается и LinearizerToSparse 'off'. Блочный уровень LinearizeToSparse установка проигнорирована, когда вы задаете замену для блока, любого с SCDBlockLinearizationSpecification параметры блоков или blocksub введите к linearize (Simulink Control Design).
Для примера смотрите, Линеаризуют Модель Simulink к Разреженному Объекту модели Второго порядка.
Кроме того, следующая функциональность в настоящее время поддерживается для разреженных моделей:
Низкочастотное использование расчета усиления dcgain
Использование оценки частотной характеристики evalfr и freqresp
Инвертирование использования моделей inv
Неявно-явное использование преобразований отношения imp2exp
Использование приближений Padé pade
Введите, выведите и внутренняя спецификация задержки
Выбор ввода-вывода и индексация
Следующие операции в настоящее время не поддержаны для разреженных моделей:
Полюс/нуль и расчет запаса устойчивости
Проект компенсатора и настройка
Сокращение порядка модели
Можно использовать full команда, чтобы преобразовать маленькие разреженные модели в плотное устройство хранения данных ss выполнять вышеупомянутые операции. Преобразование в плотное устройство хранения данных не рекомендуется для больших разреженных моделей, когда это может насыщать доступную память и вызвать серьезное ухудшение эффективности.
Нижеследующие ограничения существуют для разреженной линеаризации:
Когда вы устанавливаете linearize (Simulink Control Design) опция BlockReduction к 'off', модель всегда линеаризуется к плотному ss модель. Это вызвано тем, что блокируйтесь, замена отключена в этом случае.
Разреженная линеаризация несовместима с заменами блока, включающими настраиваемые или неопределенные модели. Опция Linearize to sparse model должна быть неконтролируема при попытке линеаризовать к genss или uss Модели (Robust Control Toolbox).
Линеаризация снимка состояния не может работать, когда блок Descriptor State-Space (Simulink) или Sparse Second Order присутствует. Поскольку линеаризация снимка состояния требует симуляции, возможности симуляции в настоящее время ограничиваются для Descriptor State-Space блоки Sparse Second Order и (Simulink).
[1] Х. Хилбер, T. Hughes & R. Тейлор. "Улучшенное числовое рассеяние для алгоритмов интегрирования времени в структурной динамике". Землетрясение Техническая и Структурная Динамика, издание 5, № 3, стр 283-292, 1977.
[2] М. Осия и Л. Шемпин. "Анализ и реализация TR-BDF2". Прикладная Числовая Математика, издание 20, № 1-2, стр 21-37, 1996.
full | getx0 | interface | mechss | mechssdata | showStateInfo | Sparse Second Order | sparss | sparssdata | spy | xsort | Descriptor State-Space (Simulink)