Сравнение предиктивной производительности после создания моделей с помощью приложения Econometric Modeler

В этом примере показано, как выбрать задержки для модели ARIMA путем сравнения значений AIC оцененных моделей с помощью приложения Econometric Modeler. В примере также показано, как сравнить прогностическую производительность нескольких моделей, которые имеют лучшие посадки в выборке в командной строке. Набор данных Data_Airline.mat содержит ежемесячные данные о пассажирах авиакомпаний.

Импорт данных в Econometric Modeler

В командной строке загрузите Data_Airline.mat набор данных.

load Data_Airline

Чтобы сравнить прогностическую производительность позже, зарезервируйте последние два года данных в качестве выборки.

fHorizon = 24;
HoldoutTable = DataTable((end - fHorizon + 1):end,:);
DataTable((end - fHorizon + 1):end,:) = [];

В командной строке откройте приложение Econometric Modeler.

econometricModeler

Можно также открыть приложение из галереи приложений (см. Econometric Modeler).

Импорт DataTable в приложение:

На вкладке Econometric Modeler в разделе Импорт щелкните значок.
В диалоговом окне «Импорт данных» в окне «Импорт»? установите флажок для DataTable переменная.
Щелкните Импорт (Import).

Переменная PSSG появляется на панели Временной ряд (Time Series), его значение появляется на панели Предварительный просмотр (Preview), а его график временных рядов появляется в окне рисунка Временной ряд (PSSG).

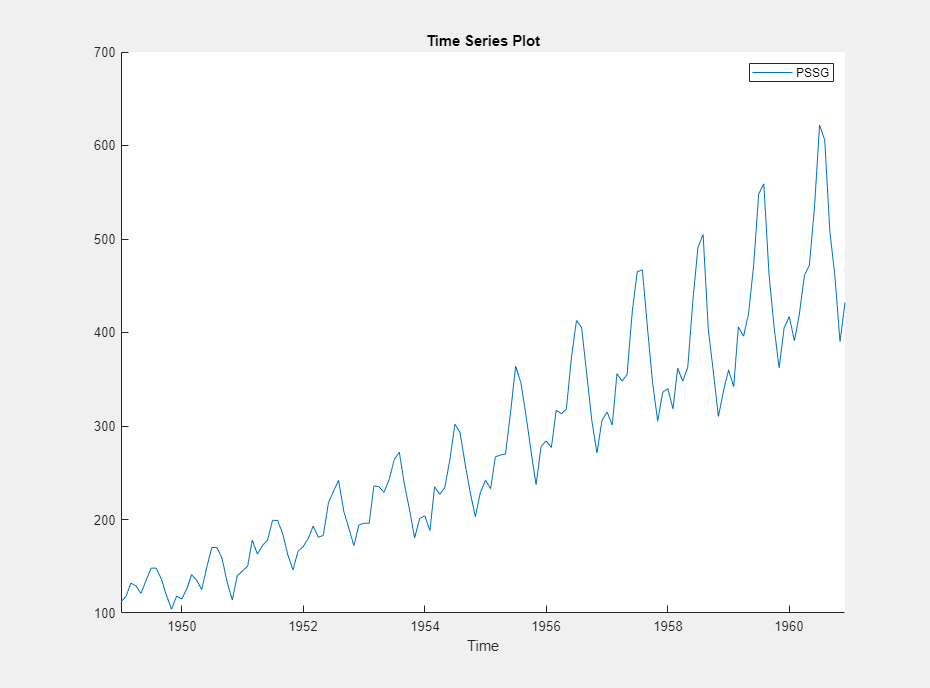
Серия демонстрирует сезонный тренд, последовательную корреляцию и возможный экспоненциальный рост. Интерактивный анализ последовательной корреляции см. в разделе Обнаружение последовательной корреляции с помощью приложения Econometric Modeler App.

Удалить экспоненциальный тренд

Устраните экспоненциальный тренд, применив преобразование журнала к PSSG.

На панели «Временные ряды» выберите PSSG.
На вкладке Econometric Modeler в разделе Преобразования щелкните Log.

Преобразованная переменная PSSGLog появляется на панели Временной ряд (Time Series), его значение появляется на панели Предварительный просмотр (Preview), а его график временных рядов появляется в окне рисунка Временной ряд (PSSGLog).

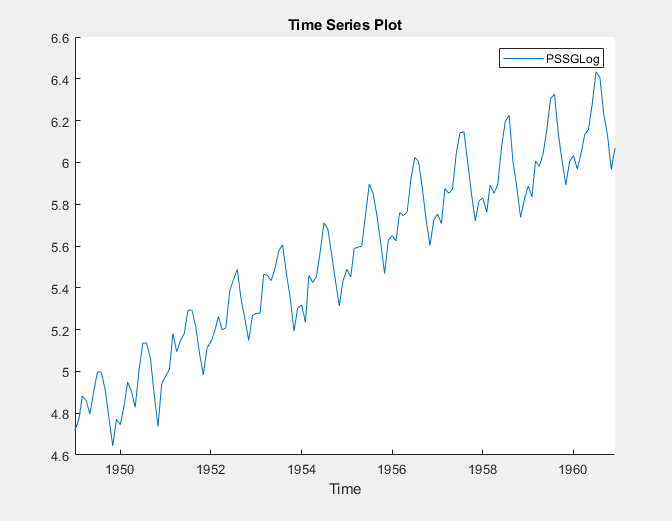
Экспоненциальный рост, по-видимому, удален из ряда.

Сравнение посадок модели в образце

Box, Jenkins и Reinsel предлагают модель SARIMA (0,1,1) × (_0,1,1) 12 без константы дляPSSGLog [1] (дополнительные сведения см. в разделе Оценка мультипликативной модели ARIMA с использованием приложения эконометрического моделирования). Тем не менее, рассмотрим все комбинации ежемесячных моделей SARIMA, которые включают до двух сезонных и несезонных задержек MA. В частности, повторите следующие шаги для каждой из девяти моделей вида SARIMA (0,1, q) × (0,1, _q12) 12, где q ∈ {0,1,2} и q12 ∈ {0,1,2}.

Для первой итерации:
1. Пусть q = q12 = 0.
2. С PSSGLog на панели Временные ряды (Time Series) щелкните вкладку Эконометрический моделирующий (Econometric Modeler). В разделе Модели (Models) щелкните стрелку, чтобы отобразить галерею моделей.
3. В коллекции моделей в разделе Модели ARMA/ARIMA щелкните SARIMA.
4. В диалоговом окне «Параметры модели SARIMA» на вкладке «Порядок задержки» выполните следующие действия.
  - Несезонная секция
    Установка степеней интеграции в 1.
    Задайте для заказа скользящего среднего значение 0.
    Снимите флажок Включить постоянный термин (Include Constant Term).
  - Сезонный участок
    Установить период в 12 для указания ежемесячных данных.
    Задайте для заказа скользящего среднего значение 0.
    Установите флажок Включить сезонную разницу.
5. Щелкните Оценка (Estimate).
Переименуйте новую переменную модели.
1. На панели Модели (Models) дважды щелкните новую переменную модели, чтобы выбрать ее имя.
2. Войти SARIMA01qx01q₁₂. Например, когда q = q₁₂ = 0, переименовать переменную в SARIMA010x010.
В сводке модели (SARIMA01qx01q₁₂) в таблице Goodness of Fit запишите значение AIC. Например, для переменной модели SARIMA010x010, AIC на этом рисунке.
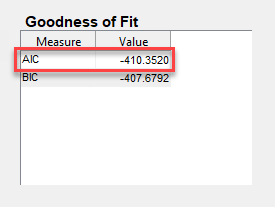
Для следующей итерации выберите значения q и q12. Например, q = 0 и q12 = 1 для второй итерации.
На панели Модели (Models) щелкните правой кнопкой мыши SARIMA01qx01q₁₂. В контекстном меню выберите «Изменить», чтобы открыть диалоговое окно «Параметры модели SARIMA» с текущими настройками для выбранной модели.
В диалоговом окне «Параметры модели SARIMA»:
1. В разделе «Несезонный» задайте для параметра «Заказ на скользящее среднее» значение q.
2. В разделе Сезонный (Seasonal) установите значение Заказ на скользящее среднее (Moving Average Order) q₁₂.
3. Щелкните Оценка (Estimate).

После выполнения шагов панель Модели (Models) содержит девять расчетных моделей с именем SARIMA010x010 через SARIMA012x012.

Полученные значения AIC представлены в этой таблице.

Модель	Имя переменной	AIC
SARIMA (0,1,0) × (_0,1,0) 12	`SARIMA010x010`	-410.3520
SARIMA (0,1,0) × (_0,1,1) 12	`SARIMA010x011`	-443.0009
SARIMA (0,1,0) × (_0,1,2) 12	`SARIMA010x012`	-441.0010
SARIMA (0,1,1) × (_0,1,0) 12	`SARIMA011x010`	-422.8680
SARIMA (0,1,1) × (_0,1,1) 12	`SARIMA011x011`	-452.0039
SARIMA (0,1,1) × (_0,1,2) 12	`SARIMA011x012`	-450.0605
SARIMA (0,1,2) × (_0,1,0) 12	`SARIMA012x010`	-420.9760
SARIMA (0,1,2) × (_0,1,1) 12	`SARIMA012x011`	-450.0087
SARIMA (0,1,2) × (_0,1,2) 12	`SARIMA012x012`	-448.0650

Три модели, дающие самые низкие три значения AIC: SARIMA (0,1,1) × (_0,1,1) 12, SARIMA (0,1,1) × _(0,1,2) 12 и SARIMA (0,1,2₎ × (0,1,1) 12. Эти модели имеют наилучшую рассудительность в образце.

Экспорт лучших моделей в рабочую область

Экспортируйте модели с наилучшими посадками в образце.

На вкладке Econometric Modeler в разделе Экспорт щелкните значок.
В диалоговом окне Экспорт переменных (Export Variables) в столбце Модели (Models) установите флажок Выбрать (Select) для SARIMA011x011, SARIMA011x012, и SARIMA012x011. Снимите флажок для любых других выбранных моделей.
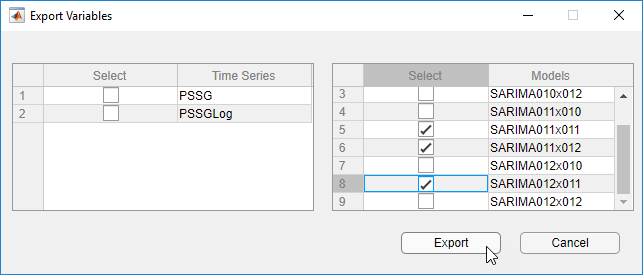
Щелкните Экспорт (Export).

arima объекты модели SARIMA011x011, SARIMA011x012, и SARIMA012x011 отображаются в рабочей области MATLAB ®.

Прогноз оценки

В командной строке оцените прогнозы на два года вперед для каждой модели.

f5 = forecast(SARIMA_PSSGLog5,fHorizon);
f6 = forecast(SARIMA_PSSGLog6,fHorizon);
f8 = forecast(SARIMA_PSSGLog8,fHorizon);

f5, f6, и f8 представляют собой векторы 24 на 1, содержащие прогнозы.

Сравнение среднеквадратических ошибок прогнозирования

Оцените среднеквадратическую ошибку прогнозирования (PMSE) для каждого из векторов прогноза.

logPSSGHO = log(HoldoutTable.Variables);
pmse5 = mean((logPSSGHO - f5).^2);
pmse6 = mean((logPSSGHO - f6).^2);
pmse8 = mean((logPSSGHO - f8).^2);

Определите модель, обеспечивающую наименьшую PMSE.

[~,bestIdx] = min([pmse5 pmse6 pmse8],[],2)

Модель SARIMA (0,1,1) × (_0,1,1) 12 выполняет лучшие функции в выборке и вне выборки.

Ссылки

[1] Бокс, Джордж Э. П., Гвилим М. Дженкинс и Грегори К. Рейнсель. Анализ временных рядов: прогнозирование и контроль. 3-й ред. Энглвуд Клиффс, Нью-Джерси: Прентис Холл, 1994.

Документация