моделировать

Моделирование коэффициентов и инноваций ковариационной матрицы байесовской векторной авторегрессионной (VAR) модели

Синтаксис

[Coeff, Sigma] = моделирование (PriorMdl)

[Coeff, Sigma] = моделирование (PriorMdl, Y)

[Coeff, Sigma] = моделирование (___, имя, значение)

Описание

[Coeff,Sigma] = simulate(PriorMdl) возвращает случайный вектор коэффициентов Coeff и случайная инновационная ковариационная матрица Sigma взяты из предыдущей байесовской модели VAR (p) PriorMdl.

пример

[Coeff,Sigma] = simulate(PriorMdl,Y) извлекает из задних распределений, полученных или обновленных путем включения данных ответа Y.

NaNs в данных указывают отсутствующие значения, которые simulate удаляет, используя удаление по списку.

пример

[Coeff,Sigma] = simulate(___,Name,Value) указывает параметры, использующие один или несколько аргументов пары имя-значение в дополнение к любой из комбинаций входных аргументов в предыдущих синтаксисах. Например, можно задать количество случайных розыгрышей из распределения или указать данные предварительного анализа.

Примеры

свернуть все

Рисование коэффициентов и инноваций Ковариационная матрица из предыдущего распределения

Открыть сценарий в реальном времени

Рассмотрим модель 3-D VAR (4) для инфляции в США (INFL), безработица (UNRATE) и федеральные средства (FEDFUNDS) ставки.

$[\begin{array}{llllllllllllllllllll} _{} \\ _{} \\ _{} \end{array}_{}^{}_{} \begin{array}{llllllllllllllllllll} _{} \\ _{} \\ _{} \end{array} \begin{array}{cccccccccccccccccccc} _{} \\ _{} \\ _{INFLtUNRATEtFEDFUNDSt]=c+∑j=14Φj[INFLt-jUNRATEt-jFEDFUNDSt-j]+[ε1,tε2,tε3,t} \end{array}].$

Для всех $t$ $_{αt}$ - это ряд независимых 3-D нормальных нововведений со средним значением 0 и ковариацией $Λ$ . Предположим, что поведение ${_{}_{}}^{}$ параметров регулирует сопряженное предварительное распределение δ ([Ф1,..., Φ4, с] ′, Λ).

Создайте сопряженную предыдущую модель. Укажите имена серий ответов. Получить резюме предыдущего распространения.

seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
numseries = numel(seriesnames);
numlags = 4;

PriorMdl = bayesvarm(numseries,numlags,'ModelType','conjugate',...
    'SeriesNames',seriesnames);
Summary = summarize(PriorMdl,'off');

Нарисуйте набор коэффициентов и инновационную ковариационную матрицу из предыдущего распределения.

rng(1) % For reproducibility
[Coeff,Sigma] = simulate(PriorMdl);

Отображение выбранных коэффициентов с соответствующими именами и новой ковариационной матрицей.

table(Coeff,'RowNames',Summary.CoeffMap)

ans=39×1 table
                     Coeff   
                   __________

    AR{1}(1,1)        0.44999
    AR{1}(1,2)       0.047463
    AR{1}(1,3)      -0.042106
    AR{2}(1,1)     -0.0086264
    AR{2}(1,2)       0.034049
    AR{2}(1,3)      -0.058092
    AR{3}(1,1)      -0.015698
    AR{3}(1,2)      -0.053203
    AR{3}(1,3)      -0.031138
    AR{4}(1,1)       0.036431
    AR{4}(1,2)      -0.058279
    AR{4}(1,3)       -0.02195
    Constant(1)        -1.001
    AR{1}(2,1)      -0.068182
    AR{1}(2,2)        0.51029
    AR{1}(2,3)      -0.094367
      ⋮

AR {r} (j, k) - коэффициент отклика AR переменной k (запаздывающих r единиц) в уравнении ответа j.

Sigma

Sigma = 3×3

    0.1238   -0.0053   -0.0369
   -0.0053    0.0456    0.0160
   -0.0369    0.0160    0.1039

Строки и столбцы Sigma соответствуют нововведениям в уравнениях ответа, упорядоченных по PriorMdl.SeriesNames.

Моделирование параметров из аналитически отслеживаемого заднего распределения

Открыть сценарий в реальном времени

Рассмотрим модель 3-D VAR (4) ковариационной матрицы коэффициентов вытяжки и инноваций из предыдущего распределения. В этом случае предположим, что предыдущее распределение является диффузным.

Загрузка и предварительная обработка данных

Загрузить набор макроэкономических данных США. Вычислите уровень инфляции, стабилизируйте уровень безработицы и федеральные фонды и удалите недостающие значения.

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];

DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);
rmDataTable = rmmissing(DataTable);

Создать предыдущую модель

Создайте диффузную байесовскую модель VAR (4) для трех серий ответов. Укажите имена серий ответов.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = bayesvarm(numseries,numlags,'SeriesNames',seriesnames);

Оценка заднего распределения

Оцените апостериорное распределение. Возвращает сводку оценки.

[PosteriorMdl,Summary] = estimate(PriorMdl,rmDataTable{:,seriesnames});

Bayesian VAR under diffuse priors
Effective Sample Size:          197
Number of equations:            3
Number of estimated Parameters: 39
             |   Mean     Std  
-------------------------------
 Constant(1) |  0.1007  0.0832 
 Constant(2) | -0.0499  0.0450 
 Constant(3) | -0.4221  0.1781 
 AR{1}(1,1)  |  0.1241  0.0762 
 AR{1}(2,1)  | -0.0219  0.0413 
 AR{1}(3,1)  | -0.1586  0.1632 
 AR{1}(1,2)  | -0.4809  0.1536 
 AR{1}(2,2)  |  0.4716  0.0831 
 AR{1}(3,2)  | -1.4368  0.3287 
 AR{1}(1,3)  |  0.1005  0.0390 
 AR{1}(2,3)  |  0.0391  0.0211 
 AR{1}(3,3)  | -0.2905  0.0835 
 AR{2}(1,1)  |  0.3236  0.0868 
 AR{2}(2,1)  |  0.0913  0.0469 
 AR{2}(3,1)  |  0.3403  0.1857 
 AR{2}(1,2)  | -0.0503  0.1647 
 AR{2}(2,2)  |  0.2414  0.0891 
 AR{2}(3,2)  | -0.2968  0.3526 
 AR{2}(1,3)  |  0.0450  0.0413 
 AR{2}(2,3)  |  0.0536  0.0223 
 AR{2}(3,3)  | -0.3117  0.0883 
 AR{3}(1,1)  |  0.4272  0.0860 
 AR{3}(2,1)  | -0.0389  0.0465 
 AR{3}(3,1)  |  0.2848  0.1841 
 AR{3}(1,2)  |  0.2738  0.1620 
 AR{3}(2,2)  |  0.0552  0.0876 
 AR{3}(3,2)  | -0.7401  0.3466 
 AR{3}(1,3)  |  0.0523  0.0428 
 AR{3}(2,3)  |  0.0008  0.0232 
 AR{3}(3,3)  |  0.0028  0.0917 
 AR{4}(1,1)  |  0.0167  0.0901 
 AR{4}(2,1)  |  0.0285  0.0488 
 AR{4}(3,1)  | -0.0690  0.1928 
 AR{4}(1,2)  | -0.1830  0.1520 
 AR{4}(2,2)  | -0.1795  0.0822 
 AR{4}(3,2)  |  0.1494  0.3253 
 AR{4}(1,3)  |  0.0067  0.0395 
 AR{4}(2,3)  |  0.0088  0.0214 
 AR{4}(3,3)  | -0.1372  0.0845 
       Innovations Covariance Matrix       
           |   INFL     DUNRATE  DFEDFUNDS 
-------------------------------------------
 INFL      |  0.3028   -0.0217     0.1579  
           | (0.0321)  (0.0124)   (0.0499) 
 DUNRATE   | -0.0217    0.0887    -0.1435  
           | (0.0124)  (0.0094)   (0.0283) 
 DFEDFUNDS |  0.1579   -0.1435     1.3872  
           | (0.0499)  (0.0283)   (0.1470)

PosteriorMdl является conjugatebvarm модель, которая аналитически прослеживается.

Моделирование параметров из задней части

Извлеките 1000 образцов из заднего распределения.

rng(1)
[Coeff,Sigma] = simulate(PosteriorMdl,'NumDraws',1000);

Coeff является матрицей случайного построения коэффициентов 39 на 1000. Каждый столбец является отдельным розыгрышем, а каждая строка - индивидуальным коэффициентом. Sigma множество случайным образом оттянутых инновационных ковариационных матриц 3 на 3 на 1000. Каждая страница является отдельным розыгрышем.

Отображение первого коэффициента, взятого из распределения с соответствующими именами параметров, и отображение первой нарисованной ковариационной матрицы нововведений.

Coeffs = table(Coeff(:,1),'RowNames',Summary.CoeffMap)

Coeffs=39×1 table
                     Var1   
                   _________

    AR{1}(1,1)       0.14994
    AR{1}(1,2)      -0.46927
    AR{1}(1,3)      0.088388
    AR{2}(1,1)       0.28139
    AR{2}(1,2)      -0.19597
    AR{2}(1,3)      0.049222
    AR{3}(1,1)        0.3946
    AR{3}(1,2)      0.081871
    AR{3}(1,3)      0.002117
    AR{4}(1,1)       0.13514
    AR{4}(1,2)      -0.23661
    AR{4}(1,3)      -0.01869
    Constant(1)     0.035787
    AR{1}(2,1)     0.0027895
    AR{1}(2,2)       0.62382
    AR{1}(2,3)      0.053232
      ⋮

Sigma(:,:,1)

ans = 3×3

    0.2653   -0.0075    0.1483
   -0.0075    0.1015   -0.1435
    0.1483   -0.1435    1.5042

Моделирование параметров из аналитически неразрешимого заднего распределения

Открыть сценарий в реальном времени

Загрузка и предварительная обработка данных

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];

DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);
rmDataTable = rmmissing(DataTable);

Создать предыдущую модель

Создайте предшествующую модель Bayesian VAR (4) для трех серий ответов. Укажите имена переменных ответа.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = bayesvarm(numseries,numlags,'Model','semiconjugate',...
    'SeriesNames',seriesnames);

Моделирование параметров из задней части

Поскольку совместное заднее распределение предшествующей модели в полунъюгате является аналитически труднореализуемым, simulate последовательно черпает из полных условных распределений.

Извлеките 1000 образцов из заднего распределения. Укажите период горения 10000 и коэффициент прореживания 5. Запустите пробоотборник Гиббса, предположив, что заднее среднее $Δ$ является матрицей тождества 3-D.

rng(1)
[Coeff,Sigma] = simulate(PriorMdl,rmDataTable{:,seriesnames},...
    'NumDraws',1000,'BurnIn',1e4,'Thin',5,'Sigma0',eye(3));

Моделирование коэффициентов из модели VARX

Открыть сценарий в реальном времени

Рассмотрим модель 2-D VARX (1) для реального ВВП США (RGDP) и инвестиции (GCE) ставки, которые лечат личное потребление (PCEC) скорость как экзогенная:

$\begin{array}{llllllllllllllllllll} _{} \\ _{} \end{array} \begin{array}{llllllllllllllllllll} _{} \\ _{} \end{array}_{}_{[RGDPtGCEt] =c +Φ [RGDPt-1GCEt-1] +PCECtβ +εt} .$

Для всех $t$ $_{αt}$ - это ряд независимых 2-D нормальных нововведений со средним значением 0 и ковариацией $Λ$ . Предположим следующие предыдущие распределения:

${\begin{array}{c} \end{array} [Φcβ]}^{'} |Σ_{∼Ν4×2} (Μ, V, Σ$ ), где M - матрица средств 4 на 2 и V, является матрицей масштаба среди коэффициента 4 на 4. Эквивалентно, $vec {\begin{array}{c} ( & [ \end{array}}^{Фсβ}]')_{} |Σ∼Ν8 (vec (Λ)$ , Σ⊗ V).
$Σ∼InverseWishart (Λ, start$ ), где Λ - матрица шкалы 2 на 2, а start- степени свободы.

Загрузить набор макроэкономических данных США. Вычислите реальные ряды показателей ВВП, инвестиций и личного потребления. Удалите все отсутствующие значения из результирующего ряда.

load Data_USEconModel
DataTable.RGDP = DataTable.GDP./DataTable.GDPDEF;
seriesnames = ["PCEC"; "RGDP"; "GCE"];
rates = varfun(@price2ret,DataTable,'InputVariables',seriesnames);
rates = rmmissing(rates);
rates.Properties.VariableNames = seriesnames;

Создайте сопряженную предыдущую модель для параметров модели 2-D VARX (1).

numseries = 2;
numlags = 1;
numpredictors = 1;
PriorMdl = conjugatebvarm(numseries,numlags,'NumPredictors',numpredictors,...
    'SeriesNames',seriesnames(2:end));

Имитировать непосредственно из заднего распределения. Укажите данные экзогенного предиктора.

[Coeff,Sigma] = simulate(PriorMdl,rates{:,PriorMdl.SeriesNames},...
    'X',rates{:,seriesnames(1)});

По умолчанию simulate использует первые p = 1 наблюдения данных ответа для инициализации динамического компонента модели и удаляет соответствующие наблюдения из данных предиктора.

Входные аргументы

свернуть все

`PriorMdl` - Предыдущая байесовская модель VAR
`conjugatebvarm` объект модели | `semiconjugatebvarm` объект модели | `diffusebvarm` объект модели | `normalbvarm` объект модели

Предыдущая байесовская модель VAR, заданная как объект модели в этой таблице.

Объект модели	Описание
`conjugatebvarm`	Зависимая, матрица-нормаль-обратная-сопряженная модель Вишарта, возвращаемая `bayesvarm` или `conjugatebvarm`
`semiconjugatebvarm`	Независимая, нормальная, обратная, полуконъюгатная предыдущая модель Вишарта, возвращенная `bayesvarm` или `semiconjugatebvarm`
`diffusebvarm`	Диффузная предыдущая модель, возвращенная `bayesvarm` или `diffusebvarm`
`normalbvarm`	Нормальная сопряженная модель с фиксированной ковариационной матрицей инноваций, возвращаемой `bayesvarm` или `normalbvarm`

Примечание

Если PriorMdl является diffusebvarm модель, затем необходимо также предоставить Y потому что simulate невозможно извлечь из неправильного предыдущего распространения. Следовательно, Coeff и Sigma представляют собой розыгрыши из заднего распределения.

`Y` - Наблюдаемый многомерный ряд ответов
числовая матрица

Наблюдаемые многомерные серии ответов, на которые simulate подходит для модели, указанной как numobsоколо-numseries числовая матрица.

numobs - размер выборки. numseries - количество переменных ответа (PriorMdl.NumSeries).

Строки соответствуют наблюдениям, а последняя строка содержит последнее наблюдение. Столбцы соответствуют отдельным переменным ответа.

Y представляет продолжение последовательности ответов предварительной выборки в Y0.

Типы данных: double

Аргументы пары «имя-значение»

Укажите дополнительные пары, разделенные запятыми Name,Value аргументы. Name является именем аргумента и Value - соответствующее значение. Name должен отображаться внутри кавычек. Можно указать несколько аргументов пары имен и значений в любом порядке как Name1,Value1,...,NameN,ValueN.

Пример: 'Y0',Y0,'X',X задает данные ответа на предварительную выборку Y0 для инициализации модели VAR для апостериорной оценки и данных предиктора X для экзогенного регрессионного компонента.

Опции для всех предыдущих дистрибутивов

свернуть все

`'NumDraws'` - Количество случайных розыгрышей
`1` (по умолчанию) | положительное целое число

Число случайных вытягиваний из распределений, указанных как пара, разделенная запятыми, состоящая из 'NumDraws' и положительное целое число.

Пример: 'NumDraws',1e7

Типы данных: double

`'Y0'` - Предварительные данные ответа
числовая матрица

Предварительные данные ответа для инициализации модели VAR для оценки, указанной как пара, разделенная запятыми, состоящая из 'Y0' и numpreobsоколо-numseries числовая матрица. numpreobs - количество предварительных наблюдений.

Строки соответствуют предварительным наблюдениям, а последняя строка содержит последнее наблюдение. Y0 должен иметь по крайней мере PriorMdl.P строк. Если указано больше строк, чем необходимо, simulate использует последние PriorMdl.P только наблюдения.

Столбцы должны соответствовать ряду ответов в Y.

По умолчанию simulate использование Y(1:PriorMdl.P,:) в качестве предварительных наблюдений, а затем оценивает задний, используя Y((PriorMdl.P + 1):end,:). Это действие уменьшает эффективный размер выборки.

Типы данных: double

`'X'` - Данные предиктора
числовая матрица

Данные предиктора для экзогенного компонента регрессии в модели, указанного как пара, разделенная запятыми, состоящая из 'X' и numobsоколо-PriorMdl.NumPredictors числовая матрица.

Строки соответствуют наблюдениям, а последняя строка содержит последнее наблюдение. simulate не использует компонент регрессии в предварительном периоде. X должно иметь по крайней мере столько наблюдений, сколько использовалось после периода предварительного отбора.

При указании Y0, то X должен иметь по крайней мере numobs строки (см. Y).
В противном случае X должен иметь по крайней мере numobs – PriorMdl.P для учета удаления предварительного образца.

В любом случае, если указано больше строк, чем необходимо, simulate использует только последние наблюдения.

Столбцы соответствуют отдельным переменным предиктора. Все переменные предиктора присутствуют в регрессионной составляющей каждого уравнения ответа.

Типы данных: double

Опции для полуконъюгации предыдущих распределений

свернуть все

`'BurnIn'` - Количество розыгрышей, снимаемых с начала пробы
`0` (по умолчанию) | неотрицательный скаляр

Количество вытягиваний, удаляемых из начала образца для уменьшения переходных эффектов, указанное как пара, разделенная запятыми, состоящая из 'BurnIn' и неотрицательный скаляр. Для получения подробной информации о том, как simulate сокращает полную выборку, см. Алгоритмы.

Совет

Чтобы помочь определить соответствующий размер периода записи, выполните следующие действия.

Определите степень переходного поведения в образце, указав 'BurnIn',0.
Моделирование нескольких тысяч наблюдений с помощью simulate.
Нарисуйте графики трассировки.

Пример: 'BurnIn',0

Типы данных: double

`'Thin'` - Множитель скорректированного размера выборки
`1` (по умолчанию) | положительное целое число

Множитель скорректированного размера выборки, указанный как пара, разделенная запятыми, состоящая из 'Thin' и положительное целое число.

Фактический размер выборки: BurnIn + NumDraws*Thin. После выгорания, simulate отбрасывает каждый Thin – 1 рисует, а затем сохраняет следующий розыгрыш. Дополнительные сведения о том, как simulate сокращает полную выборку, см. Алгоритмы.

Совет

Чтобы уменьшить потенциальную большую последовательную корреляцию в выборке или уменьшить потребление памяти для розыгрышей, хранящихся в Coeff и Sigma, укажите большое значение для Thin.

Пример: 'Thin',5

Типы данных: double

`'Coeff0'` - Начальное значение коэффициентов модели VAR для пробоотборника Гиббса
числовой вектор столбца

Начальное значение коэффициентов модели VAR для дискретизатора Гиббса, указанное как пара, разделенная запятыми, состоящая из 'Coeff0' и вектор числового столбца с (PriorMdl.NumSeries*kоколо-NumDraws элементы, где k = PriorMdl.NumSeries*PriorMdl.P + PriorMdl.IncludeIntercept + PriorMdl.IncludeTrend + PriorMdl.NumPredictors, которое является числом коэффициентов в уравнении отклика. Для получения подробной информации о структуре Coeff0, см. выходные данные Coeff.

По умолчанию Coeff0 - многомерная оценка наименьших квадратов.

Совет

Определить Coeff0:
1. Установите отдельные переменные для начальных значений каждой матрицы коэффициентов и вектора.
2. Горизонтально соединить все коэффициенты означает в следующем порядке:
  
  $\begin{matrix} _{} & _{} & _{} & Coeff=[Φ1Φ2⋯ΦpcδΒ \end{matrix}].$
3. Векторизируйте транспонирование матрицы среднего коэффициента.
  Coeff0 = Coeff.'; Coeff0 = Coeff0(:);
Хорошей практикой является запуск simulate несколько раз с различными начальными значениями параметров. Убедитесь, что оценки из каждого прогона сходятся к аналогичным значениям.

Типы данных: double

`'Sigma0'` - Начальное значение ковариационной матрицы инноваций для семплера Гиббса
положительная определенная числовая матрица

Начальное значение новой ковариационной матрицы для семплера Гиббса, указанной как пара, разделенная запятыми, состоящая из 'Sigma0' и PriorMdl.NumSeriesоколо-PriorMdl.NumSeries положительная определенная числовая матрица. По умолчанию Sigma0 - остаточная среднеквадратичная ошибка из многомерных наименьших квадратов. Строки и столбцы соответствуют нововведениям в уравнениях переменных ответа, упорядоченных по PriorMdl.SeriesNames.

Совет

Хорошей практикой является запуск simulate несколько раз с различными начальными значениями параметров. Убедитесь, что оценки из каждого прогона сходятся к аналогичным значениям.

Типы данных: double

Выходные аргументы

свернуть все

`Coeff` - Смоделированные коэффициенты модели VAR
числовая матрица

Смоделированные коэффициенты модели VAR, возвращенные как (PriorMdl.NumSeries*kоколо-NumDraws числовая матрица, где k = PriorMdl.NumSeries*PriorMdl.P + PriorMdl.IncludeIntercept + PriorMdl.IncludeTrend + PriorMdl.NumPredictors, которое является числом коэффициентов в уравнении отклика. Каждый столбец является отдельным розыгрышем из распределения.

Для розыгрыша j, Coeff(1:k,j) соответствует всем коэффициентам в уравнении переменной отклика PriorMdl.SeriesNames(1), Coeff((k + 1):(2*k),j) соответствует всем коэффициентам в уравнении переменной отклика PriorMdl.SeriesNames(2)и так далее. Для набора индексов, соответствующих уравнению:

Элементы 1 через PriorMdl.NumSeries соответствуют коэффициентам AR с запаздыванием 1 для переменных ответа, упорядоченных по PriorMdl.SeriesNames.
Элементы PriorMdl.NumSeries + 1 через 2*PriorMdl.NumSeries соответствуют коэффициентам AR с запаздыванием 2 для переменных ответа, упорядоченных по PriorMdl.SeriesNames.
В общем, элементы (q – 1)*PriorMdl.NumSeries + 1 через q*PriorMdl.NumSeries соответствуют запаздыванию q Коэффициенты AR переменных ответа упорядочены по PriorMdl.SeriesNames.
Если PriorMdl.IncludeConstant является true, элемент PriorMdl.NumSeries*PriorMdl.P + 1 - константа модели.
Если PriorMdl.IncludeTrend является true, элемент PriorMdl.NumSeries*PriorMdl.P + 2 - коэффициент линейного временного тренда.
Если PriorMdl.NumPredictors > 0, элементы PriorMdl.NumSeries*PriorMdl.P + 3 через k составляют вектор коэффициентов регрессии экзогенных переменных.

На этом рисунке показана структура Coeff(L,j) для модели 2-D VAR (3), которая содержит постоянный вектор и четыре экзогенных предиктора.

$[\overset{_{ϕ1,11ϕ1,12ϕ2,11ϕ2,12ϕ3,11ϕ3,12c1β11β12β13β14︷y1,t}}{\overset{}{\begin{matrix} _{} & _{} & _{} & _{} & _{} & _{} & _{} & _{} & _{} & _{} & _{} \end{matrix}}} \overset{_{ϕ1,21ϕ1,22ϕ2,21ϕ2,22ϕ3,21ϕ3,22c2β21β22β23β24︷y2,t}}{\overset{}{\begin{matrix} _{} & _{} & _{} & _{} & _{} & _{} & _{} & _{} & _{} & _{} & _{} \end{matrix}}}],$

где

β q_{, jk} - элемент (j, k) матрицы коэффициентов lag q AR.
cj - константа модели в уравнении переменной отклика j.
Bju - коэффициент регрессии экзогенной переменной u в уравнении переменной ответа j.

`Sigma` - Смоделированные ковариационные матрицы инноваций
массив положительных определенных числовых матриц

Смоделированные инновации ковариационные матрицы, возвращенные как PriorMdl.NumSeriesоколо-PriorMdl.NumSeriesоколо-NumDraws массив положительных определенных числовых матриц.

Каждая страница представляет собой отдельный розыгрыш (ковариацию) от дистрибутива. Строки и столбцы соответствуют нововведениям в уравнениях переменных ответа, упорядоченных по PriorMdl.SeriesNames.

Если PriorMdl является normalbvarm объект, все ковариации в Sigma равны PriorMdl.Covariance.

Ограничения

simulate невозможно извлечь значения из неправильного распределения, которое является распределением, плотность которого не интегрирована в 1.

Подробнее

свернуть все

Модель авторегрессии байесовского вектора (VAR)

Байесовская модель VAR рассматривает все коэффициенты и инновационную ковариационную матрицу как случайные величины в m-мерной стационарной модели VARX (p). Модель имеет одну из трех форм, описанных в этой таблице.

Модель	Уравнение
VAR (p) редуцированной формы в нотации разностного уравнения	$_{yt} =_{}_{Φ1yt} − 1 +_{.} ._{. +} Фpyt -_{p} +_{} c$ + δt + Βxt + αt.
Многомерная регрессия	$_{yt} =_{} {Ztλ}_{} +$ αt.
Регрессия матрицы	$_{}^{}_{}^{}_{yt=Λ′zt′+εt} .$

Для каждого времени t = 1,...,T:

_yt - m-мерный наблюдаемый вектор отклика, где m = numseries.
_Φ1,...,Φp - матрицы коэффициентов m-by-m AR лагов 1-p, где p =numlags.
c - вектор m-by-1 констант модели, если IncludeConstant является true.
δ - вектор m-на-1 коэффициентов линейного тренда времени, если IncludeTrend является true.
Β - матрица коэффициентов регрессии вектора r-by-1 наблюдаемых экзогенных предикторов xt, где r = NumPredictors. Все переменные предиктора появляются в каждом уравнении.
$_{} \begin{matrix} _{}^{} & _{}^{} & _{}^{} & _{zt=[yt−1′yt−2′⋯yt−p′1txt}^{} \end{matrix}']$ , который является вектором 1-by- (mp + r + 2), а Zt является диагональной матрицей m-by-m (mp + r + 2)

$\begin{matrix} _{} & _{} & _{} \\ _{} & _{} & _{} \\ _{} & _{} & _{} & _{} \end{matrix} [zt0z0z0zzt0z 0z0z0zzt],$
где _0z - 1-по- (мп + r + 2) вектор нулей.
${\begin{matrix} _{} & _{} & _{} & Λ=[Φ1Φ2⋯ΦpcδΒ \end{matrix}]}^{}$ ′, которая является случайной матрицей коэффициентов (mp + r + 2) -by-m, а m (mp + r + 2) -by-1 вектором λ = vec (Λ).
_{δ t} - вектор m-на-1 случайных, последовательно некоррелированных, многомерных нормальных нововведений с нулевым вектором для среднего и матрицей m-на-м для ковариации. Это предположение подразумевает, что вероятность данных

$ℓ (Λ,Σ'y, x)_{=}^{} {∏t=1Tf}_{} (yt; Λ_{,Σ},$ zt),
где f - m-мерная многомерная нормальная плотность со средним значением ztΛ и ковариацией

Прежде, чем рассмотреть данные, Вы налагаете совместное предшествующее предположение распределения на (Λ,Σ), которым управляет распределение π (Λ,Σ). В байесовском анализе распределение параметров обновляется информацией о параметрах, полученных из правдоподобия данных. В результате получается совместное заднее распределение λ (Λ, Λ 'Y, X, _Y0), где:

Y представляет собой матрицу T-на-m, содержащую весь ответный ряд {yt}, t = 1,...,T.
X представляет собой матрицу T-на-m, содержащую весь экзогенный ряд {xt}, t = 1,...,T.
Y0 является p-by-m матрицей предварительных данных, используемых для инициализации модели VAR для оценки.

Совет

Моделирование Монте-Карло подвержено изменению. Если simulate использует моделирование Монте-Карло, тогда оценки и выводы могут различаться при вызове simulate многократно при, казалось бы, эквивалентных условиях. Чтобы воспроизвести результаты оценки, установите начальное число случайного числа с помощью rng перед вызовом simulate.

Алгоритмы

Если simulate оценивает апостериорное распределение (при поставке Y) и задняя является аналитически отслеживаемой, simulate моделируется непосредственно с задней стороны. В противном случае simulate использует пробоотборник Гиббса для оценки заднего.
На этом рисунке показано, как simulate уменьшает выборку, используя значения NumDraws, Thin, и BurnIn. Прямоугольники представляют последовательные розыгрыши из распределения. simulate удаляет белые прямоугольники из образца. Остающееся NumDraws образец составляют черные прямоугольники.
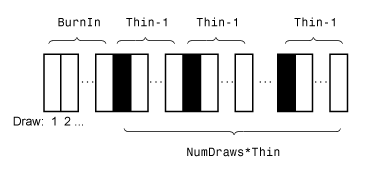
Если PriorMdl является semiconjugatebvarm и не указываете начальные значения (Coeff0 и Sigma0), simulate образцы из заднего распределения путем применения образца Гиббса.
1. simulate использует значение по умолчанию Sigma0 для Σ и тянет ценность Λ от π (Λ 'Σ, Y, X), полное условное распределение коэффициентов модели VAR.
2. simulate рисует значение Λ из δ (Λ 'Λ, Y, X), полного условного распределения ковариационной матрицы нововведений, используя ранее сгенерированное значение Λ.
3. Функция повторяет шаги 1 и 2 до сходимости. Чтобы оценить сходимость, нарисуйте график трассировки образца.
При указании Coeff0, simulate тянет ценность Σ от π (Σ 'Λ, Y, X), чтобы начать образец Гиббса.
simulate не возвращает созданные по умолчанию начальные значения.

См. также

Объекты

conjugatebvarm | diffusebvarm | empiricalbvarm | normalbvarm | semiconjugatebvarm

Документация

моделировать

Синтаксис

Описание

Примеры

Рисование коэффициентов и инноваций Ковариационная матрица из предыдущего распределения

Моделирование параметров из аналитически отслеживаемого заднего распределения

Моделирование параметров из аналитически неразрешимого заднего распределения

Моделирование коэффициентов из модели VARX

Входные аргументы

`PriorMdl` - Предыдущая байесовская модель VAR
`conjugatebvarm` объект модели | `semiconjugatebvarm` объект модели | `diffusebvarm` объект модели | `normalbvarm` объект модели

`Y` - Наблюдаемый многомерный ряд ответов
числовая матрица

Аргументы пары «имя-значение»

`'NumDraws'` - Количество случайных розыгрышей
`1` (по умолчанию) | положительное целое число

`'Y0'` - Предварительные данные ответа
числовая матрица

`'X'` - Данные предиктора
числовая матрица

`'BurnIn'` - Количество розыгрышей, снимаемых с начала пробы
`0` (по умолчанию) | неотрицательный скаляр

`'Thin'` - Множитель скорректированного размера выборки
`1` (по умолчанию) | положительное целое число

`'Coeff0'` - Начальное значение коэффициентов модели VAR для пробоотборника Гиббса
числовой вектор столбца

`'Sigma0'` - Начальное значение ковариационной матрицы инноваций для семплера Гиббса
положительная определенная числовая матрица

Выходные аргументы

`Coeff` - Смоделированные коэффициенты модели VAR
числовая матрица

`Sigma` - Смоделированные ковариационные матрицы инноваций
массив положительных определенных числовых матриц

Ограничения

Подробнее

Модель авторегрессии байесовского вектора (VAR)

Совет

Алгоритмы

См. также

Объекты

Функции

Документация по инструментарию Econometrics

Поддержка

Документация

моделировать

Синтаксис

Описание

Примеры

Рисование коэффициентов и инноваций Ковариационная матрица из предыдущего распределения

Моделирование параметров из аналитически отслеживаемого заднего распределения

Моделирование параметров из аналитически неразрешимого заднего распределения

Моделирование коэффициентов из модели VARX

Входные аргументы

PriorMdl - Предыдущая байесовская модель VAR conjugatebvarm объект модели | semiconjugatebvarm объект модели | diffusebvarm объект модели | normalbvarm объект модели

Y - Наблюдаемый многомерный ряд ответов числовая матрица

Аргументы пары «имя-значение»

'NumDraws' - Количество случайных розыгрышей 1 (по умолчанию) | положительное целое число

'Y0' - Предварительные данные ответа числовая матрица

'X' - Данные предиктора числовая матрица

'BurnIn' - Количество розыгрышей, снимаемых с начала пробы 0 (по умолчанию) | неотрицательный скаляр

'Thin' - Множитель скорректированного размера выборки 1 (по умолчанию) | положительное целое число

'Coeff0' - Начальное значение коэффициентов модели VAR для пробоотборника Гиббса числовой вектор столбца

'Sigma0' - Начальное значение ковариационной матрицы инноваций для семплера Гиббса положительная определенная числовая матрица

Выходные аргументы

Coeff - Смоделированные коэффициенты модели VAR числовая матрица

Sigma - Смоделированные ковариационные матрицы инноваций массив положительных определенных числовых матриц

Ограничения

Подробнее

Модель авторегрессии байесовского вектора (VAR)

Совет

Алгоритмы

См. также

Объекты

Функции

Документация по инструментарию Econometrics

Поддержка

`PriorMdl` - Предыдущая байесовская модель VAR
`conjugatebvarm` объект модели | `semiconjugatebvarm` объект модели | `diffusebvarm` объект модели | `normalbvarm` объект модели

`Y` - Наблюдаемый многомерный ряд ответов
числовая матрица

`'NumDraws'` - Количество случайных розыгрышей
`1` (по умолчанию) | положительное целое число

`'Y0'` - Предварительные данные ответа
числовая матрица

`'X'` - Данные предиктора
числовая матрица

`'BurnIn'` - Количество розыгрышей, снимаемых с начала пробы
`0` (по умолчанию) | неотрицательный скаляр

`'Thin'` - Множитель скорректированного размера выборки
`1` (по умолчанию) | положительное целое число

`'Coeff0'` - Начальное значение коэффициентов модели VAR для пробоотборника Гиббса
числовой вектор столбца

`'Sigma0'` - Начальное значение ковариационной матрицы инноваций для семплера Гиббса
положительная определенная числовая матрица

`Coeff` - Смоделированные коэффициенты модели VAR
числовая матрица

`Sigma` - Смоделированные ковариационные матрицы инноваций
массив положительных определенных числовых матриц