Временной ряд yt представляет собой совокупность наблюдений по переменной, индексированной последовательно в нескольких временных точках t = 1, 2,...,T. Наблюдения временных рядов y1, y2,...,yT по своей сути зависят. С точки зрения статистического моделирования это означает, что неуместно рассматривать временной ряд как случайную выборку независимых наблюдений.
Цель статистического моделирования - найти компактное представление процесса генерации данных для данных. Статистический строительный блок эконометрического моделирования временных рядов является стохастическим процессом. Эвристически стохастический процесс является совместным распределением вероятности для набора случайных величин. Моделируя наблюдаемый временной ряд yt как реализацию из стохастического процесса .., T}, можно приспособить высокоразмерный и зависимый характер данных. Набор времен наблюдения Т может быть дискретным или непрерывным. Рисунок 1-1, Среднемесячный CO2 показывает среднемесячную концентрацию CO2 (ppm), зарегистрированную обсерваторией Мауна-Лоа на Гавайях с 1980 по 2012 год [3].
Рис. 1-1, Среднемесячный CO2
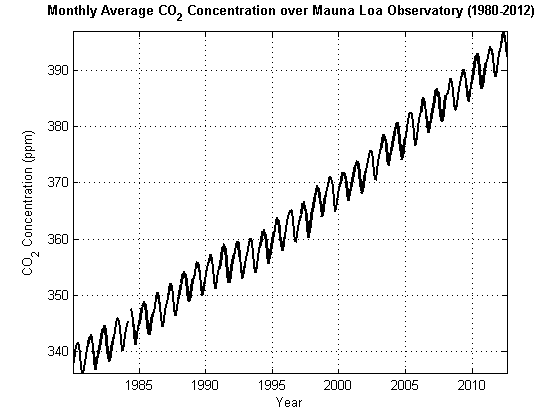
Стохастические процессы являются слабо стационарными или ковариационными стационарными (или просто стационарными), если их первые два момента являются конечными и постоянными с течением времени. В частности, если yt является стационарным стохастическим процессом, то для всех t:
E (yt) = λ < ∞.
V (yt) = start2 < ∞.
Cov (yt, yt-h) = γ h для всех лагов .
Кажется, что график вашего стохастического процесса увеличивается или уменьшается без привязки? Ответ на этот вопрос указывает, является ли стохастический процесс неподвижным. «Да» указывает, что стохастический процесс может быть нестационарным. На рис. 1-1, среднемесячная CO2, концентрация CO2 увеличивается без связывания, что указывает на нестационарный стохастический процесс.
Теорема Вольда [2] утверждает, что можно написать все слабо стационарные стохастические процессы в общем линейном виде
В данном случае обозначает последовательность некоррелированных (но не обязательно независимых) случайных величин из четко определенного распределения вероятностей со средним нулем. Его часто называют инновационным процессом, потому что он фиксирует всю новую информацию в системе в момент t.
Линейная модель временных рядов - это единичный корневой процесс, если решение, установленное для его характеристического уравнения, содержит корень, который находится на единичном круге (т.е. имеет абсолютное значение единицы). Впоследствии ожидаемое значение, дисперсия или ковариация элементов стохастического процесса растёт со временем, и поэтому является нестационарной. Если серия имеет корень единицы измерения, то разностный может сделать ее неподвижной.
Например, рассмотрим линейную модель временных рядов + αt, где αt - последовательность белого шума нововведений с дисперсией start2 (это называется случайной ходьбой). Характеристическое уравнение этой z − 1 = 0, имеющее корень единицы. Если начальное наблюдение y0 фиксировано, можно записать yt=y0+∑i=1tεi. Его ожидаемое значение - y0, что не зависит от времени. Тем не менее, дисперсия ряда составляет tstart2, которая растёт со временем делая ряд нестабильным. Возьмем первое различие для преобразования ряда и = yt − yt − 1 = αt. Характеристическое уравнение этого ряда равно z = 0, поэтому оно не имеет корня единицы измерения. Обратите внимание, что
0, что не зависит от времени,
start2, который не зависит от времени, и
) = 0, что не зависит от времени для всех целых чисел 0 < s < t.
Рис. 1-1, Среднемесячная CO2 не является статичной. Что произойдет, если построить график первой разности dt = yt-yt-1 этой серии? На рис. 1-2, «Ежемесячная разница в CO2» отображается dt. Игнорируя колебания, стохастический процесс, похоже, не увеличивается и не уменьшается в целом. Можно сделать вывод, что dt является неподвижным, а yt - единичным корнем нестационарным. Дополнительные сведения см. в разделе Дифференцирование.
Рис. 1-2, Ежемесячная разница в CO2
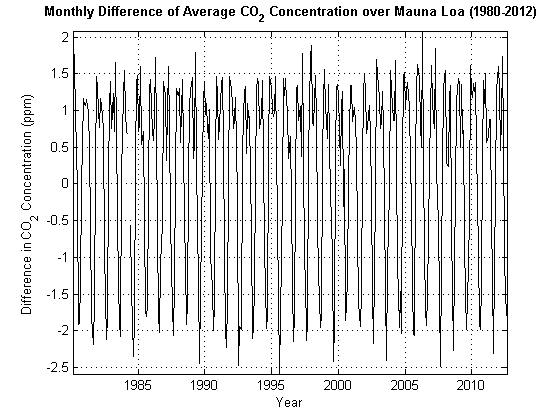
Оператор задержки L работает на временном ряду yt так, что Liyt = yt − i.
Многочлен запаздывания m-й степени коэффициентов b1, b2,..., bm определяется как
... + bmLm).
В нотации оператора запаздывания можно записать общую линейную модель, используя многочлен бесконечной степени (ψ2L2 +...),
αt.
Нельзя оценить модель, которая имеет многочлен бесконечной степени коэффициентов с конечным количеством данных. Однако, если (- рациональный многочлен (или приблизительно рациональный), можно записать его (по крайней мере, приблизительно) как частное двух многочленов конечной степени .
Определите q-градусный многочлен (+... + startqLq) и p-градусный Если (L) рациональен, то
L).
Таким образом, по теореме Волда можно моделировать (или близко аппроксимировать) каждый стационарный стохастический процесс как
t,
который имеет коэффициенты p + q (конечное число).
Степень p характерный полиномиал линейной модели временного ряда yt =ϕ1yt−1 +ϕ2yt−2
− 2 −... − δ p.
Это еще один способ оценить, что серия является стационарным процессом. Например, характеристическое уравнение 02yt = a2 − 0 .5a + 0,02.
Корни однородного характеристического уравнения (a) = 0 (характерными корнями) определяют, является ли линейный временной ряд неподвижным. Если каждый корень в (a) лежит единичной окружности, то процесс неподвижен. Корни лежат в пределах единичной окружности, если они имеют абсолютное значение меньше единицы. Это процесс корня единицы, если один или несколько корней лежат внутри круга единицы (т.е. имеют абсолютное значение единицы). Продолжая пример, характерные корни (a) = 0 {абсолютные значения этих корней меньше единицы, линейная модель временных рядов является стационарной.
[1] Бокс, Г. Э. П., Г. М. Дженкинс и Г. К. Рейнсель. Анализ временных рядов: прогнозирование и контроль. 3-й ред. Энглвуд Клиффс, Нью-Джерси: Прентис Холл, 1994.
[2] Wold, H. Исследование в анализе стационарных временных рядов. Уппсала, Швеция: Almqvist & Wiksell, 1938.
[3] Танс, П. и Р. Килинг. (2012, август). «Тенденции в области диоксида углерода в атмосфере». NOAA Research. Получено 5 октября 2012 г. из https://www.esrl.noaa.gov/gmd/ccgg/trends/mlo.html.