Определение условных средних моделей

Модель ARIMA по умолчанию

Модель ARIMA (p, D, q) по умолчанию в Econometrics Toolbox™ является несезонной моделью формы

$^{}_{ΔDyt} = c_{} +^{}_{} ϕ1ΔDyt -_{} 1^{} {+ +}_{}_{}_{} ΔpDyt -_{} p_{+}_{} δ 1αt$ − 1 +... + startqαt − q + αt.

Это уравнение можно записать в сжатом виде, используя нотацию оператора запаздывания:

$start(L {) (1}^{-}_{L}) Dyt =_{c}$ +

В любом уравнении распределение инноваций по умолчанию является гауссовым со средним нулем и постоянной дисперсией.

В командной строке можно указать модель этой формы с помощью краткого синтаксиса arima(p,D,q). Для входных аргументов p, D, и qвведите количество несезонных членов AR (p), порядок несезонного интегрирования (D) и количество несезонных членов MA (q) соответственно.

При использовании этого краткого синтаксиса arima создает arima с этими значениями свойств по умолчанию.

Имя свойства	Тип данных свойства
`AR`	Клеточный вектор `NaN`s
`Beta`	Пустой вектор `[]` коэффициентов регрессии, соответствующих экзогенным ковариатам
`Constant`	`NaN`
`D`	Степень несезонной интеграции, D
`Distribution`	`"Gaussian"`
`MA`	Клеточный вектор `NaN`s
`P`	Количество терминов AR плюс степень интеграции, p + D
`Q`	Количество терминов MA, q
`SAR`	Клеточный вектор `NaN`s
`SMA`	Клеточный вектор `NaN`s
`Variance`	`NaN`

Для назначения значений по умолчанию любым свойствам можно изменить созданный объект модели с помощью точечной нотации.

Обратите внимание, что входные данные D и q являются значениями arima присваивает свойствам D и Q. Однако входной аргумент p не обязательно является значением arima назначает свойству модели P. P сохраняет количество предварительных наблюдений, необходимых для инициализации компонента AR модели. Для несезонных моделей необходимое количество предварительных наблюдений равно p + D.

Для иллюстрации рассмотрим определение модели ARIMA (2,1,1)

$(1 -_{} {ϕ1L}_{} -^{} {ϕ2L2)}^{(} 1_{} - L)_{1yt} =_{c}$ + (1 + θ1L) αt,

где инновационный процесс является гауссовым с (неизвестной) постоянной дисперсией.

Mdl = arima(2,1,1)

Mdl = 
  arima with properties:

     Description: "ARIMA(2,1,1) Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 3
               D: 1
               Q: 1
        Constant: NaN
              AR: {NaN NaN} at lags [1 2]
             SAR: {}
              MA: {NaN} at lag [1]
             SMA: {}
     Seasonality: 0
            Beta: [1×0]
        Variance: NaN

Обратите внимание, что свойство модели P не имеет значения 2 (степень AR). С интеграцией для инициализации компонента AR модели необходимо всего p + D (здесь 2 + 1 = 3) предварительных наблюдений.

Созданная модель, Mdlимеет NaNs для всех параметров. A NaN значение сигнализирует, что параметр должен быть оценен или иным образом определен пользователем. Для прогнозирования или моделирования модели необходимо указать все параметры.

Чтобы оценить параметры, введите объект модели (вместе с данными) в estimate. Это возвращает новый подогнанный arima объект модели. Аппроксимированный объект модели имеет оценки параметров для каждого входа NaN значение.

Запрос arima без каких-либо входных аргументов возвращает спецификацию модели ARIMA (0,0,0) со значениями свойств по умолчанию:

DefaultMdl = arima

DefaultMdl = 
  arima with properties:

     Description: "ARIMA(0,0,0) Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 0
               D: 0
               Q: 0
        Constant: NaN
              AR: {}
             SAR: {}
              MA: {}
             SMA: {}
     Seasonality: 0
            Beta: [1×0]
        Variance: NaN

Задание несезонных моделей с использованием пар «имя-значение»

Лучший способ указать модели для arima использует аргументы пары имя-значение. Нет необходимости указывать значение для каждого свойства объекта модели. arima присваивает значения по умолчанию любым свойствам, которые не указаны (или не могут быть заданы).

В конденсированной нотации оператора запаздывания несезонные модели ARIMA (p, D, q) имеют вид

(L) {(1}^{-}_{L}) Dyt =_{c}

+ start( L) αt.

(1)

Эту модель можно расширить до модели ARIMAX (p, D, q) с линейным включением экзогенных переменных. Эта модель имеет форму

(L)_{}^{}_{}^{}^{} yt=c∗+xt′β+θ∗ (_{L})

αt,

(2)

где c^* = c/(1-L) D и θ* (L) = θ (L) / (1-L) D.

Совет

Если указано ненулевое значение D, то Econometrics Toolbox различает серию ответов _yt до того, как предикторы войдут в модель. Необходимо предварительно обработать экзогенные ковариаты xt путем тестирования на _{стационарность} и дифференциацию, если таковые являются нестатионными корневыми единицами. Если какой-либо нестационарный экзогенный ковариат входит в модель, то ложноотрицательная частота для тестов значимости β может увеличиться.

Для распределения нововведений, _αt, существует два варианта:

Независимый и идентично распределённый (iid) гауссов или Стьюдент т с постоянной дисперсией, $_{}^{startα2}$ .
Зависимый Gaussian или Student's t с процессом условной дисперсии2 $_{}^{}$ . Укажите модель условного отклонения с помощью garch, egarch, или gjr модель.

arima по умолчанию для инноваций используется iid гауссов процесс с постоянной (скалярной) дисперсией.

Для оценки, прогнозирования или моделирования модели необходимо указать параметрическую форму модели (например, какие задержки соответствуют ненулевым коэффициентам, распределение инноваций) и любые известные значения параметров. Можно задать любые неизвестные параметры, равные NaN, а затем введите модель в estimate (вместе с данными) для получения оценочных значений параметров.

arima (и estimate) возвращает модель, соответствующую спецификации модели. Можно изменить модели для изменения или обновления спецификации. Входные модели (без NaN значения) в forecast или simulate для прогнозирования и моделирования соответственно. Вот несколько примеров спецификаций, использующих аргументы «имя-значение».

Модель	Спецификация
$_{yt} = c_{} +_{} {δ 1yt}_{}$ − 1 + αt $_{αt} =_{}_{}$ startαzt _zt Гауссов	`arima('AR',NaN)` или `arima(1,0,0)`
$_{yt} =_{} {αt}_{} +_{} {start1αt}_{} -_{1}$ + start2αt − 2 $_{αt} =_{}_{}$ startαzt _zt Student's t с неизвестными степенями свободы	`arima('Constant',0,'MA',{NaN,NaN},... 'Distribution','t')`
$(1 − 0 . 8L) (1_{} - L) yt = 0,2_{+}$ (1 + 0 .6L) $_{δ t} =_{}$ 0,1 zt _zt Student's t с восемью степенями свободы	`arima('Constant',0.2,'AR',0.8,'MA',0.6,'D',1,... 'Variance',0.1^2,'Distribution',struct('Name','t','DoF',8))`
$(1 + 0 . {5L) (}^{1} -_{} L)_{}^{} \begin{matrix} 1Δyt \end{matrix} =_{xt}$ ′ [− 52] + αt $_{αt} ~ N ($ 0,1)	`arima('Constant',0,'AR',-0.5,'D',1,'Beta',[-5 2])`

Можно указать следующие аргументы «имя-значение» для создания несезонных arima модели.

Аргументы «имя-значение» для несезонных моделей ARIMA

Имя	Соответствующий модельный член (ы) в уравнении 1	Когда указывать
`AR`	Несезонные коэффициенты AR, $_{}_{}$	Установка ограничений равенства для коэффициентов AR. Например, чтобы задать коэффициенты AR в модели $_{yt} = 0_{.} 8yt − 1_{-} 0_{.}$ 2yt − 2 + αt, определить `'AR',{0.8,-0.2}`. Необходимо указать только ненулевые элементы `AR`. Если ненулевые коэффициенты имеют несоответствующие запаздывания, укажите соответствующие запаздывания с помощью `ARLags`. Любые указанные коэффициенты должны соответствовать стабильному многочлену оператора AR.
`ARLags`	Задержки, соответствующие ненулевым, несезонным коэффициентам AR	`ARLags` не является свойством модели. Использовать этот аргумент в качестве ярлыка для указания `AR` когда ненулевые коэффициенты AR соответствуют несектутивным запаздываниям. Например, чтобы задать ненулевые коэффициенты AR на лагах 1 и 12, например, $_{yt} =_{}_{}_{}_{}_{}$ `'ARLags',[1,12]`. Использовать `AR` и `ARLags` совместно для определения известных ненулевых коэффициентов AR при несектутивных лагах. Например, если в данной AR (12) модели ( $_{} 1) =$ 0,6 $_{и (} 12) =$ − 0,3, укажите`'AR',{0.6,-0.3},'ARLags',[1,12]`.
`Beta`	Значения коэффициентов экзогенных ковариат	Этот аргумент используется для указания значений коэффициентов экзогенных переменных. Например, использовать `'Beta',[0.5 7 -2]` для указания $β {= \begin{matrix} [ & 0,57 \end{matrix}}^{-}$ 2] ′. По умолчанию `Beta` является пустым вектором.
`Constant`	Постоянный член, c	Чтобы задать ограничения равенства для c. Например, для модели без постоянного члена укажите `'Constant',0`. По умолчанию `Constant` имеет значение `NaN`.
`D`	Степень несезонной дифференциации, D	Задание степени несезонной разностности больше нуля. Например, чтобы задать одну степень разностности, укажите `'D',1`. По умолчанию `D` имеет значение `0` (означает отсутствие несезонной интеграции).
`Distribution`	Распределение инновационного процесса	Используйте этот аргумент, чтобы указать распределение инноваций Student's. По умолчанию инновационное распределение - гауссово. Например, чтобы задать распределение t с неизвестными степенями свободы, укажите `'Distribution','t'`. Чтобы задать распределение инноваций с известными степенями свободы, назначьте `Distribution` структура данных с полями `Name` и `DoF`. Например, для распределения t с девятью степенями свободы укажите `'Distribution',struct('Name','t','DoF',9)`.
`MA`	Несезонные коэффициенты MA, $_{}_{}$	Установка ограничений равенства для коэффициентов МА. Например, чтобы задать коэффициенты MA в модели $_{yt} =_{} εt +_{0 .} 5xpt -_{1} +$ 0 .2αt − 2, определить `'MA',{0.5,0.2}`. Необходимо указать только ненулевые элементы `MA`. Если ненулевые коэффициенты имеют несоответствующие запаздывания, укажите соответствующие запаздывания с помощью `MALags`. Любые указанные коэффициенты должны соответствовать обратимому многочлену МА.
`MALags`	Задержки, соответствующие ненулевым, несезонным коэффициентам МА	`MALags` не является свойством модели. Использовать этот аргумент в качестве ярлыка для указания `MA` когда ненулевые коэффициенты МА соответствуют несектутивным запаздываниям. Например, чтобы задать ненулевые коэффициенты МА на лагах 1 и 4, например, $_{yt} =_{} {αt}_{} +_{} {start1αt}_{} -_{1} +$ start4αt − 4, определить `'MALags',[1,4]`. Использовать `MA` и `MALags` совместно для определения известных ненулевых коэффициентов МА при несектутивных лагах. Например, если в данной модели MA (4) $_{}$ $_{}$ `'MA',{0.4,0.2},'MALags',[1,4]`.
`Variance`	Скалярная дисперсия инновационного процесса, $_{}^{}$ Процесс условной дисперсии2 $_{}^{}$	Установить ограничения равенства для $_{}^{σε2}$ . Например, для модели с известной дисперсией 0.1 укажите `'Variance',0.1`. По умолчанию `Variance` имеет значение `NaN`. Чтобы задать модель условной дисперсии $_{}^{}$ , Набор `'Variance'` равно объекту модели условной дисперсии, например, `garch` объект модели.

Примечание

Невозможно назначить значения свойствам P и Q. Для несезонных моделей

arima наборы P равно p + D
arima наборы Q равно q

Задание мультипликативных моделей с использованием пар «имя-значение»

Какое-то время ряд с периодичностью s, определите _PS степени сезонный полиномиал оператора AR, $Φ (L) = (_{}^{_{}} {1−Φ1Lp1−}_{_{}}^{_{}}$ ...−ΦpsLps), и _{степень} qs сезонный $полиномиал$ оператора МА, Θ (L) = (1 +Θ1Lq1 +... + ΘqsLqs). Аналогично, определите $многочлен$ несезонного оператора AR степени p, (L) = (1 − ϕ1L −... − p Lp) и многочлен несезонного оператора степени q MA,

start(L) = (_{1} +_{θ1L}^{+} . .

. + startqLq).

(3)

Мультипликативная модель ARIMA со степенью D несезонной интеграции и степенью сезонности дана

Start(L) {(L) (}^{1} − L^{)} D_{} (1 - Ls) yt_{=}

c +

(4)

Серия инноваций может быть независимым или зависимым гауссовым или студенческим процессом. arima по умолчанию для распределения инноваций используется iid гауссов процесс с постоянной (скалярной) дисперсией.

В дополнение к аргументам для указания несезонных моделей (описанным в разделе Аргументы Name-Value для несезонных моделей ARIMA), можно указать эти аргументы name-value для создания мультипликативного arima модель. Модель ARIMAX можно расширить аналогичным образом, включив сезонные эффекты.

Аргументы «имя-значение» для сезонных моделей ARIMA

Аргумент	Соответствующий модельный член (ы) в уравнении 4	Когда указывать
`SAR`	Сезонные коэффициенты AR, $_{}_{_{}}$ Φ1,...,Φps	Установка ограничений равенства для сезонных коэффициентов AR. При задании коэффициентов AR используйте знак, противоположный тому, что появляется в уравнении 4 (то есть используйте знак коэффициента, как он появится в правой части уравнения). Использовать `SARLags` для указания лагов ненулевых сезонных коэффициентов AR. Укажите задержки, связанные с сезонными многочленами в периодичности наблюдаемых данных (например, 4, 8,... для квартальных данных, или 12, 24,... для ежемесячных данных), а не кратно сезонности (например, 1, 2,...). Например, для задания модели $(1 − 0 . 8L) (1^{−} 0_{.}_{} 2L12$ ) ыт = αт, определить `'AR',0.8,'SAR',0.2,'SARLags',12`. Любые введенные значения коэффициентов должны соответствовать стабильному сезонному многочлену AR.
`SARLags`	Задержки, соответствующие ненулевым сезонным коэффициентам AR, в периодичности наблюдаемых рядов	`SARLags` не является свойством модели. Использовать этот аргумент при указании `SAR` для указания лагов ненулевых сезонных коэффициентов AR. Например, для задания модели $(1 - δL) (_{1} -^{}_{} {Φ12L12}_{)}$ yt = αt, определить `'ARLags',1,'SARLags',12`.
`SMA`	Сезонные коэффициенты MA, $_{}_{_{}}$ Θ1,...,Θqs	Установка ограничений равенства для сезонных коэффициентов МА. Использовать `SMALags` для задания лагов ненулевых сезонных коэффициентов МА. Укажите задержки, связанные с сезонными многочленами в периодичности наблюдаемых данных (например, 4, 8,... для квартальных данных, или 12, 24,... для ежемесячных данных), а не кратно сезонности (например, 1, 2,...). Например, для задания модели $_{yt} = (1 + 0 . 6L) (^{1} +_{0}$ .2L12) αt, определить `'MA',0.6,'SMA',0.2,'SMALags',12`. Любые введенные значения коэффициентов должны соответствовать обратимому сезонному многочлену МА.
`SMALags`	Задержки, соответствующие ненулевым сезонным коэффициентам МА, в периодичности наблюдаемых рядов	`SMALags` не является свойством модели. Использовать этот аргумент при указании `SMA` для указания лагов ненулевых сезонных коэффициентов МА. Например, для задания модели $_{yt} = (1_{} + θ1L)_{} (^{1} +_{}$ Θ4L4) αt, определить `'MALags',1,'SMALags',4`.
`Seasonality`	Сезонная периодичность, с	Чтобы задать степень сезонного интегрирования s в сезонном разностном многочлене _Δs = 1 - ^Ls. Например, для определения периодичности сезонной интеграции ежемесячных данных укажите `'Seasonality',12`. Если указано ненулевое значение `Seasonality`, то степень всего сезонного разностного полинома равна единице. По умолчанию `Seasonality` имеет значение `0` (означает периодичность и отсутствие сезонной интеграции).

Примечание

Невозможно назначить значения свойствам P и Q. Для мультипликативных моделей ARIMA,

arima наборы P равно p + D + _ps + s
arima наборы Q равно q + _qs

Укажите условную среднюю модель с помощью приложения эконометрического моделирования

Вы можете указать структуру запаздывания и распределение инноваций сезонных и несезонных условных средних моделей с помощью приложения Econometric Modeler. Приложение рассматривает все коэффициенты как неизвестные и оцениваемые, включая параметр степеней свободы для распределения инноваций.

В командной строке откройте приложение Econometric Modeler.

econometricModeler

Можно также открыть приложение из галереи приложений (см. Econometric Modeler).

В приложении можно просмотреть все поддерживаемые модели, выбрав переменную временного ряда для ответа на панели Временной ряд. Затем на вкладке Эконометрический моделирующий (Econometric Modeler) в разделе Модели (Models) щелкните стрелку, чтобы отобразить галерею моделей.

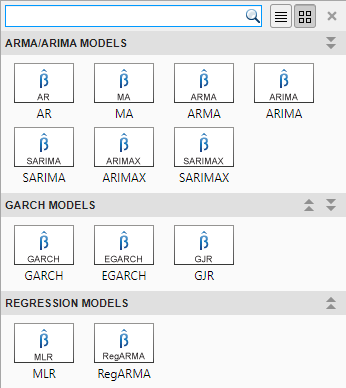
Раздел ARMA/ARIMA Models содержит поддерживаемые модели условного среднего.

Для оценки условных средних моделей SARIMA и SARIMAX являются наиболее гибкими моделями. Можно создать любую модель условного среднего, которая исключает экзогенные предикторы, нажав SARIMA, или любую модель условного среднего, которая включает хотя бы один экзогенный предиктор, нажав SARIMAX.

После выбора модели приложение отображает Type диалоговое окно «Параметры модели», где Type - тип модели. На этом рисунке показано диалоговое окно «Параметры модели SARIMAX».

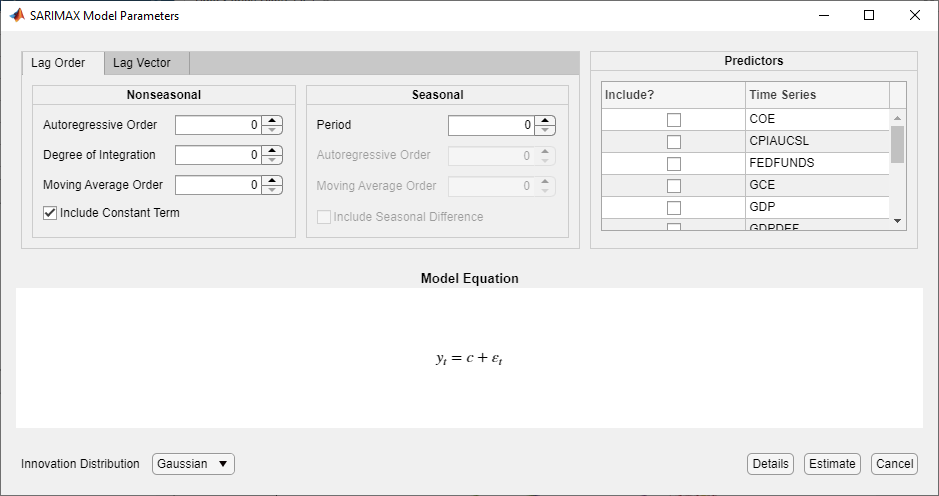
Регулируемые параметры в диалоговом окне зависят от Type. В целом, регулируемые параметры включают в себя:

Константа модели и коэффициенты линейной регрессии, соответствующие переменным предиктора
Параметры компонентов временных рядов, которые включают сезонные и несезонные задержки и степени интеграции
Распределение инноваций

При корректировке значений параметров уравнение в разделе «Уравнение модели» изменяется в соответствии со спецификациями. Регулируемые параметры соответствуют аргументам пары «вход» и «имя-значение», описанным в предыдущих разделах и в arima справочная страница.

Дополнительные сведения об указании моделей с помощью приложения см. в разделах Подгонка моделей к данным и Определение многочленов оператора задержки в интерактивном режиме.

Документация