Определение моделей GJR

Модель GJR по умолчанию

Модель GJR (P, Q) по умолчанию в Econometrics Toolbox™ имеет вид

$_{αt} =_{}_{}$ starttzt,

с гауссовым распространением инноваций и

$_{}^{}_{}^{}_{}_{}^{}_{}^{}_{}_{}^{}_{}^{}_{}_{}_{}^{σt2=κ+∑i=1Pγiσt−i2+∑j=1Qαjεt−j2+∑j=1QξjI[εt−j<0]εt−j2} .$

Индикаторная функция $I [_{αt} - j$ < 0] равна ${1,}_{если}$ αt − j < 0 и 0 в противном случае. Модель по умолчанию не имеет среднего смещения, а запаздывающие отклонения и квадратичные нововведения имеют последовательные задержки.

Можно указать модель этой формы с помощью краткого синтаксиса gjr(P,Q). Для входных аргументов P и Qвведите количество запаздывающих отклонений (члены GARCH), P и запаздывающих квадратичных инноваций (ARCH и члены левериджа), Q соответственно. Действуют следующие ограничения:

P и Q должны быть неотрицательными целыми числами.
Если P > 0, то необходимо также указать Q > 0

При использовании этого краткого синтаксиса gjr создает gjr с этими значениями свойств по умолчанию.

Собственность	Значение по умолчанию
`P`	Количество терминов GARCH, P
`Q`	Количество условий ARCH и рычагов, Q
`Offset`	`0`
`Constant`	`NaN`
`GARCH`	Клеточный вектор `NaN`s
`ARCH`	Клеточный вектор `NaN`s
`Leverage`	Клеточный вектор `NaN`s
`Distribution`	`"Gaussian"`

Чтобы назначить значения по умолчанию любым свойствам, можно изменить созданную модель с помощью точечной нотации.

Для иллюстрации рассмотрите возможность задания модели GJR (1,1)

$_{αt} =_{}_{}$ starttzt,

с гауссовым распространением инноваций и

$_{}^{startt2} = {start+}_{}_{}^{} γ 1startt_{−}_{12}^{+}_{} α1αt_{-} 12 +_{ξ1I}^{} [$ αt − 1 < 0] αt − 12.

Mdl = gjr(1,1)

Mdl = 
  gjr with properties:

     Description: "GJR(1,1) Conditional Variance Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 1
               Q: 1
        Constant: NaN
           GARCH: {NaN} at lag [1]
            ARCH: {NaN} at lag [1]
        Leverage: {NaN} at lag [1]
          Offset: 0

Созданная модель, Mdlимеет NaNs для всех параметров модели. A NaN значение сигнализирует, что параметр должен быть оценен или иным образом определен пользователем. Для прогнозирования или моделирования модели необходимо указать все параметры.

Для оценки параметров введите модель (вместе с данными) в estimate. Это возвращает новый подогнанный gjr модель. Подогнанная модель имеет оценки параметров для каждого входа NaN значение.

Запрос gjr без каких-либо входных аргументов возвращает спецификацию модели GJR (0,0) со значениями свойств по умолчанию:

DefaultMdl = gjr

DefaultMdl = 
  gjr with properties:

     Description: "GJR(0,0) Conditional Variance Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 0
               Q: 0
        Constant: NaN
           GARCH: {}
            ARCH: {}
        Leverage: {}
          Offset: 0

Задание модели GJR по умолчанию

Открыть сценарий в реальном времени

В этом примере показано использование краткого текста gjr(P,Q) синтаксис, определяющий модель GJR (P, Q) по умолчанию, $_{}_{}_{}$

$_{}^{}_{}^{}_{}_{}^{}_{}^{}_{}_{}^{}_{}^{}_{}_{}_{}^{σt2=κ+∑i=1Pγiσt-i2+∑j=1Qαjεt-j2+∑j=1QξjI[εt-j<0]εt-j2} .$

По умолчанию все параметры в созданной модели имеют неизвестные значения.

Укажите модель GJR (1,1) по умолчанию :

Mdl = gjr(1,1)

Mdl = 
  gjr with properties:

     Description: "GJR(1,1) Conditional Variance Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 1
               Q: 1
        Constant: NaN
           GARCH: {NaN} at lag [1]
            ARCH: {NaN} at lag [1]
        Leverage: {NaN} at lag [1]
          Offset: 0

Выходные данные показывают, что созданная модель, Mdlимеет NaN значения для всех параметров модели: постоянный член, коэффициент GARCH, коэффициент ARCH и коэффициент левериджа. Можно изменить созданную модель с помощью точечной нотации или ввести ее (вместе с данными) в estimate.

Использование аргументов пары «имя-значение»

Наиболее гибким способом определения моделей GJR является использование аргументов пары имя-значение. Нет необходимости указывать значение для каждого свойства модели. gjr присваивает значения по умолчанию любым свойствам модели, которые не указаны (или не могут быть заданы).

Общая модель GJR (P, Q) имеет вид

$_{yt} = λ_{} +$ αt,

, где $_{αt} =_{}_{}$ starttzt и

$_{}^{}_{}^{}_{}_{}^{}_{}^{}_{}_{}^{}_{}^{}_{}_{}_{}^{σt2=κ+∑i=1Pγiσt−i2+∑j=1Qαjεt−j2+∑j=1QξjI[εt−j<0]εt−j2} .$

Инновационное распределение может быть гауссовым или студенческим.

Для оценки, прогнозирования или моделирования модели необходимо указать параметрическую форму модели (например, какие задержки соответствуют ненулевым коэффициентам, распределение инноваций) и любые известные значения параметров. Можно задать любые неизвестные параметры, равные NaN, а затем введите модель в estimate (вместе с данными) для получения оценочных значений параметров.

gjr (и estimate) возвращает модель, соответствующую спецификации модели. Можно изменить модели для изменения или обновления спецификации. Входные модели (без NaN значения) в forecast или simulate для прогнозирования и моделирования соответственно. Вот несколько примеров спецификаций, использующих аргументы «имя-значение».

Модель	Спецификация
$_{yt} =_{}$ αt $_{αt} =_{}_{}$ starttzt _zt Гауссов $_{}^{startt2} = {start+}_{}_{}^{} γ 1startt_{−}_{12}^{+}_{} α1αt_{-} 12 +_{ξ1I}^{}$ [αt − 1 < 0] αt − 12	`gjr('GARCH',NaN,'ARCH',NaN,... 'Leverage',NaN)` или `gjr(1,1)`
$_{yt} =_{}$ $_{αt} =_{}_{}$ starttzt _zt Student's t с неизвестными степенями свободы $_{}^{startt2} = {start+}_{}_{}^{} γ 1startt_{−}_{12}^{+}_{} α1αt_{-} 12 +_{ξ1I}^{}$ [αt − 1 < 0] αt − 12	`gjr('Offset',NaN,'GARCH',NaN,... 'ARCH',NaN,'Leverage',NaN,... 'Distribution','t')`
$_{yt} =_{}$ αt $_{αt} =_{}_{}$ starttzt _zt Student's t с восемью степенями свободы $_{}^{startt2} = 0,1 +_{}^{} 0,6startt −_{12 +}^{} 0,3αt -_{12} +_{0,05I}^{}$ [αt − 1 < 0] αt − 12	`gjr('Constant',0.1,'GARCH',0.6,... 'ARCH',0.3,'Leverage',0.05,... 'Distribution',... struct('Name','t','DoF',8))`

Ниже приведено полное описание аргументов «имя-значение», которые можно использовать для указания моделей GJR.

Примечание

Невозможно назначить значения свойствам P и Q. egarch наборы P равно наибольшему запаздыванию GARCH, и Q равен наибольшему запаздыванию с ненулевым квадратом инновационного коэффициента, включая ARCH и коэффициенты левериджа.

Аргументы «имя-значение» для моделей GJR

Имя	Соответствующие термины модели GJR	Когда указывать
`Offset`	Среднее смещение, λ	Включение ненулевого среднего смещения. Например, `'Offset',0.2`. Если планируется оценить условие смещения, укажите `'Offset',NaN`. По умолчанию `Offset` имеет значение `0` (означает, без смещения).
`Constant`	Константа в модели условной дисперсии,	Установить ограничения равенства для κ. Например, если для модели известна константа 0.1, укажите `'Constant',0.1`. По умолчанию `Constant` имеет значение `NaN`.
`GARCH`	Коэффициенты GARCH, $_{}_{}$ γ1,...,γP	Установка ограничений равенства для коэффициентов GARCH. Например, чтобы задать модель GJR (1,1) с $_{} γ 1 =$ 0,6, укажите`'GARCH',0.6`. Необходимо указать только ненулевые элементы `GARCH`. Если ненулевые коэффициенты имеют несоответствующие запаздывания, укажите соответствующие запаздывания с помощью `GARCHLags`. Любые указанные коэффициенты должны удовлетворять всем ограничениям стационарности.
`GARCHLags`	Задержки, соответствующие ненулевым коэффициентам GARCH	`GARCHLags` не является свойством модели. Использовать этот аргумент в качестве ярлыка для указания `GARCH` когда ненулевые коэффициенты GARCH соответствуют несектутивным запаздываниям. Например, чтобы задать ненулевые коэффициенты GARCH на лагах 1 и 3, например ненулевые $_{γ 1}$ и $_{γ 3},$ укажите `'GARCHLags',[1,3]`. Использовать `GARCH` и `GARCHLags` совместно для определения известных ненулевых коэффициентов GARCH при несектутивных лагах. Например, если $_{γ 1} =$ 0,3 $и_{} γ 3 =$ 0,1, укажите`'GARCH',{0.3,0.1},'GARCHLags',[1,3]`
`ARCH`	Коэффициенты ARCH, $_{}_{}$ α1,...,αQ	Установка ограничений равенства для коэффициентов ARCH. Например, чтобы задать модель GJR (1,1) с $_{} α1 =$ 0,3, укажите`'ARCH',0.3`. Необходимо указать только ненулевые элементы `ARCH`. Если ненулевые коэффициенты имеют несоответствующие запаздывания, укажите соответствующие запаздывания с помощью `ARCHLags`.
`ARCHLags`	Задержки, соответствующие ненулевым коэффициентам ARCH	`ARCHLags` не является свойством модели. Использовать этот аргумент в качестве ярлыка для указания `ARCH` когда ненулевые коэффициенты ARCH соответствуют несектутивным запаздываниям. Например, чтобы задать ненулевые коэффициенты ARCH на лагах 1 и 3, например ненулевые $_{α1}$ и $_{α3},$ укажите `'ARCHLags',[1,3]`. Использовать `ARCH` и `ARCHLags` совместно для задания известных ненулевых коэффициентов ARCH при несектутивных лагах. Например, если $_{α1} =$ 0,4 $и_{} α3 =$ 0,2, укажите`'ARCH',{0.4,0.2},'ARCHLags',[1,3]`
`Leverage`	Коэффициенты левериджа, $_{}_{}$ ξ1,...,ξQ	Установка ограничений равенства для коэффициентов левериджа. Например, чтобы задать модель GJR (1,1), где $_{}$ `'Leverage',0.1`. Необходимо указать только ненулевые элементы `Leverage`. Если ненулевые коэффициенты имеют несоответствующие запаздывания, укажите соответствующие запаздывания с помощью `LeverageLags`.
`LeverageLags`	Задержки, соответствующие ненулевым коэффициентам левериджа	`LeverageLags` не является свойством модели. Использовать этот аргумент в качестве ярлыка для указания `Leverage` когда ненулевые коэффициенты левериджа соответствуют несектутивным запаздываниям. Например, чтобы задать ненулевые коэффициенты левериджа на лагах 1 и 3, например, ненулевые $_{}$ $_{}$ `'LeverageLags',[1,3]`. Использовать `Leverage` и `LeverageLags` вместе для определения известных ненулевых коэффициентов левериджа при несектутивных лагах. Например, если $_{«» «» «» «» «» «» «» «» «» «»}$ $_{}$ «» «» «» «» «» «» «»`'Leverage',{0.1,0.05},'LeverageLags',[1,3]`.
`Distribution`	Распределение инновационного процесса	Используйте этот аргумент, чтобы указать распределение инноваций Student's. По умолчанию инновационное распределение - гауссово. Например, чтобы задать распределение t с неизвестными степенями свободы, укажите `'Distribution','t'`. Чтобы задать распределение инноваций с известными степенями свободы, назначьте `Distribution` структура данных с полями `Name` и `DoF`. Например, для распределения t с девятью степенями свободы укажите `'Distribution',struct('Name','t','DoF',9)`.

Задание модели GJR с помощью приложения Econometric Modeler

Вы можете указать структуру запаздывания, распределение инноваций и преимущества моделей GJR с помощью приложения Econometric Modeler. Приложение рассматривает все коэффициенты как неизвестные и оцениваемые, включая параметр степеней свободы для распределения инноваций.

В командной строке откройте приложение Econometric Modeler.

econometricModeler

Можно также открыть приложение из галереи приложений (см. Econometric Modeler).

В приложении можно просмотреть все поддерживаемые модели, выбрав переменную временного ряда для ответа на панели Временной ряд. Затем на вкладке Эконометрический моделирующий (Econometric Modeler) в разделе Модели (Models) щелкните стрелку, чтобы отобразить галерею моделей.

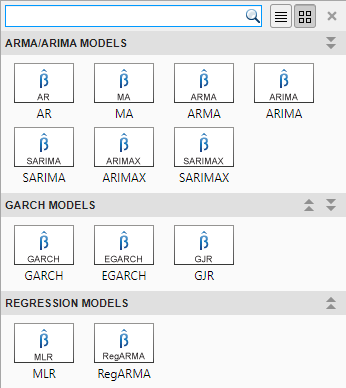
Раздел GARCH Models содержит все поддерживаемые модели условных отклонений. Чтобы указать модель GJR, щелкните GJR. Откроется диалоговое окно Параметры модели GJR (GJR Model Parameters).

К регулируемым параметрам относятся:

Степень GARCH - порядок многочлена GARCH.
Степень ARCH - порядок многочлена ARCH. Значение этого параметра также определяет порядок многочлена рычага.
Включить смещение (Include Offset) - включение смещения модели.
Распространение инноваций - распространение инноваций.

При корректировке значений параметров уравнение в разделе «Уравнение модели» изменяется в соответствии со спецификациями. Регулируемые параметры соответствуют аргументам пары «вход» и «имя-значение», описанным в предыдущих разделах и в gjr справочная страница.

Дополнительные сведения об указании моделей с помощью приложения см. в разделах Подгонка моделей к данным и Определение многочленов оператора задержки в интерактивном режиме.

Задание модели GJR со средним смещением

Открыть сценарий в реальном времени

В этом примере показано, как задать модель GJR (P, Q) со средним смещением. Используйте аргументы пары имя-значение, чтобы указать модель, которая отличается от модели по умолчанию .

Укажите модель GJR (1,1) со средним смещением ,

$_{yt} = λ_{} +$ αt,

, где $_{αt} =_{}_{}$ starttzt и

$_{}^{startt2} = {start+}_{}_{}^{}_{} {γ 1startt-12}_{+}^{}_{} {α1αt-12}_{+} ξ1I_{[}^{} αt-1$ < 0] αt-12.

Mdl = gjr('Offset',NaN,'GARCHLags',1,'ARCHLags',1,...
    'LeverageLags',1)

Mdl = 
  gjr with properties:

     Description: "GJR(1,1) Conditional Variance Model with Offset (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 1
               Q: 1
        Constant: NaN
           GARCH: {NaN} at lag [1]
            ARCH: {NaN} at lag [1]
        Leverage: {NaN} at lag [1]
          Offset: NaN

Среднее смещение отображается на выходе как дополнительный параметр, который должен быть оценен или указан иным образом.

Укажите модель GJR с несектутивными лагами

Открыть сценарий в реальном времени

В этом примере показано, как указать модель GJR с ненулевыми коэффициентами при несектутивных лагах.

Укажите модель GJR (3,1) с ненулевыми членами GARCH на лагах 1 и 3. Включить среднее смещение .

Mdl = gjr('Offset',NaN,'GARCHLags',[1,3],'ARCHLags',1,...
    'LeverageLags',1)

Mdl = 
  gjr with properties:

     Description: "GJR(3,1) Conditional Variance Model with Offset (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 3
               Q: 1
        Constant: NaN
           GARCH: {NaN NaN} at lags [1 3]
            ARCH: {NaN} at lag [1]
        Leverage: {NaN} at lag [1]
          Offset: NaN

Неизвестные ненулевые коэффициенты GARCH соответствуют запаздывающим дисперсиям на лагах 1 и 3. Выходные данные показывают только ненулевые коэффициенты.

Отображение значения GARCH:

Mdl.GARCH

ans=1×3 cell array
    {[NaN]}    {[0]}    {[NaN]}

GARCH массив ячеек возвращает три элемента. Первый и третий элементы имеют значение NaN, указывая, что эти коэффициенты ненулевые и должны быть оценены или указаны иным образом. По умолчанию gjr устанавливает промежуточный коэффициент с запаздыванием 2 равным нулю для поддержания согласованности с индексацией массива ячеек MATLAB ® .

Задание модели GJR с известными значениями параметров

Открыть сценарий в реальном времени

В этом примере показано, как указать модель GJR с известными значениями параметров. Такую полностью заданную модель можно использовать в качестве входных данных для simulate или forecast.

Укажите модель GJR (1,1)

$_{}^{startt2} = 0,1 +_{}^{} 0,6startt-12_{+}^{} 0,2αt-12_{+} 0,1I_{[}^{}$ αt-1 < 0] αt-12

с гауссовым инновационным распределением.

Mdl = gjr('Constant',0.1,'GARCH',0.6,'ARCH',0.2,...
    'Leverage',0.1)

Mdl = 
  gjr with properties:

     Description: "GJR(1,1) Conditional Variance Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 1
               Q: 1
        Constant: 0.1
           GARCH: {0.6} at lag [1]
            ARCH: {0.2} at lag [1]
        Leverage: {0.1} at lag [1]
          Offset: 0

Поскольку указаны все значения параметров, созданная модель не имеет NaN значения. Функции simulate и forecast не принимать входные модели с NaN значения.

Определение модели GJR с распределением инноваций

Открыть сценарий в реальном времени

В этом примере показано, как указать модель GJR с распределением инноваций Student's.

Укажите модель GJR (1,1) со средним смещением ,

$_{yt} = λ_{} +$ αt,

, где $_{αt} =_{}_{}$ starttzt и

$_{}^{startt2} = {start+}_{}_{}^{}_{} {γ 1startt-12}_{+}^{}_{} {α1αt-12}_{+} ξ1I_{[}^{} αt-1$ < 0] αt-12.

Предположим, $_{что zt}$ следует распределению инноваций Student с 10 степенями свободы.

tDist = struct('Name','t','DoF',10);
Mdl = gjr('Offset',NaN,'GARCHLags',1,'ARCHLags',1,...
              'LeverageLags',1,'Distribution',tDist)

Mdl = 
  gjr with properties:

     Description: "GJR(1,1) Conditional Variance Model with Offset (t Distribution)"
    Distribution: Name = "t", DoF = 10
               P: 1
               Q: 1
        Constant: NaN
           GARCH: {NaN} at lag [1]
            ARCH: {NaN} at lag [1]
        Leverage: {NaN} at lag [1]
          Offset: NaN

Значение Distribution является struct массив с полем Name равно 't' и на местах DoF равно 10. При указании степеней свободы они не оцениваются при вводе модели в estimate.

Документация