Документация

Предвзятые оценки

Если выборки игнорируются, количество выборок, используемых при оценке, меньше, чем NumSamples. Очевидно, что фактическое количество использованных образцов должно быть достаточным для получения оценок. Кроме того, хотя параметры модели Parameters (или средние оценки Mean) - несмещенные оценки максимального правдоподобия, оценка остаточной ковариации Covariance является предвзятым. Чтобы преобразовать в несмещенную оценку ковариации, умножьте Covariance около

где Count - фактическое количество выборок, использованных при оценке Count ≤ NumSamples. Ни одна из функций регрессии не выполняет эту корректировку.

Требования

Функции регрессии, в частности функции оценки, имеют несколько требований. Во-первых, они должны иметь согласованные значения для NumSamples, NumSeries, и NumParams. Как правило, многомерные функции нормальной регрессии требуют

а функции регрессии методом наименьших квадратов требуют

где Count - фактическое количество выборок, использованных при оценке

Во-вторых, они должны иметь достаточно непутевых значений, чтобы сойтись. В-третьих, они должны иметь недегенеративную ковариационную матрицу.

Хотя в ссылках можно найти некоторые необходимые и достаточные условия, общих условий существования и уникальности решений в случае отсутствия данных не существует. Несогласованность обычно происходит из-за плохо обусловленной оценки ковариационной матрицы, которая более подробно обсуждается в Nonconvergence.

Медленная сходимость

Поскольку в худшем случае сходимость алгоритма ЕСМ является линейной, перед завершением алгоритма можно выполнить сотни и даже тысячи итераций. Если вы регулярно оцениваете алгоритм ECM с регулярными обновлениями, вы можете использовать предыдущие оценки в качестве начальных предположений для оценки следующего периода. Этот подход часто ускоряет процесс, поскольку инициализация по умолчанию в функциях регрессии устанавливает начальные параметры. b до нуля и начальной ковариации C быть единичной матрицей.

Возможны и другие импровизированные подходы, хотя большинство подходов зависят от проблем. В частности, для средней и ковариационной оценки функция оценки ecmnmle использует функцию ecmninit для получения первоначальной оценки.

Нерандомские остатки

Одновременные оценки параметров b и ковариации C потребовать C быть позитивно-определенным. Таким образом, общие процедуры многомерной нормальной регрессии требуют недегенеративных остаточных ошибок. Если вы столкнулись с моделью, которая имеет точные результаты, процедура наименьших квадратов ecmlsrmle всё ещё работает, хотя и предоставляет оценку наименьших квадратов с сингулярной матрицей остаточной ковариации. Другие функции регрессии не выполняются.

Несходимость

Хотя функции регрессии надежны и работают для большинства «типичных» случаев, они могут не сходиться. Основным режимом отказа является плохо обусловленная ковариационная матрица, где отказы являются либо мягкими, либо жесткими. Мягкий сбой бесконечно блуждает к почти сингулярной ковариационной матрице и может быть замечен, если алгоритм не сходится примерно после 100 итераций. Если MaxIterations увеличивается до 500 и инициируется режим отображения (без выходных аргументов), типичный мягкий сбой выглядит так.

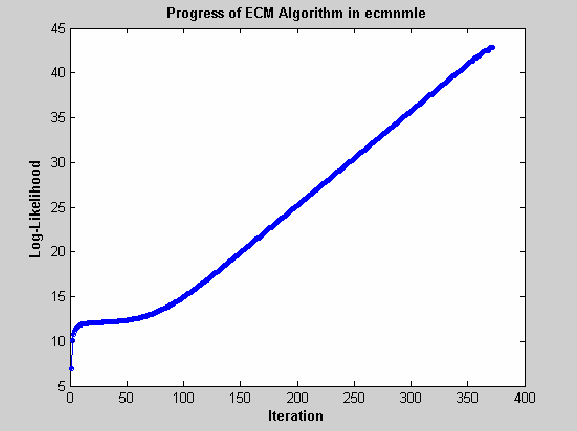
Этот случай, который основан на 20 наблюдениях пяти активов с 30% отсутствующих данных, показывает, что логарифмическое правдоподобие проходит линейно до бесконечности, когда функция правдоподобия переходит к 0. В этом случае функция сходится, но ковариационная матрица фактически сингулярна с наименьшим собственным значением в порядке точности машины (eps).

Для функции ecmnmle, жесткая ошибка выглядит следующим образом:

> In ecmninit at 60
  In ecmnmle at 140
??? Error using ==> ecmnmle
Full covariance not positive-definite in iteration 218.

С практической точки зрения, если есть сомнения, проверьте вашу остаточную ковариационную матрицу из процедур регрессии, чтобы убедиться, что она является положительной-определенной. Это важно, потому что мягкая ошибка имеет матрицу, которая кажется положительной-определенной, но на самом деле имеет близкое к нулю собственное значение в пределах точности машины. Для этого используется оценка ковариации Covariance, использовать cond(Covariance), где любое значение больше, чем 1/eps должен считаться подозреваемым.

Однако, если происходит сбой любого типа, обратите внимание на то, что процедура регрессии указывает на то, что с данными, вероятно, что-то не так. (Даже при отсутствии пропущенных данных два временных ряда, которые пропорциональны друг другу, образуют сингулярную ковариационную матрицу.)