Сведения об определенных линейных моделях

Что такое модели IDLTI?

Программное обеспечение System Identification Toolbox™ использует объекты для представления различных линейных и нелинейных структур модели. Эти объекты линейной модели в совокупности известны как модели IDLTI (IDentified Linear Time-Invariant).

Модели IDLTI содержат два различных динамических компонента:

Измеряемый компонент - описывает взаимосвязь между измеряемыми входами и измеряемым выходом (G)
Компонент шума - описывает взаимосвязь между возмущениями на выходе и измеренным выходом (H)

Модели, имеющие только шумовую составляющую H называются моделями временных рядов или сигналов. Как правило, такие модели создаются с использованием данных временных рядов, состоящих из одного или нескольких выходных данных. y(t) без соответствующего ввода.

Общий выходной сигнал представляет собой сумму вкладов измеренных входов и возмущений: y = G u + H e, где u представляет измеренные входы и e возмущение. e (t) моделируется как нулевой средний гауссовский белый шум с дисперсией Λ. На следующем рисунке показана модель IDLTI.

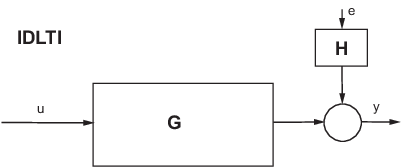
При моделировании модели IDLTI изучается влияние входных данных u (t) (и, возможно, начальных условий) на выходные данные y (t). Шум e (t) не учитывается. Однако при прогнозировании выходного сигнала с конечным горизонтом как измеренная, так и шумовая составляющие модели способствуют вычислению (предсказанного) отклика.

Модель прогнозирования на один шаг вперед, соответствующая линейной идентифицированной модели (y = Gu + He)

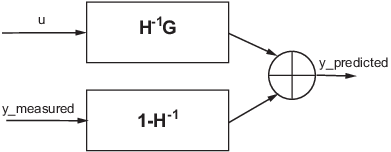
Параметризация измеренных и шумовых компонентов

Различные структуры линейной модели обеспечивают различные способы параметризации передаточных функций. G и H. При построении модели IDLTI или оценке модели непосредственно с использованием данных ввода-вывода можно сконфигурировать структуру как G, так и H, как описано в следующей таблице:

Тип модели	Передаточные функции G и H	Метод конфигурирования
Модель пространства состояния (`idss`)	Представляет идентифицированную структуру модели состояния-пространства, определяемую уравнениями: $\begin{array}{l} \overset{}{} \\ x˙=Ax+Bu+Key=Cx+Du+e \end{array}$ где передаточная функция между измеренным входом u и выходом y равна $G (s) {= C (}^{sI} - A$ ) − 1B + D, а передаточная $функция$ шума равна H (s) = C (sI − A) − 1K + I.	Конструкция: Использование `idss` для создания модели с заданием значений матриц состояния-пространства A, B, C, D и K в качестве входных аргументов (с использованием `NaNs` для обозначения неизвестных записей). Оценка: Использование `ssest` или `n4sid`, определение пар имя-значение для различных конфигураций, таких как каноническая параметризация измеряемой динамики (`'Form'/'canonical'`), обозначающего отсутствие сквозного прохода фиксацией D к нулю (`'Feedthrough'/false`) и отсутствие шумовой динамики фиксацией К к нулю (`'DisturbanceModel'/'none'`).
Полиномиальная модель (`idpoly`)	Представляет полиномиальную модель, такую как ARX, ARMAX и BJ. Модель ARMAX, например, использует уравнение «вход-выход» Ay (t) = Bu (t) + Ce (t), так что измеренная передаточная функция $G равна G^{(} s$ ) = A − 1B, тогда как $функция$ передачи шума равна H (s) = A − 1C. Модель ARMAX представляет собой специальную конфигурацию общей полиномиальной модели, управляющим уравнением которой является: $Ay (t) \frac{}{=} BFu \frac{(}{t}) +$ CDe (t) Авторегрессионная составляющая А является общей для измеряемой составляющей и составляющей шума. Многочлены B и F составляют измеренную составляющую, в то время как многочлены C и D составляют шумовую составляющую.	Конструкция: Использование `idpoly` для создания модели с использованием значений активных многочленов в качестве входных аргументов. Например, для создания модели «Output-Error», использующей `G = B/F` в качестве измеряемой составляющей и имеет тривиальную шумовую составляющую (`H = 1`). введите: y = idpoly([],B,[],[],F) Оценка: Использовать `armax`, `arx`, или `bj`, указывая порядки многочленов в качестве входных аргументов. Например, `bj` требуется задать порядки многочленов B, C, D и F для построения модели с управляющим уравнением $y (t) \frac{}{=} BFu \frac{(}{t}) +$ CDe (t)
Модель передаточной функции (`idtf`)	Представляет идентифицированную модель передаточной функции, которая не имеет динамических элементов для моделирования шумового поведения. Этот объект использует тривиальную модель шума H (s) = I. Управляющее уравнение $y (t) \frac{=}{} numdenu (t)$ + e (t)	Конструкция: Использование `idtf` создание модели с заданием значений числителя и коэффициентов знаменателя в качестве входных аргументов. Векторы числителя и знаменателя составляют измеряемую составляющую `G = num(s)/den(s)`. Компонент шума фиксируется на `H = 1`. Оценка: Использование `tfest`, указание количества полюсов и нулей измеряемого компонента `G`.
Модель процесса (`idproc`)	Представляет модель процесса, которая предоставляет опции для представления динамики шума как ARMA-процесса первого или второго порядка (то есть H (s) = C (s )/A (s), где C (s) и A (s) являются моническими многочленами равной степени). Измеренный компонент G (s) представлен передаточной функцией, выраженной в виде полюса-нуля.	Для моделей процессов (и «серый ящик») компонент шума часто рассматривается как расширение по требованию к измеренному в противном случае представлению, ориентированному на компоненты. Для этих моделей можно добавить компонент шума с помощью `DisturbanceModel` вариант оценки. Например: model = procest(data,'P1D') оценивает модель, уравнение которой: $y (s)_{=} \frac{}{_{Kp1} (} {Tp1s}^{+ 1}) e - sTdu$ (s) + e (s). Чтобы добавить в модель компонент шума второго порядка, используйте: Options = procestOptions('DisturbanceModel','ARMA1'); model = procest(data,'P1D',Options); Эта модель имеет уравнение: $y (s)_{=} \frac{}{_{Kp1} (} {Tp1s}^{+ 1}) e - \frac{_{} sTdu}{(s_{)}} + 1$ + c1s1 + d1se (s) где коэффициенты c1 и d1 параметризируют шумовую составляющую модели. При построении модели процесса с помощью `idproc` укажите структуру измеряемого компонента с помощью команды `Type` входной аргумент и компонент шума с помощью `NoiseTF` пара имя-значение. Например, model = idproc('P1','Kp',1,'Tp1',1,'NoiseTF',... struct('num',[1 0.1],'den',[1 0.5])) создает модель процесса y (s) = 1/( s + 1) u (s) + (s + 0,1 )/( s + 0,5) e (s)

Иногда недостаточно фиксировать коэффициенты или задавать границы параметров. Например, у вас могут быть несвязанные зависимости параметров в модели или параметры могут быть функцией другого набора параметров, которые вы хотите идентифицировать исключительно. Например, в системе «масса-пружина-демпфер» A и B оба параметра зависят от массы системы. Для достижения такой параметризации линейных моделей можно использовать серое моделирование, в котором устанавливается связь между фактическими параметрами и коэффициентами модели путем записи файла ОДУ. Дополнительные сведения см. в разделе Оценка модели «серый ящик».

Оценка линейной модели

Оценка обычно используется для создания моделей в панели инструментов идентификации системы. Выполните одну из команд оценки, указав в качестве входных аргументов измеренные данные, а также другие входные данные, необходимые для определения структуры модели. Для иллюстрации в следующем примере используется команда оценки состояния-пространства: ssest, для создания модели пространства состояний. Первый входной аргумент data определяет измеренные входные-выходные данные. Второй входной аргумент указывает порядок модели.

sys = ssest(data,4)

Функция оценки обрабатывает шумовую переменную e (t) как ошибку предсказания - остаточную часть выходного сигнала, которая не может быть приписана измеренным входам. Все алгоритмы оценки работают, чтобы минимизировать взвешенную норму e (t) на протяжении диапазона доступных измерений. Взвешивающая функция определяется природой функции H передачи шума и фокусом оценки, такой как моделирование или минимизация ошибок прогнозирования.

Оценка «черного ящика» («холодный старт»)

В оценке черного ящика необходимо указать только порядок настройки структуры модели.

sys = estimator(data,orders)

где estimator - имя команды оценки, используемой для требуемого типа модели.

Например, используется tfest для оценки моделей передаточных функций, arx для моделей полиномов структуры ARX, и procest для моделей процессов.

Первый аргумент, data, представляет данные временной или частотной области в виде iddata или idfrd объект. Второй аргумент, orders, представляет одно или несколько чисел, определения которых зависят от типа модели:

Для функций передачи, orders относится к числу полюсов и нулей.
Для моделей пространства состояний, orders относится к числу состояний.
Для моделей процессов: orders обозначает структурные элементы модели процесса, такие как количество полюсов и наличие задержки и интегратора.

При работе с приложением заказы указываются в соответствующих полях редактирования соответствующих диалоговых окон оценки модели.

Структурированные оценки

В некоторых ситуациях требуется настроить структуру требуемой модели более точно, чем это достигается простым определением заказов. В таких случаях создается шаблонная модель и настраиваются ее свойства. Затем эта модель шаблона передается в качестве входного аргумента командам оценки вместо orders.

Чтобы проиллюстрировать, следующий пример назначает начальные предполагаемые значения на нумератор и полиномиалы знаменателя модели функции передачи, налагает минимальные и максимальные границы на их ориентировочные стоимости и затем передает объект к функции оценщика.

% Initial guess for numerator
num = [1 2];
den = [1 2 1 1];
% Initial guess for the denominator 
sys = idtf(num,den);
% Set min bound on den coefficients to 0.1
sys.Structure.Denominator.Minimum = [1 0.1 0.1 0.1]; 
sysEstimated = tfest(data,sys);

Алгоритм оценки использует предоставленные начальные догадки для запуска оценки и доставляет модель, которая уважает заданные границы.

Такой шаблон модели можно использовать для настройки дополнительных свойств модели, таких как имена и единицы ввода/вывода. Если значения некоторых параметров модели изначально неизвестны, можно использовать NaNs для них в шаблоне.

Варианты оценки

Существует множество вариантов, связанных с алгоритмом оценки модели, которые конфигурируют целевую функцию оценки, начальные условия и алгоритм численного поиска, среди прочего. Для каждой команды оценки, estimator, существует соответствующая команда опций с именем estimatorOptions. Задание параметров для конкретной команды оценки, например tfest, используйте команду options, которая соответствует команде оценки, в данном случае, tfestOptions. Команда options возвращает набор опций, который затем передается в качестве входного аргумента соответствующей команде оценки.

Например, для оценки модели полинома структуры «вывод-ошибка» используется oe. Определить simulation в качестве фокуса и lsqnonlin в качестве метода поиска используется oeOptions:

load iddata1 z1
Options = oeOptions('Focus','simulation','SearchMethod','lsqnonlin');
sys= oe(z1,[2 2 1],Options);

Информация о опциях, используемых для создания расчетной модели, хранится в OptionsUsed поле модели Report собственность. Дополнительные сведения см. в разделе Отчет об оценке.

Документация