Наименьшие квадраты, в общем, это задача нахождения вектора x, который является локальным минимизатором функции, которая является суммой квадратов, возможно, подверженных некоторым ограничениям:
(x)
так, что A· x ≤ b, Aeq· x = beq, lb ≤ x ≤ ub.
Есть несколько Оптимизации решающие устройства Toolbox™, доступные для различных типов F (x) и различных типов ограничений :
| Решающее устройство | F (x) | Ограничения |
|---|---|---|
mldivide | C· x - d | Ничего |
lsqnonneg | C· x - d | x ≥ 0 |
lsqlin | C· x - d | Бордюр, линейный |
lsqnonlin | Общие сведения F (x) | Связанный |
lsqcurvefit | F (x, xdata) - ydata | Связанный |
Существует пять алгоритмов наименьших квадратов в решателях Optimization Toolbox, в дополнение к алгоритмам, используемым в mldivide:
Все алгоритмы, кроме lsqlin активные наборы являются крупномасштабными; см. Крупномасштабные и среднемасштабные алгоритмы. Общий обзор нелинейных методов наименьших квадратов см. в Dennis [8]. Конкретные подробности о методе Левенберга-Марквардта можно найти в Moré [28].
lsqlin
'interior-point' алгоритм использует алгоритм quadprog внутренней точки-выпуклой, и lsqlin
'active-set' алгоритм использует активный набор quadprog алгоритм. quadprog задача определения заключается в минимизации квадратичной функции
cTx
с учетом линейных ограничений и ограничивающих ограничений. lsqlin функция минимизирует квадратную 2-норму вектора Cx-d , подверженного линейным ограничениям и ограничивающим ограничениям. Другими словами, lsqlin минимизирует
12xT (2CTC) x + (− 2CTd) Tx + dTd.
Это вписывается в quadprog фреймворк путем установки матрицы H на 2CTC, а вектора c на (-2CTd). (Добавочный термин dTd не влияет на расположение минимума.) После этого переформулировать lsqlin проблема, quadprog вычисляет решение.
Примечание
quadprog
'interior-point-convex' алгоритм имеет два кодовых пути. Он принимает один, когда матрица Гессена H является обычной (полной) матрицей двойников, и он принимает другой, когда H является разреженной матрицей. Дополнительные сведения о разреженном типе данных см. в разделе Разреженные матрицы. Как правило, алгоритм быстрее для больших задач, которые имеют относительно мало ненулевых членов, когда вы указываете H как sparse. Аналогично, алгоритм быстрее для небольших или относительно плотных проблем, когда вы указываете H как full.
Многие методы, используемые в решателях Optimization Toolbox, основаны на областях доверия, простой, но мощной концепции оптимизации.
Чтобы понять подход доверительной области к оптимизации, рассмотрим задачу неограниченной минимизации, минимизируйте f (x), где функция принимает векторные аргументы и возвращает скаляры. Предположим, что вы находитесь в точке x в n-пространстве и хотите улучшить, т.е. переместитесь в точку с меньшим значением функции. Основная идея состоит в том, чтобы аппроксимировать f более простой функцией q, которая разумно отражает поведение функции f в окрестности N вокруг точки x. Эта окрестность является областью доверия. Пробный этап s вычисляется путем минимизации (или приблизительно минимизации) над N. Это подпроблема области доверия,
| }. | (1) |
Текущая точка обновляется до x + s, если f ( x + s ) < f (x); в противном случае текущая точка остается неизменной, и N, область доверия, уменьшается, и вычисление пробного этапа повторяется.
Ключевые вопросы при определении конкретного подхода области доверия к минимизации f (x) заключаются в том, как выбрать и вычислить аппроксимацию q (определенную в текущей точке x), как выбрать и изменить область доверия N и как точно решить подпроблему области доверия. В этом разделе рассматривается неограниченная проблема. В последующих разделах обсуждаются дополнительные осложнения из-за наличия ограничений на переменные.
В стандартном способе доверительной области ([48]) квадратичное приближение q определяется первыми двумя членами приближения Тейлора к F при x; окрестность N обычно имеет сферическую или эллипсоидальную форму. Математически обычно указывается подпроблема области доверия
| }, | (2) |
где g - градиент f в текущей точке x, H - гессеновская матрица (симметричная матрица вторых производных), D - диагональная масштабная матрица, Δ - положительный скаляр, а ∥. ∥ - 2-норма. Существуют хорошие алгоритмы для решения уравнения 2 (см. [48]); такие алгоритмы обычно включают вычисление всех собственных значений H и процесс Ньютона, применяемый к светскому уравнению
Такие алгоритмы обеспечивают точное решение уравнения 2. Однако они требуют времени, пропорционального нескольким факторизациям Н. Поэтому для проблем региона доверия необходим другой подход. Несколько аппроксимационных и эвристических стратегий, основанных на уравнении 2, были предложены в литературе ([42] и [50]). Подход аппроксимации, используемый в решателях Optimization Toolbox, заключается в ограничении подпроблемы области доверия двумерным подпространством S ([39] и [42]). После вычисления подпространства S работа по решению уравнения 2 является тривиальной, даже если необходима полная информация о собственном значении/собственном векторе (поскольку в подпространстве задача является только двумерной). Доминирующая работа теперь перешла к определению подпространства.
Двумерное подпространство S определяют с помощью процесса предварительно кондиционированного сопряженного градиента, описанного ниже. Решатель определяет S как линейное пространство, охватываемое s1 и s2, где s1 находится в направлении градиента g, а s2 является либо приближенным направлением Ньютона, т.е. решением
| (3) |
или направление отрицательной кривизны,
| (4) |
Философия, лежащая в основе этого выбора S, состоит в том, чтобы форсировать глобальную сходимость (через самое крутое направление спуска или отрицательное направление кривизны) и достичь быстрой локальной сходимости (через шаг Ньютона, когда она существует).
Эскиз неограниченной минимизации с использованием идей области доверия теперь легко дать:
Сформулируйте двухмерную подпроблему области доверия.
Решите уравнение 2, чтобы определить пробный этап s.
Если f (x + s) < f (x), то x = x + s.
Отрегулируйте Δ.
Эти четыре шага повторяются до сходимости. Измерение Δ области доверия корректируется в соответствии со стандартными правилами. В частности, он уменьшается, если стадия испытания не принимается, то есть f (x + s) ≥ f (x). Для обсуждения этого аспекта см. [46] и [49].
Решатели Optimization Toolbox рассматривают несколько важных особых случаев f со специализированными функциями: нелинейные наименьшие квадраты, квадратичные функции и линейные наименьшие квадраты. Однако лежащие в основе алгоритмические идеи те же, что и для общего случая. Эти особые случаи рассматриваются в последующих разделах.
Важным частным случаем для f (x) является нелинейная задача наименьших квадратов
| ‖ 22, | (5) |
где F (x) - векторнозначная функция с компонентом i F (x), равным fi (x). Основной метод, используемый для решения этой проблемы, является таким же, как в общем случае, описанном в документе Методы доверительной области для нелинейной минимизации. Однако для повышения эффективности используется структура нелинейной задачи наименьших квадратов. В частности, приблизительное направление Гаусса-Ньютона, т.е. решение
| (6) |
(где J - якобиан F (x)) используется для определения двумерного подпространства S. Вторые производные функции компонента fi (x) не используются.
В каждой итерации метод предварительно кондиционированных сопряженных градиентов используется для приблизительно решения нормальных уравнений, т.е.
JTF,
хотя нормальные уравнения явно не формируются.
В этом случае решаемой функцией f (x) является
=‖Cx+d‖22,
возможно, подвержены линейным ограничениям. Алгоритм генерирует строго выполнимые итерации, сходящиеся, в пределе, к локальному решению. Каждая итерация включает в себя приблизительное решение большой линейной системы (порядка n, где n - длина x). Итерационные матрицы имеют структуру матрицы C. В частности, метод предварительно кондиционированных сопряженных градиентов используется для приблизительно решения нормальных уравнений, т.е.
CTd,
хотя нормальные уравнения явно не формируются.
Метод области доверия подпространства используется для определения направления поиска. Однако вместо ограничения шага до (возможно) одного шага отражения, как в случае нелинейной минимизации, кусочно-отражающий поиск линии проводится при каждой итерации, как в квадратичном случае. Для получения подробной информации о поиске строк см. [45]. В конечном счете, линейные системы представляют подход Ньютона, фиксирующий условия оптимальности первого порядка в решении, что приводит к сильным локальным скоростям сходимости.
Функция умножения Якобиана. lsqlin может решить линейно-ограниченную задачу наименьших квадратов без явного использования матрицы C. Вместо этого он использует функцию умножения якобиана jmfun,
W = jmfun(Jinfo,Y,flag)
которые вы предоставляете. Функция должна вычислить следующие продукты для матрицы Y:
Если flag == 0 тогда W = C'*(C*Y).
Если flag > 0 тогда W = C*Y.
Если flag < 0 тогда W = C'*Y.
Это может быть полезно, если C велик, но содержит достаточно структуры, которую можно записать jmfun без явного образования C. Пример см. в разделе Функция умножения якобиана с линейными наименьшими квадратами.
Задача наименьших квадратов сводит к минимуму функцию f (x), которая является суммой квадратов.
| 22=∑iFi2 (x). | (7) |
Проблемы этого типа возникают в большом количестве практических применений, особенно тех, которые включают в себя подгонку функций модели к данным, таким как нелинейная оценка параметров. Этот тип задачи также появляется в системах управления, где цель состоит в том, чтобы выход y (x, t) следовал непрерывной модельной траектории (t) для вектора x и скаляра t. Эта задача может быть выражена как
| 2dt, | (8) |
где y (x, t) и start( t) - скалярные функции.
Дискретизируйте интеграл для получения аппроксимации
| ti)) 2, | (9) |
где ti равномерно разнесены. В этой задаче вектор F (x) равен
TM) −φ (TM)].
В этом типе проблемы остаточная ∥F ∥ (x), вероятно, будет небольшой при оптимальной, поскольку общая практика заключается в установлении реально достижимых целевых траекторий. Хотя вы можете минимизировать функцию в уравнении 7, используя общий метод неограниченной минимизации, как описано в Основах неограниченной оптимизации, некоторые характеристики задачи часто можно использовать для повышения итеративной эффективности процедуры решения. Градиентная и гессеновская матрица уравнения 7 имеют особую структуру.
Обозначают матрицу m-на-n якобиана F (x) как J (x), градиентный вектор f (x) как G (x), матрицу Гессена f (x) как H (x) и матрицу Гессена каждого Fi (x) как Di (x),
| TJ (x) + 2Q (x), | (10) |
где
(x).
Свойство матрицы Q (x) состоит в том, что когда остаточный ∥F (x) ∥ стремится к нулю, когда xk приближается к решению, то Q (x) также стремится к нулю. Так, когда ∥F (x) ∥ мал в решении, эффективным методом является использование направления Гаусса - Ньютона в качестве основы для процедуры оптимизации.
При каждой большой итерации k метод Гаусса-Ньютона получает направление поиска dk, которое является решением линейной задачи наименьших квадратов
| ) ‖ 22. | (11) |
Направление, полученное из этого метода, эквивалентно направлению Ньютона, когда члены Q (x) = 0. Алгоритм может использовать направление поиска dk как часть стратегии поиска строки, чтобы гарантировать, что функция f (x) уменьшается при каждой итерации.
Метод Гаусса - Ньютона часто сталкивается с проблемами, когда член второго порядка Q (x) неиглибибельен. Метод Левенберга - Марквардта преодолевает эту проблему.
Метод Левенберга - Марквардта (см. [25] и [27]) использует направление поиска, которое является решением линейного набора уравнений
| xk) TF (xk), | (12) |
или, необязательно, уравнений
| J (xk) TF (xk), | (13) |
где скаляр λ k управляет как величиной, так и направлением dk, и diag(A) означает матрицу диагональных членов в A. Установка опции ScaleProblem кому 'none' для выбора уравнения 12 или набора ScaleProblem кому 'Jacobian' для выбора уравнения 13.
Начальное значение параметра λ 0 задается с помощью InitDamping вариант. Иногда, 0.01 значение по умолчанию для этого параметра может быть неподходящим. Если вы обнаружите, что алгоритм Левенберга-Марквардта делает мало начального прогресса, попробуйте установить InitDamping в значение, отличное от значения по умолчанию, например 1e2.
Когда λ k равно нулю, направление dk идентично направлению метода Гаусса-Ньютона. Поскольку λ k стремится к бесконечности, dk стремится к самому крутому направлению спуска, а величина стремится к нулю. Следовательно, для некоторых достаточно больших λ k верен термин F (xk + dk) < F (xk). Поэтому можно управлять термином λ k, чтобы обеспечить спуск даже тогда, когда алгоритм встречает члены второго порядка, которые ограничивают эффективность метода Гаусса - Ньютона. Когда шаг успешен (даёт меньшее значение функции), алгоритм устанавливает λ k + 1 = λ k/10. Когда шаг оказывается неудачным, алгоритм устанавливает λ k + 1 = λ k * 10.
Внутри алгоритма Левенберга-Марквардта используется допуск оптимальности (критерий остановки) 1e-4 умножает допуск функции.
Метод Левенберга - Марквардта, таким образом, использует направление поиска, являющееся пересечением между направлением Гаусса - Ньютона и наиболее крутым направлением спуска.
Еще одно преимущество метода Левенберга-Марквардта заключается в том, что якобиан J является дефицитным по рангу. В этом случае метод Гаусса-Ньютона может иметь численные проблемы, поскольку проблема минимизации в уравнении 11 является неуместной. Напротив, метод Левенберга - Марквардта имеет полный ранг на каждой итерации, и, следовательно, избегает этих проблем.
На следующем рисунке показаны итерации метода Левенберга-Марквардта при минимизации функции Розенброка, заведомо трудной задачи минимизации, которая находится в форме наименьших квадратов.
Метод Левенберга-Марквардта о функции Розенброка
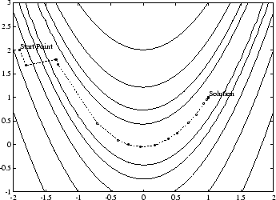
Более полное описание этого рисунка, включая сценарии, генерирующие итеративные точки, см. в разделе Минимизация функции банана.
Когда проблема содержит связанные ограничения, lsqcurvefit и lsqnonlin изменить итерации Левенберга-Марквардта. Если предлагаемая итеративная точка x лежит за пределами границ, алгоритм проецирует шаг на ближайшую осуществимую точку. Другими словами, когда P определен как оператор проекции, который проецирует неосуществимые точки на осуществимую область, алгоритм изменяет предложенную точку x на P (x). По определению, оператор проекции P работает на каждом компоненте xi независимо в соответствии с
ubixiotherwise
или, эквивалентно,
, ubi).
Алгоритм изменяет критерий остановки для меры оптимальности первого порядка. Пусть x - предлагаемая итеративная точка. В неограниченном случае критерием остановки является
| ∞≤tol, | (14) |
где tol - значение допуска оптимальности, которое равно 1e-4*FunctionTolerance. В ограниченном случае критерием остановки является
| ∞2≤tol‖∇f (x) ‖ ∞. | (15) |
Чтобы понять этот критерий, сначала обратите внимание, что если x находится внутри осуществимой области, то оператор P не имеет эффекта. Таким образом, критерий остановки становится
∞2≤tol‖∇f (x) ‖ ∞,
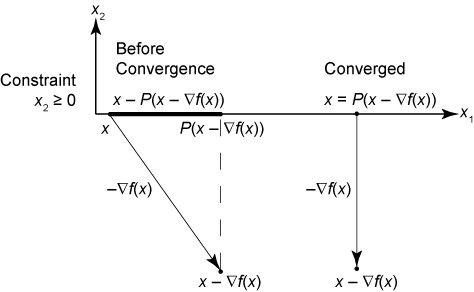
который совпадает с исходным критерием остановки без ограничений, ∞≤tol. Если граничная зависимость активна, что означает x - ∇f (x) неосуществимо, то в точке, где алгоритм должен остановиться, градиент в точке на границе перпендикулярен границе. Поэтому точка x равна P (x - ∇f (x)), проекции самого крутого шага спуска, как показано на следующем рисунке.
Условие остановки Левенберга-Марквардта
lsqcurvefit | lsqlin | lsqnonlin | lsqnonneg | quadprog