Зубчатый механизм, позволяющий приводным валам вращаться на разных скоростях
Simscape/трансмиссия/зубчатые колеса
Дифференциальный блок представляет собой зубчатый механизм, который позволяет ведомым валам вращаться на разных скоростях. Дифференциалы распространены в автомобилях, где они позволяют различным колесам вращаться на разных скоростях при повороте. Отверстия D, S1 и S2 представляют продольный карданный вал и вал солнечной шестерни дифференциала соответственно. Любой из валов может приводить в движение два других.
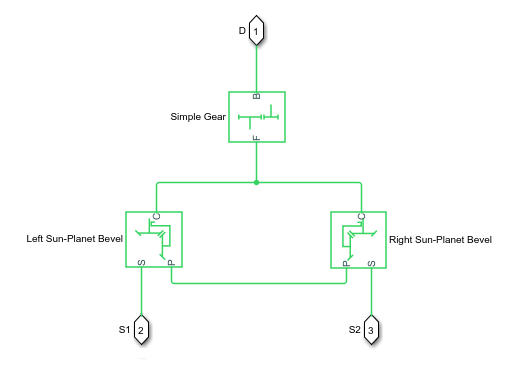
Блок моделирует отличительный механизм как структурный компонент на основе Простых блоков Simscape™ Driveline™ Скоса Механизма и Планеты Солнца. На рисунке показана эквивалентная блок-схема для дифференциального блока.
Чтобы повысить точность модели зубчатого колеса, задайте такие свойства, как инерция зубчатого колеса, потери сетки и потери вязкости. По умолчанию предполагается, что инерция передачи и потери вязкости являются незначительными. Блок позволяет задать инерции зубчатого колеса и внутренних сателлитов. Для моделирования инерций внешних зубчатых колес подключите блоки Simscape Inertia к портам D, S1 и S2.
Можно смоделировать влияние теплового потока и изменения температуры, включив дополнительный тепловой порт. Чтобы включить порт, задайте для модели трения значение Temperature-dependent efficiency.
Дифференциал накладывает одну кинематическую зависимость на три соединенные оси, так что
где:
ωS1 - скорость вала 1 солнечной шестерни.
ωS2 - скорость вала 2 солнечной шестерни.
Отрицательные значения означают, что дифференциал остается от осевой линии. Три степени свободы уменьшаются до двух независимых степеней свободы. Зубчатые пары (1,2) = (S, S) и (C, D). C является носителем.
Сумма поперечных движений представляет собой преобразованное продольное движение. Разность боковых движений, ωS2, не зависит от продольного движения. Общее движение боковых валов является наложением этих двух независимых степеней свободы, которые имеют такое физическое значение:
Продольная степень свободы эквивалентна двум боковым валам, вращающимся с одной и той же угловой скоростью имеющим
Дифференциальная степень свободы эквивалентна удержанию продольного приводного вала заблокированным, 0, где startD - скорость приводного вала, в то время как боковые валы вращаются относительно друг друга в противоположных направлениях− ωS2.
Крутящие моменты поперечной оси ограничены крутящим моментом продольной оси так, что суммарный расход мощности равен нулю:
Плосс = 0,
где:
τS1 и τS2 - крутящие моменты вдоль боковых осей.
δ D - продольный крутящий момент.
Плосс - это потеря мощности.
Когда кинематические и силовые ограничения объединены, идеальный вариант дает
ωS1 + ωS2,
где gD - передаточное число продольного карданного вала.
Эффективное ограничение дифференциального блока состоит из двух субограничений конического зубчатого колеса солнечной планеты.
Первое подограничение обусловлено присоединением двух конических шестерен солнечная планета к водилу:
gSP2gSP1,
где gSP1 и gSP2 - передаточные числа зубчатых колес солнечной планеты.
Вторая зависимость обусловлена присоединением носителя к продольному карданному валу:
gDλ C.
Передаточные отношения солнечных планет нижележащих конических зубчатых колес солнечных планет в пересчете на радиусы r зубчатых колес солнечных планет составляют:
Дифференциальный блок реализован с = 1, оставляя gD свободным для регулировки.
В неидеальном случае, startloss ≠ 0. Дополнительные сведения см. в разделе Модель зубчатых колес с потерями.
Зубчатые колеса считаются жесткими.
Кулонское трение замедляет моделирование. Дополнительные сведения см. в разделе Корректировка точности модели.
Фрикционная муфта диска | Простая передача | Скос Солнца-Планеты