Exponenta Banner
exponenta event banner

h2hinfsyn

Смешанный синтез H2/H∞ с ограничениями размещения региональных полюсов

свернуть все на странице

Синтаксис

[K, CL, normz, info] = h2hinfsyn (P,Nmeas,Ncon,Nz2,Wz,Name,Value)

Описание

пример

[K,CL,normz,info] = h2hinfsyn(P,Nmeas,Ncon,Nz2,Wz,Name,Value) использует методы LMI для вычисления закона управления с выходной обратной связью u = K (s) y для задачи управления, показанной на следующей иллюстрации.

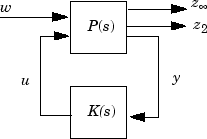
Завод LTI P имеет секционированную форму state-space, заданную

x˙=Ax+B1w+B2u,z∞=C1x+D11w+D12u,z2=C2x+D21w+D22u,y=Cyx+Dy1w+Dy2u.

Результирующий контроллер K:

  • Сохраняет H∞ норму G передаточной функции от w до z∞ ниже значения, указанного с помощью Name,Value аргумент 'HINFMAX'.

  • Сохраняет норму H2 H передаточной функции от w до z2 ниже значения, указанного с помощью Name,Value аргумент 'H2MAX'.

  • Минимизирует критерий компромисса формы

    W1G2+W2H2,

    где W1 и W2 - первая и вторая записи в векторе Wz.

  • Размещение полюсов с замкнутым контуром в области LMI, указанной с помощью Name,Value аргумент 'REGION'.

Использовать входные аргументы Nmeas, Ncon, и Nz2 для задания количества сигналов в y, u и z2 соответственно. Вы можете использовать дополнительные Name,Value для задания дополнительных опций вычисления.

Примеры

свернуть все

Открыть сценарий в реальном времени

При наличии установки сконструируйте контроллер таким образом, чтобы полюса замкнутой системы лежали в полуплоскости, определяемой Re (s) < -1 .

Вы можете определить эту область для размещения полюса с помощью интерактивного lmireg команда. Для этого

  1. Войти region = lmireg в командной строке MATLAB ®.

  2. Войти h для задания зависимости полуплоскости.

  3. Войти l для задания левой полуплоскости.

  4. Войти -1 чтобы указать, что отсечка для области x0 = –1.

  5. Войти q для выхода и создания области LMI.

Область, созданная этим процессом, эквивалентна следующим командам. (Дополнительные сведения см. в разделе lmireg справочная страница.) 

RealPart = -1; 
region = [-2*RealPart + 1i 1];

Укажите модель завода. В этом примере используется установка с двумя входами и тремя выходами. Предположим, что установка содержит один управляющий сигнал и один измерительный сигнал (nmeas = ncont = 1) и разделяется таким образом, что эти сигналы являются последними входными и выходными соответственно.

A = [1 0;2 1]; 
B = [1 1;1 0]; 
C = [1 1;1 1;1 1]; 
D = zeros(3,2);
P = ss(A,B,C,D);

Вычислить контроллер для P использование области LMI для ограничения расположения полюсов с замкнутым контуром. Наложить ограничение нормы H2 на один сигнал (Nz2 = 1) и придать H2 и H∞ нормам равный вес. 

ncont = 1;
nmeas = 1;
Nz2 = 1 ;
Wz = [0 0];
[K,CL] = h2hinfsyn(P,nmeas,ncont,Nz2,Wz,'Region',region); 
 Solver for LMI feasibility problems L(x) < R(x)
    This solver minimizes  t  subject to  L(x) < R(x) + t*I
    The best value of t should be negative for feasibility

 Iteration   :    Best value of t so far 
 
     1                        7.368392
     2                      -95.362851

 Result:  best value of t:   -95.362851
          f-radius saturation:  0.009% of R =  1.00e+08

Убедитесь, что полюса замкнутой системы имеют Re (ы) < -1 .

pole(CL)
ans = 4×1 complex

  -1.6786 + 3.2056i
  -1.6786 - 3.2056i
  -1.5563 + 1.6678i
  -1.5563 - 1.6678i

Изменить собственные значения с замкнутым контуром можно и дальше. RealPart. Можно также определить другие области размещения полюсов. Например, поместите полюса так, чтобы Re (ы) упал в полоску комплексной плоскости -5 < Re (ы) < -3. Чтобы определить эту область, используйтеlmireg интерактивно для создания reg1 задание Re (s) > -5, иreg2 указание Re (s) < -3. Затем введитеregion = lmireg(reg1,reg2) для определения пересечения этих двух областей. Следующий код эквивалентен. 

LeftRealPart = -5; 
RightRealPart = -3;
region = [-2*RightRealPart + 1i 0 1 0;
           0 2*LeftRealPart + 1i 0 -1];

Вычислите новый контроллер и подтвердите расположение полюсов с замкнутым контуром.

[K,CL] = h2hinfsyn(P,nmeas,ncont,Nz2,Wz,'Region',region); 
 Solver for LMI feasibility problems L(x) < R(x)
    This solver minimizes  t  subject to  L(x) < R(x) + t*I
    The best value of t should be negative for feasibility

 Iteration   :    Best value of t so far 
 
     1                       17.688394
     2                        1.074621
     3                      -13.502955

 Result:  best value of t:   -13.502955
          f-radius saturation:  0.048% of R =  1.00e+08
 

pole(CL)
ans = 4×1 complex

  -3.7864 + 4.9210i
  -3.7864 - 4.9210i
  -3.7752 + 3.6186i
  -3.7752 - 3.6186i

Входные аргументы

свернуть все

Завод, указанный как модель LTI, например tf или ss модель. P должна быть моделью непрерывного времени.

Количество измерительных сигналов, указанное как положительное целое число. Это значение представляет собой количество сигналов в y.

Число управляющих сигналов, указанное как положительное целое число. Это значение является количеством сигналов в u.

Число сигналов, на которые распространяется ограничение по норме H2, определяемое как положительное целое число. Это значение представляет собой количество сигналов в z2. Если общее количество выходов P является Nout, то первый Nout - Nz2 - Nmeas выходы P подчиняются ограничению по H∞ норме.

Веса для H∞ и производительности H2, указанные как вектор 1 на 2 формы [Winf,W2].

Аргументы пары «имя-значение»

Укажите дополнительные пары, разделенные запятыми Name,Value аргументы. Name является именем аргумента и Value - соответствующее значение. Name должен отображаться внутри кавычек. Можно указать несколько аргументов пары имен и значений в любом порядке как Name1,Value1,...,NameN,ValueN.

Пример: 'REGION',reg,'H2MAX',1,'HINFMAX',1,'DISPLAY','on'

Область размещения полюсов, заданная как разделенная запятыми пара, состоящая из 'REGION' и матрица формы [L,M]. Эта матрица определяет область размещения полюсов как:

{z: L + zM + z MT < 0}.

Создание матрицы с помощью lmireg. Область LMI по умолчанию для размещения полюсов, заданная пустой матрицей [], - открытая левая полуплоскость, обеспечивающая только стабильность по замкнутому контуру.

Верхняя граница на норме H2 передаточной функции от w до z2, заданная как разделенная запятыми пара, состоящая из 'H2MAX' и положительное скалярное значение или Inf. Значение по умолчанию Inf эквивалентно установке предела на ноль и вызывает h2hinfsyn свести к минимуму H2 норму с учетом критерия компромисса.

Пример: 'H2MAX',1

Верхняя граница в норме H∞ передаточной функции от w до z∞, заданная как разделенная запятыми пара, состоящая из 'HINFMAX' и положительное скалярное значение или Inf. Значение по умолчанию Inf эквивалентно установке предела на ноль и вызывает h2hinfsyn свести к минимуму H∞ норму с учетом критерия компромисса.

Пример: 'HINFMAX',1

Привязано к норме на матрице DK канала контроллера, заданной как разделенная запятыми пара, состоящая из 'DKMAX' и неотрицательное скалярное значение. Чтобы сделать контроллер K строго правильно, комплект 'DKMAX' в 0.

Пример: 'DKMAX',0

Желаемая относительная точность по оптимальному значению критерия компромисса, определяемого как пара, разделенная запятыми, состоящая из: 'TOL' и положительное скалярное значение.

Переключатель для отображения на экране синтезирующей информации, заданной как разделенная запятыми пара, состоящая из 'DISPLAY' и либо 'on' или 'off'.

Выходные аргументы

свернуть все

Оптимальный контроллер вывода-обратной связи, возвращаемый как state-space (ss) модель с Nmeas входные данные и Ncon выходы.

Замкнутая система с синтезированным контроллером, возвращаемая в виде состояния-пространства (ss) модель. Система с замкнутым контуром CL = lft(P,K).

Нормы замкнутого цикла, возвращаемые как вектор 1 на 2. Записи в этом векторе, соответственно, следующие:

  • Норма H∞ функции передачи с обратной связью от w до z∞.

  • Норма H2 функции передачи с обратной связью от w до z2.

Решения условий разрешимости LMI, возвращенные в виде структуры, содержащей следующие поля:

  • R - Раствор R условия разрешимости LMI

  • S - Раствор S условия разрешимости LMI

Совет

  • Не выбирайте функции взвешивания с полюсами, очень близкими к s = 0 (z = 1 для дискретно-временных систем). Например, хотя может показаться разумным выбрать W = 1/s, чтобы принудить нулевую ошибку установившегося состояния, это вводит неустойчивый полюс, который не может быть стабилизирован, вызывая сбой синтеза. Вместо этого выберите W = 1/( s + δ). Значение δ должно быть малым, но не очень малым по сравнению с динамикой системы. Например, для наилучших числовых результатов, если целевая частота пересечения составляет около 1 рад/с, выберите δ = 0,0001 или 0,001. Аналогично, в дискретное время выбирайте время выборки таким образом, чтобы динамика системы и взвешивания была не более чем на десятилетие или два ниже частоты Найквиста.

Ссылки

[1] Chilali, M. и П. Гэхинет, «H ∞ дизайн с ограничениями размещения поляка: подход LMI», AUT сделки IEEE. Контр., 41 (1995), стр. 358-367.

[2] Шерер, С., «Смешанный H2/H-infinity контроль», Тенденции в области контроля: европейская перспектива, Springer-Verlag (1995), стр. 173-216.

См. также

|

Представлен до R2006a

Документация по инструментам надежного управления

Поддержка