В некоторых ситуациях невозможно точно описать образец данных с помощью параметрического распределения. Вместо этого по данным должна оцениваться функция плотности вероятности (pdf) или кумулятивная функция распределения (cdf). Toolbox™ статистики и машинного обучения предоставляет несколько вариантов оценки pdf или cdf на основе выборочных данных.
Распределение ядра дает непараметрическую оценку плотности вероятности, которая адаптируется к данным, а не выбирает плотность с определенной параметрической формой и оценивает параметры. Это распределение определяется средством оценки плотности ядра, функцией сглаживания, которая определяет форму кривой, используемой для генерации pdf, и значением полосы пропускания, которое управляет гладкостью результирующей кривой плотности.
Подобно гистограмме, распределение ядра строит функцию для представления распределения вероятности с использованием данных выборки. Но в отличие от гистограммы, которая помещает значения в дискретные ячейки, распределение ядра суммирует функции сглаживания компонентов для каждого значения данных, чтобы получить гладкую непрерывную кривую вероятности. На следующем графике показано визуальное сравнение гистограммы и распределения ядра, сгенерированного из одних и тех же данных выборки.
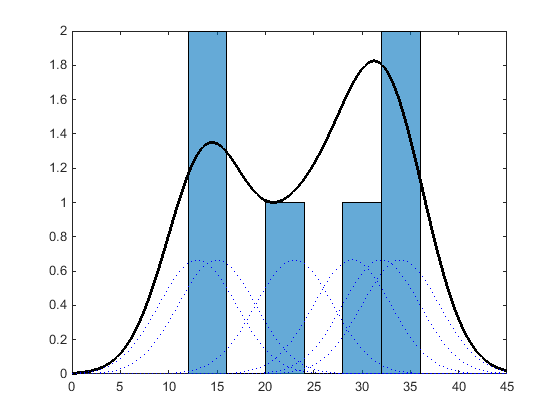
Гистограмма представляет распределение вероятности путем установления ячеек и размещения каждого значения данных в соответствующем ячейке. Из-за такого подхода к подсчету ячеек гистограмма создает дискретную функцию плотности вероятности. Это может быть непригодным для определенных приложений, таких как генерация случайных чисел из подобранного распределения.
Альтернативно, распределение ядра строит функцию плотности вероятности (pdf), создавая индивидуальную кривую плотности вероятности для каждого значения данных, затем суммируя гладкие кривые. Этот подход создает одну плавную непрерывную функцию плотности вероятности для набора данных.
Дополнительные сведения о дистрибутивах ядра см. в разделе Дистрибутив ядра. Сведения о работе с дистрибутивом ядра см. в разделе Using KernelDistribution Objects и ksdensity.
Эмпирическая кумулятивная функция распределения (ecdf) оценивает cdf случайной величины, присваивая равную вероятность каждому наблюдению в выборке. Из-за этого подхода ecdf является дискретной кумулятивной функцией распределения, которая создает точное совпадение между ecdf и распределением данных выборки.
Следующий график показывает визуальное сравнение ecdf 20 случайных чисел, сгенерированных из стандартного нормального распределения, и теоретического cdf стандартного нормального распределения. Кружки указывают значение ecdf, рассчитанное в каждой точке данных образца. Пунктирная линия, которая проходит через каждую окружность, визуально представляет ecdf, хотя ecdf не является непрерывной функцией. Сплошная линия показывает теоретический cdf стандартного нормального распределения, из которого были взяты случайные числа в данных выборки.
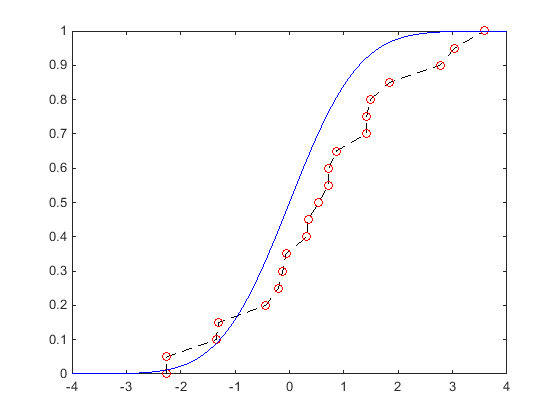
Ecdf по форме аналогичен теоретическому cdf, хотя и не является точным совпадением. Вместо этого ecdf является точным совпадением с данными выборки. Ecdf является дискретной функцией и не является гладкой, особенно в хвостах, где данные могут быть разреженными. Можно сгладить распределение с помощью хвостов Парето, используя paretotails функция.
Дополнительные сведения и дополнительные параметры синтаксиса см. в разделе ecdf. Сведения о построении непрерывной функции на основе значений cdf, вычисленных на основе данных выборки, см. в разделе Кусочно-линейное распределение.
Кусочно-линейное распределение оценивает общий cdf для данных выборки, вычисляя значение cdf в каждой отдельной точке, а затем линейно соединяя эти значения с образованием непрерывной кривой.
Следующий график показывает cdf для кусочно-линейного распределения на основе выборки измерений веса пациентов больницы. Круги представляют каждую отдельную точку данных (измерение веса). Черная линия, проходящая через каждую точку данных, представляет кусочно-линейное распределение cdf для данных выборки.
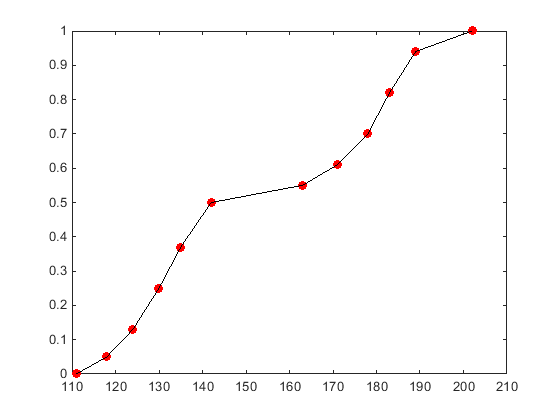
Кусочно-линейное распределение линейно соединяет значения cdf, рассчитанные в каждой точке данных выборки, с образованием непрерывной кривой. Напротив, эмпирическая кумулятивная функция распределения, построенная с использованием ecdf функция создает дискретный cdf. Например, случайные числа, сгенерированные из ecdf, могут включать только значения x, содержащиеся в исходных данных выборки. Случайные числа, генерируемые кусочно-линейным распределением, могут включать любое значение x между нижней и верхней границами данных выборки.
Поскольку кусочно-линейное распределение cdf строится из значений, содержащихся в данных выборки, результирующая кривая часто не является гладкой, особенно в хвостах, где данные могут быть разреженными. Можно сгладить распределение с помощью хвостов Парето, используя paretotails функция.
Сведения о работе с кусочно-линейным распределением см. в разделе Использование PiecewiseLinearDistribution Объекты.
Хвосты Парето используют кусочный подход для улучшения посадки непараметрического cdf путем сглаживания хвостов распределения. Можно подгонять распределение ядра, эмпирический cdf или определяемый пользователем оценщик к средним значениям данных, а затем подгонять обобщенные кривые распределения Парето к хвостам. Этот метод особенно полезен, когда данные образца разрежены в хвостах.
Следующий график показывает эмпирический cdf (ecdf) выборки данных, содержащей 20 случайных чисел. Сплошная линия представляет ecdf, а пунктирная линия представляет эмпирический cdf с хвостами Парето, прилегающими к нижнему и верхнему 10 процентам данных. Окружности обозначают границы для нижнего и верхнего 10 процентов данных.
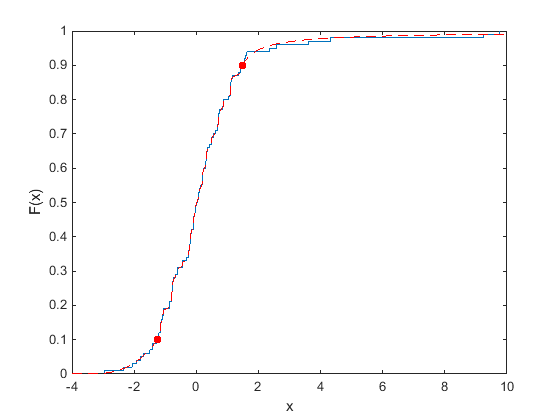
Подгонка хвостов Парето к нижнему и верхнему 10 процентам данных образца делает cdf более гладким в хвостах, где данные разрежены. Дополнительные сведения о работе с хвостами Парето см. в разделе paretotails.
Треугольное распределение обеспечивает упрощенное представление вероятностного распределения при наличии ограниченных данных выборки. Это непрерывное распределение параметризуется нижним пределом, положением пика и верхним пределом. Эти точки линейно соединены для оценки pdf данных образца. В качестве местоположения пика можно использовать среднее значение, медиану или режим данных.
На следующем графике показано треугольное распределение pdf случайной выборки из 10 целых чисел от 0 до 5. Нижний предел - наименьшее целое число в выборке данных, а верхний предел - наибольшее целое число. Пик для этого графика находится в режиме или наиболее часто встречающемся значении в данных выборки.
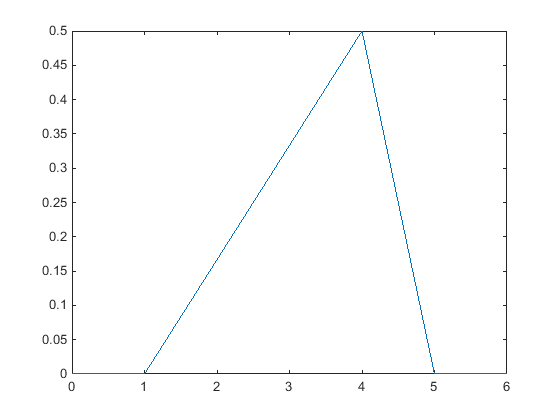
Бизнес-приложения, такие как моделирование и управление проектами, иногда используют треугольное распределение для создания моделей при наличии ограниченных данных образцов. Дополнительные сведения см. в разделе Треугольное распределение.
ecdf | ksdensity | paretotails