Запас по амплитуде, запас по фазе и частоты среза
margin( строит графики Bode-отклика sys)sys на экране и указывает коэффициент усиления и запасов по фазе на графике. Запасы по амплитуде выражены в дБ на графике.
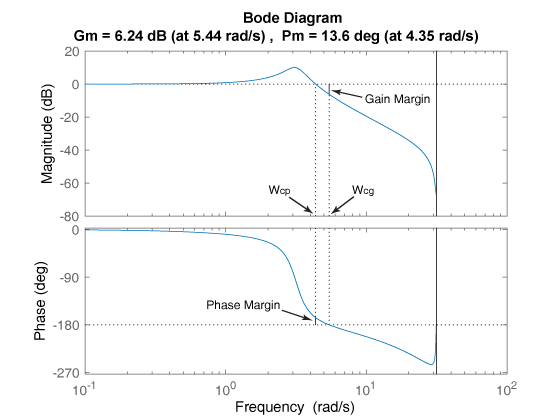
Сплошные вертикальные линии отмечают запас по амплитуде и запас по фазе. Штриховые вертикальные линии указывают местоположение Wcp, частоту, на которой измеряется запас по фазе, и Wcg, частоту, на которой измеряется запас по амплитуде. Название графика включает величину и расположение запаса по амплитуде и фазе.
Gm и Pm системы указывают относительную устойчивость системы с обратной связью, образованной применением модуля отрицательной обратной связи к sys, как показано на следующем рисунке.
Gm - величина отклонения усиления, необходимая для создания цикла единицы усиления на частоте Wcg где угол фазы -180 ° (по модулю 360 °). Другими словами, запас по амплитуде равен 1/ g, если g - коэффициент усиления на частоте фазы -180 °. Точно так же запас по фазе является различием между фазой отклика и -180 °, когда коэффициент усиления цикла равен 1,0.
Частотный Wcp при котором величина равна 1,0, называется частотой единства-усиления или частотой среза усиления. Как правило, запасы по амплитуде от трех или более в сочетании с запасами по фазе от 30 ° до 60 ° приводят к разумным компромиссам между шириной полосы и стабильностью.
[ возвращает запас по амплитуде Gm,Pm,Wcg,Wcp] = margin(sys)Gm в абсолютных модулях, запас по фазе Pmи соответствующие частоты Wcg и Wcp, из sys. Wcg - частота, на которой измеряется запас по амплитуде, представляющий собой частоту пересечения фазы -180 °. Wcp - частота, на которой измеряется запас по фазе, который является 0-dB частотой пересечения коэффициента усиления. Эти частоты выражены в радианах/ TimeUnit, где TimeUnit- модуль, заданная в TimeUnit свойство sys. Когда sys имеет несколько кроссоверов, margin возвращает наименьшие запасы по усилению и фазе и соответствующие частоты.
[ выводит коэффициент усиления и запасов по фазе из данных частотной характеристики. Предоставьте данные о усилении Gm,Pm,Wcg,Wcp] = margin(mag,phase,w)mag в абсолютных модулях и данных фазы phase в степенях. Можно задать вектор частоты w в любых модулях и margin возвращает Wcg и Wcp в тех же модулях.
В данном примере создайте непрерывную передаточную функцию.
sys = tf(1,[1 2 1 0])
sys =
1
---------------
s^3 + 2 s^2 + s
Continuous-time transfer function.
Отобразите коэффициент усиления и запасов по фазе графически.
margin(sys)
Отображаемые в заголовке запасы по амплитуде (6,02 дБ) и запас по фазе (21,4 ° С) отмечены сплошными вертикальными линиями. Штриховые вертикальные линии указывают местоположение Wcg, частоту, на которой измеряется запас по амплитуде и Wcp, частоту, на которой измеряется запас по фазе.
В данном примере создайте передаточную функцию в дискретном времени.
sys = tf([0.04798 0.0464],[1 -1.81 0.9048],0.1)
sys = 0.04798 z + 0.0464 --------------------- z^2 - 1.81 z + 0.9048 Sample time: 0.1 seconds Discrete-time transfer function.
Вычислите запас по амплитуде, запас по фазе и частоты.
[Gm,Pm,Wcg,Wcp] = margin(sys)
Gm = 2.0517
Pm = 13.5711
Wcg = 5.4374
Wcp = 4.3544
Результаты показывают, что изменение коэффициента усиления более 2,05 дБ при частоте среза фаз 5,43 рад/с приведет к нестабильности системы. Аналогично изменение фазы более чем на 13,57 степени при частоте среза коэффициента усиления 4,35 рад/с приведет к потере устойчивости системы.
В данном примере загружают данные частотной характеристики разомкнутого контура системы, состоящие из величин (m) и значений фазы (p), измеренных на частотах w.
load('openLoopFRD.mat','p','m','w');
Вычислите запасы по усилению и фазе.
[Gm,Pm,Wcg,Wcp] = margin(m,p,w)
Gm = 0.6249
Pm = 48.9853
Wcg = 1.2732
Wcp = 1.5197
В данном примере загрузите invertedPendulumArray.mat, который содержит массив 3х3 инвертированных моделей маятника. Масса маятника изменяется при перемещении от модели к модели вдоль одного столбца sys, и длина маятника изменяется, когда вы перемещаетесь вдоль одна строка. Используемые значения массы составляют 100g, 200g и 300g, а используемые длины маятника составляют 3m, 2m и 1m соответственно.
load('invertedPendulumArray.mat','sys'); size(sys)
3x3 array of transfer functions. Each model has 1 outputs and 1 inputs.
Найдите запас по амплитуде и фазе для всех моделей массива.
[Gm,Pm] = margin(sys)
Gm = 3×3
0.9800 0.9800 0.9800
0.9800 0.9800 0.9800
0.9800 0.9800 0.9800
Pm = 3×3
-11.3565 -11.3898 -11.4228
-11.3842 -11.4088 -11.4333
-11.4020 -11.4208 -11.4396
margin возвращает два массива, Gm и Pm, в котором каждая запись является значениями запаса по амплитуде и фазе соответствующей записи в sys. Например, коэффициент запаса по амплитуде и фазе модели с весом маятника 100 г и длиной 2 м Gm(1,2) и Pm(1,2), соответственно.
Когда вы используете margin(mag,phase,w), margin полагается на интерполяцию для аппроксимации полей, которые обычно дают менее точные результаты. Для примера, если нет 0-dB пересечения в w область значений, margin возвращает запас по фазе Inf. Поэтому, если у вас есть аналитическая модель sys, использование [Gm,Pm,Wcg,Wcp] = margin(sys) является более надежным способом получения полей.