Библиотека Matrices и Linear Algebra предоставляет три больших подмножества, содержащих блоки для линейной алгебры; Линейные системные решатели, матричные факторизации и обратные матрицы. Четвертая библиотека, Матричные Операции, предоставляет другие важные блоки для работы с матрицами.
Библиотека Линейная Система Solvers предоставляет следующие блоки для решения системы линейных уравнений AX = B:
Некоторые блоки предлагают особые сильные стороны для определенных классов задач. Для примера блок Холецкого Решателя адаптирован для квадратной эрмитовой положительно определенной матрицы А, в то время как Backward Substitution блок подходит для верхней треугольной матрицы А.
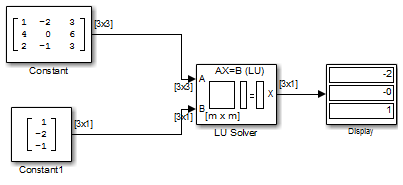
В следующей ex_lusolver_tut модели блок LU Solver решает уравнение A x = b, где
и находит x, чтобы быть вектором [-2 0 1]'.
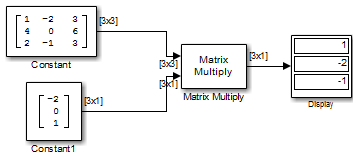
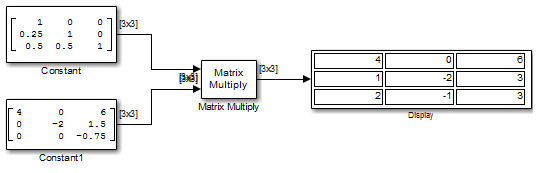
Можно проверить решение с помощью блока Multiply матрицы для выполнения x умножения A, как показано на следующей ex_matrixmultiply_tut1 модели.
Библиотека Matrix Factorizations предоставляет следующие блоки для факторинга различных видов матриц:
Некоторые блоки предлагают особые сильные стороны для определенных классов задач. Для примера Факторизации Холесского блок подходит для факторизации эрмитовой положительно определенной матрицы в треугольные компоненты, в то время как QR-факторизация подходит для факторизации прямоугольной матрицы в унитарные и верхние треугольные компоненты.
В следующей ex_lufactorization_tut модели блок LU-факторизация множит матрицу Ap в верхние и нижние треугольные подматрицы U и L, где Ap является строкой, эквивалентной входной матрице А, где
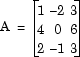
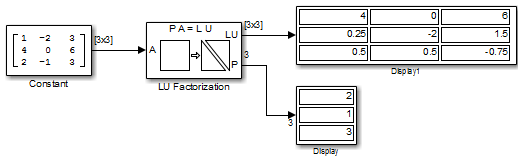
Нижний выход LU-факторизации, P, является вектором индекса сочетания, который указывает, что факторизованная матричная Ap сгенерирована из A путем обмена первой и второй строками.
Верхний выход LU-факторизации, LU, является составной матрицей, содержащей два подматричных фактора, U и L, чей продукт LU равен Ap.
Можно проверить, что LU = Ap с блоком Multiply, как показано на следующей ex_matrixmultiply_tut2 модели.
Библиотека Обратные матрицы предоставляет следующие блоки для инвертирования различных видов матриц:
В следующей ex_luinverse_tut модели блок LU Inverse вычисляет обратную матрицу А, где
а затем формирует продукт A-1A, которая приводит к единичной матрице порядка 3, как и ожидалось.
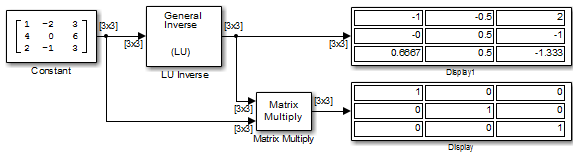
Как показано выше, вычисленная обратная величина