Этот пример показывает, как оценить допущения модели GARCH путем выполнения остаточной диагностики с помощью приложения Econometric Modeler. Набор данных, хранящийся в CAPMuniverse.mat, содержит рыночные данные по суточным возвратам акций и денежных средств (денежный рынок) за период с 1 января 2000 года по 7 ноября 2005 года. Рассмотрите моделирование возвратов рыночного индекса (MARKET).
В командной строке загрузите CAPMuniverse.mat набор данных.
load CAPMuniverseСерия находится в расписании AssetsTimeTable.
В командной строке откройте приложение Econometric Modeler.
econometricModeler
Также откройте приложение из галереи Apps (см. Econometric Modeler).
Импортируйте AssetsTimeTable в приложение:
На вкладке Econometric Modeler, в разделе Import, нажмите.![]()
В Import Data окне в столбце Import? установите флажок для AssetsTimeTable переменная.
Нажмите Import.
Индексные переменные, включая MARKET, появится на панели Time Series, а график временных рядов, содержащий все ряды, появится в Time Series Plot(APPL) окне рисунка.
Постройте график ряда рыночных индексов двойным кликом мыши на MARKET временные ряды на панели Time Series.
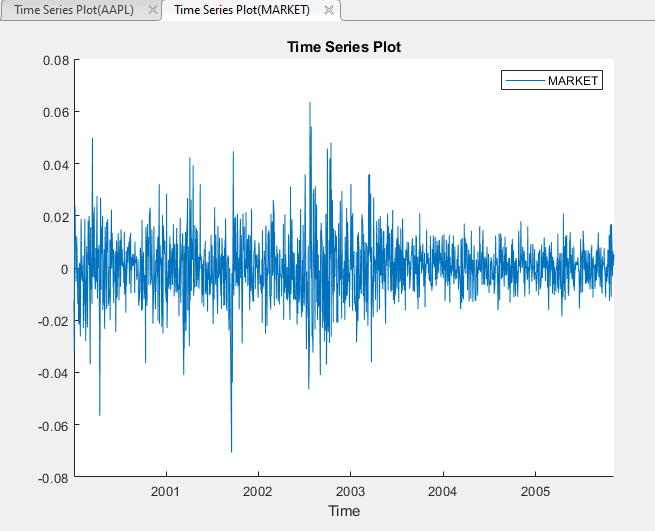
Серия, по-видимому, колеблется вокруг y = 0 и показывает кластеризацию волатильности. Рассмотрим модель GARCH (1,1) без среднего смещения для ряда.
Задайте модель GARCH (1,1) без среднего смещения.
На панели Time Series выберите MARKET.
На вкладке Econometric Modeler, в разделе Models, щелкните стреле, чтобы отобразить галерею моделей.
В галерее моделей, в GARCH Models разделе, нажмите GARCH.
В диалоговом окне GARCH Model Parameters на вкладке Lag Order:
Установите GARCH Degree значение 1.
Установите ARCH Degree значение 1.
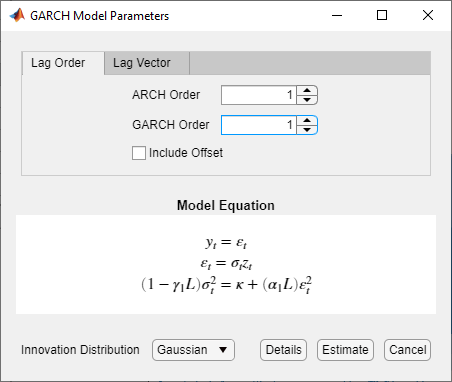
Нажмите Estimate.
Переменная модели GARCH_MARKET появится на панели Models, его значение появится на панели Preview, а сводные данные оценок появятся в Model Summary(GARCH_MARKET) документе.
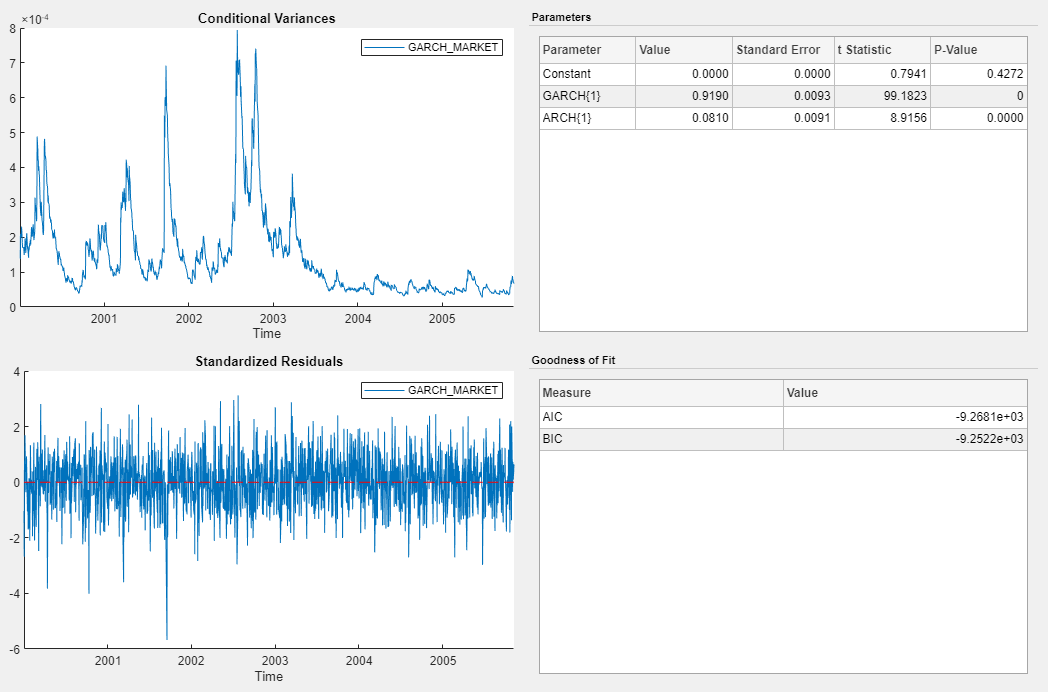
Значения p оценок коэффициентов близки к нулю, что указывает на то, что оценки значительны. Конечные условные отклонения показывают высокую волатильность до 2003 года, затем небольшую волатильность до 2005 года. Стандартизированные невязки, по-видимому, колеблются около y = 0, и существует несколько больших (в величине) невязок.
Оцените, являются ли стандартизированные невязки обычно распределенными и некоррелированными. Затем оцените, имеет ли остаточный ряд затяжную условную гетероскедастичность.
Оцените, распределены ли обычно стандартизированные невязки, путем построения гистограммы и квантильного графика:
На панели Models выберите GARCH_MARKET.
На вкладке Econometric Modeler, в разделе Diagnostics, нажмите Residual Diagnostics > Residual Histogram.
В Diagnostics разделе щелкните Residual Diagnostics > Residual Q-Q Plot.
Гистограмма и квантильный график появляются в Histogram(GARCH_MARKET) и QQPlot(GARCH_MARKET) окнах рисунка, соответственно.
Оцените, являются ли стандартизированные невязки автокоррелированными, путем построения графика их автокорреляционной функции (ACF).
На панели Models выберите GARCH_MARKET.
На вкладке Econometric Modeler, в разделе Diagnostics, нажмите Residual Diagnostics > Autocorrelation Function.
График ACF появляется в ACF(GARCH_MARKET) окне рисунка.
Оцените, имеет ли остаточный ряд затяжную условную гетероскедастичность, путем построения графика ACF квадратов стандартизированных невязок:
На панели Models выберите GARCH_MARKET.
Перейдите на вкладку Econometric Modeler. Затем в разделе Diagnostics щелкните Residual Diagnostics > Squared Residual Autocorrelation.
ACF квадратов стандартизированных невязок появляется в ACF(GARCH_MARKET)2 окне рисунка.
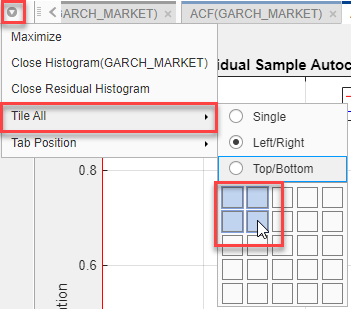
Расположите гистограмму, график квантиль-квантиль, ACF и ACF квадратного стандартизированного остаточного ряда так, чтобы они занимали четыре квадранта правой панели. На панели Documents нажмите кнопку Document Actions, ![]() выберите Tile All, поместите указатель мыши в (2,2) положение матрицы квадратов.
выберите Tile All, поместите указатель мыши в (2,2) положение матрицы квадратов.
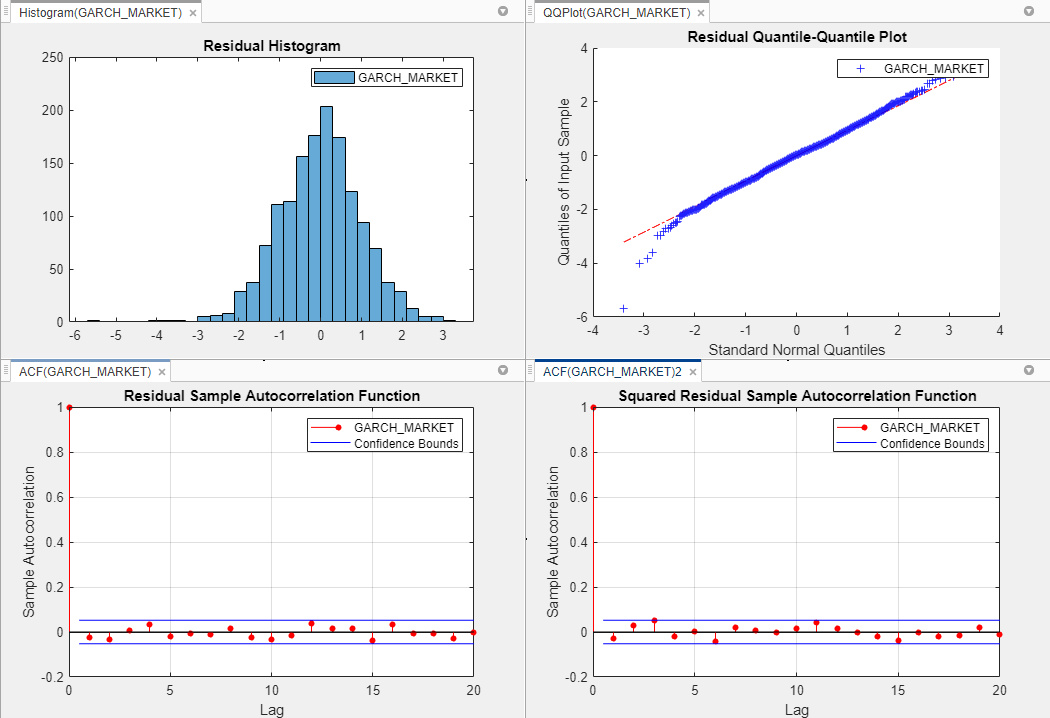
Хотя результаты показывают несколько больших стандартизированные невязки, они, по-видимому, примерно нормально распределены. Графики ACF стандартизированных и квадратов стандартизированных невязок не содержат каких-либо значительных автокорреляций. Поэтому разумно сделать вывод, что стандартизированные невязки являются некоррелированными и гомосцедастическими.