Ценовые свопционы с моделями процентных ставок с использованием симуляции

Введение

В этом примере показано, как оценить европейские свопции с помощью моделей процентных ставок в Financial Instruments Toolbox™. В частности, модель одного фактора Халла-Уайта, модель линейного Гауссова двухфактора и модель рынка LIBOR калибруются к рыночным данным, а затем используются, чтобы сгенерировать пути процентных ставок с помощью симуляции Монте-Карло.

В следующих разделах настраиваются данные, которые затем используются с примерами для моделирования путей процентной ставки с помощью модели одного фактора Халл-Уайт, моделирования путей процентной ставки с помощью линейной Гауссовой двухфакторной модели и моделирования путей процентной ставки с использованием модели рынка LIBOR:

Построение нулевой кривой

Открыть Live Script

В этом примере показано, как использовать ZeroRates для нулевой кривой, которая жестко закодирована. Можно также создать нулевую кривую путем загрузки нулевой кривой из рыночных данных (для примера, депозитов, фьючерсов/форвардов и свопов)

Жестко закодированные данные для нулевой кривой заданы как:

Settle = datenum('21-Jul-2008');

% Zero Curve
CurveDates = daysadd(Settle,360*([1 3 5 7 10 20]),1);
ZeroRates = [1.9 2.6 3.1 3.5 4 4.3]'/100;

plot(CurveDates,ZeroRates)
datetick
title(['Zero Curve for ' datestr(Settle)]);

Figure contains an axes. The axes with title Zero Curve for 21-Jul-2008 contains an object of type line.

Создайте IRCurve объект.

irdc = IRDataCurve('Zero',Settle,CurveDates,ZeroRates);

Создайте RateSpec.

RateSpec = intenvset('Rates',ZeroRates,'EndDates',CurveDates,'StartDate',Settle)

RateSpec = struct with fields:
           FinObj: 'RateSpec'
      Compounding: 2
             Disc: [6x1 double]
            Rates: [6x1 double]
         EndTimes: [6x1 double]
       StartTimes: [6x1 double]
         EndDates: [6x1 double]
       StartDates: 733610
    ValuationDate: 733610
            Basis: 0
     EndMonthRule: 1

Задайте параметры свопцирования

В то время как симуляция Монте-Карло обычно используется, чтобы оценить более сложные производные (например, бермудские свопционы), в этом примере цена европейского свопциона вычисляется с датой исполнения пять лет и базовым свопом пять лет.

InstrumentExerciseDate = datenum('21-Jul-2013');
InstrumentMaturity = datenum('21-Jul-2018');
InstrumentStrike = .045;

Вычислите черную модель и матрицу волатильности Swaption

Модель Black часто используется для ценообразования и котировки европейских опций процентных ставокто есть прописных букв, полов и свопционов. В случае свопционов модель Блэка используется, чтобы подразумевать волатильность, учитывая текущую наблюдаемую рыночную цену. Следующая матрица показывает черную подразумеваемую волатильность для области значений дат упражнений по сваптированию (столбцы) и базовых сроков свопа (строки).

SwaptionBlackVol = [22 21 19 17 15 13 12
    21 19 17 16 15 13 11
    20 18 16 15 14 12 11
    19 17 15 14 13 12 10
    18 16 14 13 12 11 10
    15 14 13 12 12 11 10
    13 13 12 11 11 10 9]/100;
ExerciseDates = [1:5 7 10];
Tenors = [1:5 7 10];

EurExDatesFull = repmat(daysadd(Settle,ExerciseDates*360,1)',...
    length(Tenors),1);
EurMatFull = reshape(daysadd(EurExDatesFull,...
    repmat(360*Tenors,1,length(ExerciseDates)),1),size(EurExDatesFull));

Выбор калибровочных приборов

Выбор приборов для калибровки модели является одной из задач калибровки. Для бермудских свопционов типично калибровать на европейские свопционы, которые являются совместными с бермудским свопционом, которые должны быть оценены. В этом случае в калибровке используются все свопционы, имеющие базовый тенор, который созревает до погашения свопциона, который будет оцениваться (21-Jul-2018).

% Find the swaptions that expire on or before the maturity date of the
% sample swaption
relidx = find(EurMatFull <= InstrumentMaturity);

Вычисление цен на Swaption с использованием модели Black's

В этом примере показано, как вычислить цены свопциона с помощью Модель. Затем цены свопциона используются для сравнения прогнозируемых значений модели, которые получаются в процессе калибровки.

Чтобы вычислить цены свопциона с помощью модели Black's:

SwaptionBlackPrices = zeros(size(SwaptionBlackVol));
SwaptionStrike = zeros(size(SwaptionBlackVol));

for iSwaption=1:length(ExerciseDates)
    for iTenor=1:length(Tenors)
        [~,SwaptionStrike(iTenor,iSwaption)] = swapbyzero(RateSpec,[NaN 0], Settle, EurMatFull(iTenor,iSwaption),...
            'StartDate',EurExDatesFull(iTenor,iSwaption),'LegReset',[1 1]);
        SwaptionBlackPrices(iTenor,iSwaption) = swaptionbyblk(RateSpec, 'call', SwaptionStrike(iTenor,iSwaption),Settle, ...
            EurExDatesFull(iTenor,iSwaption), EurMatFull(iTenor,iSwaption), SwaptionBlackVol(iTenor,iSwaption));
    end
end

Задайте параметры симуляции

В этом примере показано, как использовать simTermStructs метод с HullWhite1F, LinearGaussian2F, и LiborMarketModel объекты.

Чтобы продемонстрировать использование simTermStructs метод с HullWhite1F, LinearGaussian2F, и LiborMarketModel используйте следующие параметры симуляции:

nPeriods = 5;
DeltaTime = 1;
nTrials = 1000;

Tenor = (1:10)';

SimDates = daysadd(Settle,360*DeltaTime*(0:nPeriods),1)
SimTimes = diff(yearfrac(SimDates(1),SimDates))

% For 1 year periods and an evenly spaced tenor, the exercise row will be
% the 5th row and the swaption maturity will be the 5th column
exRow = 5;
endCol = 5;

Симулируйте пути процентной ставки с помощью однофакторной модели корпуса-белого

В этом примере показано, как симулировать пути процентной ставки с помощью модели Hull-White с одним фактором. Прежде чем начать этот пример, который использует HullWhite1F модель, убедитесь, что вы настроили данные, как описано в:

Модель с одним фактором Халла-Уайта описывает эволюцию короткой скорости и задается с помощью параметров нуля, alpha и sigma для уравнения

$d r = [θ (t) - a (t) r] d t + σ (t) d W$

где:

dr - это изменение краткосрочной процентной ставки на небольшом интервале, dt.

r - краткосрочная процентная ставка.

Θ(t) является функцией времени, определяющей среднее направление, в котором r движется, выбранное таким образом, чтобы движения в r соответствовали сегодняшнему кривому нулевому купонному выражению.

α - средняя скорость реверсии.

dt - это небольшое изменение во времени.

σ - ежегодное стандартное отклонение короткой скорости.

W - броуновское движение.

Модель Халла-Уайта калибруется с помощью функции swaptionbyhw, который создает триномиальное дерево, чтобы оценить свопционы. Калибровка состоит из минимизации различия между наблюдаемыми рыночными ценами (вычисленными выше с помощью подразумеваемой матрицы волатильности свопции Black, см. Вычисление черной модели и матрицы волатильности Swaption) и предсказанными ценами модели.

В этом примере функция Optimization Toolbox™ lsqnonlin используется для поиска набора параметров, который минимизирует различие между наблюдаемым и предсказанными значениями. Однако могут быть подходящими и другие подходы (для примера, моделируемого отжига). Стартовые параметры и ограничения для α и σ заданы в переменных x0, lb, и ub; они могут также варьироваться в зависимости от конкретного подхода к калибровке.

Калибруйте набор параметров, которые минимизируют различие между наблюдаемым и предсказанными значениями, используя swaptionbyhw и lsqnonlin.

TimeSpec = hwtimespec(Settle,daysadd(Settle,360*(1:11),1), 2);
HW1Fobjfun = @(x) SwaptionBlackPrices(relidx) - ...
    swaptionbyhw(hwtree(hwvolspec(Settle,'11-Aug-2015',x(2),'11-Aug-2015',x(1)), RateSpec, TimeSpec), 'call', SwaptionStrike(relidx),...
    EurExDatesFull(relidx), 0, EurExDatesFull(relidx), EurMatFull(relidx));
options = optimset('disp','iter','MaxFunEvals',1000,'TolFun',1e-5);

% Find the parameters that minimize the difference between the observed and
% predicted prices
x0 = [.1 .01];
lb = [0 0];
ub = [1 1];
HW1Fparams = lsqnonlin(HW1Fobjfun,x0,lb,ub,options);

HW_alpha = HW1Fparams(1)
HW_sigma = HW1Fparams(2)

                                        Norm of      First-order 
 Iteration  Func-count     f(x)          step          optimality
     0          3        0.953772                          20.5
     1          6        0.142828      0.0169199           1.53
     2          9        0.123022      0.0146705           2.31
     3         12        0.122222      0.0154098          0.482
     4         15        0.122217     0.00131297        0.00409 

Local minimum possible.

lsqnonlin stopped because the final change in the sum of squares relative to 
its initial value is less than the selected value of the function tolerance.

HW_alpha =

    0.0967


HW_sigma =

    0.0088

Создайте HullWhite1F модели с использованием HullWhite1F конструктор.

HW1F = HullWhite1F(RateSpec,HW_alpha,HW_sigma)

HW1F = 

  HullWhite1F with properties:

    ZeroCurve: [1x1 IRDataCurve]
        Alpha: @(t,V)inAlpha
        Sigma: @(t,V)inSigma

Используйте симуляцию Монте-Карло, чтобы сгенерировать пути процентной ставки с HullWhite1F.simTermStructs.

HW1FSimPaths = HW1F.simTermStructs(nPeriods,'NTRIALS',nTrials,...
    'DeltaTime',DeltaTime,'Tenor',Tenor,'antithetic',true);
trialIdx = 1;
figure
surf(Tenor,SimDates,HW1FSimPaths(:,:,trialIdx))
datetick y keepticks keeplimits
title(['Evolution of the Zero Curve for Trial:' num2str(trialIdx) ' of Hull White Model'])
xlabel('Tenor (Years)')

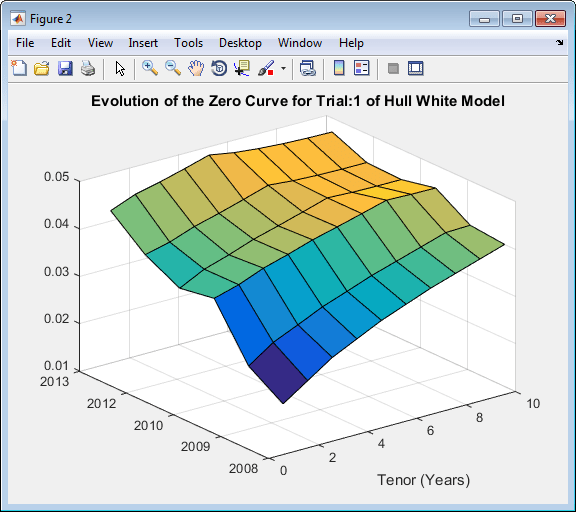
Цена европейского свопциона.

DF = exp(bsxfun(@times,-HW1FSimPaths,repmat(Tenor',[nPeriods+1 1])));
SwapRate = (1 - DF(exRow,endCol,:))./sum(bsxfun(@times,1,DF(exRow,1:endCol,:)));
PayoffValue = 100*max(SwapRate-InstrumentStrike,0).*sum(bsxfun(@times,1,DF(exRow,1:endCol,:)));
RealizedDF = prod(exp(bsxfun(@times,-HW1FSimPaths(1:exRow,1,:),SimTimes(1:exRow))),1);
HW1F_SwaptionPrice = mean(RealizedDF.*PayoffValue)

HW1F_SwaptionPrice =

    2.1839

Симулируйте пути процентной ставки с помощью линейной Гауссовой двухфакторной модели

В этом примере показано, как симулировать пути процентной ставки с помощью двухфакторной модели Линейного Гауссова. Прежде чем начать этот пример, который использует LinearGaussian2F модель, убедитесь, что вы настроили данные, как описано в:

Линейная Гауссова двухфакторная модель (называемая Brigo и Mercurio G2 + +, см. Моделирование процентной ставки с использованием симуляции Монте-Карло) также является короткой тарифной моделью, но включает два фактора. В частности:

$r (t) = x (t) + y (t) + ϕ (t)$

$d x (t) = - a (t) x (t) d t + σ (t) d W_{1} (t), x (0) = 0$

$d y (t) = - b (t) y (t) d t + η (t) d W_{2} (t), y (0) = 0$

где $d W_{1} (t) d W_{2} (t) = ρ d t$ является двумерным броуновским движением с корреляционными ρ, и ϕ является функцией, выбранной так, чтобы соответствовать начальной нулевой кривой.

Функция swaptionbylg2f используется для вычисления аналитических значений цены свопциона для параметров модели, и поэтому может использоваться для калибровки модели. Калибровка состоит из минимизации различия между наблюдаемыми рыночными ценами (вычисленными выше с помощью подразумеваемой матрицы волатильности свопции Black, см. Вычисление черной модели и матрицы волатильности Swaption) и предсказанными ценами модели.

В этом примере подход похож на Моделирование путей процентной ставки с использованием модели Hull-White One-Factor и функции Optimization Toolbox lsqnonlin используется для минимизации различия между наблюдаемыми ценами свопциона и прогнозируемыми ценами свопциона. Однако могут быть подходящими и другие подходы (для примера, моделируемого отжига). Стартовые параметры и ограничения для a, b, η, ρ, и σ установлены в переменных x0, lb, и ub; они могут также варьироваться в зависимости от конкретного подхода к калибровке.

Калибруйте набор параметров, которые минимизируют различие между наблюдаемым и предсказанными значениями, используя swaptionbylg2f и lsqnonlin.

G2PPobjfun = @(x) SwaptionBlackPrices(relidx) - swaptionbylg2f(irdc,x(1),x(2),x(3),x(4),x(5),SwaptionStrike(relidx),...
    EurExDatesFull(relidx),EurMatFull(relidx),'Reset',1);

options = optimset('disp','iter','MaxFunEvals',1000,'TolFun',1e-5);
x0 = [.2 .1 .02 .01 -.5];
lb = [0 0 0 0 -1];
ub = [1 1 1 1 1];
LG2Fparams = lsqnonlin(G2PPobjfun,x0,lb,ub,options)

                                         Norm of      First-order 
 Iteration  Func-count     f(x)          step          optimality
     0          6         12.3547                          67.6
     1         12         1.37984      0.0979743           8.59      
     2         18         1.37984       0.112847           8.59      
     3         24        0.445202      0.0282118           1.31      
     4         30        0.236746      0.0564236           3.02      
     5         36        0.134678      0.0843366           7.78      
     6         42       0.0398816       0.015084           6.34      
     7         48       0.0287731       0.038967          0.732      
     8         54       0.0273025       0.112847          0.881      
     9         60       0.0241689       0.213033           1.06      
    10         66       0.0241689       0.125602           1.06      
    11         72       0.0239103      0.0314005           9.78      
    12         78       0.0234246      0.0286685           1.21      
    13         84       0.0234246      0.0491135           1.21      
    14         90        0.023304      0.0122784           1.67      
    15         96       0.0231931      0.0245568           5.92      
    16        102       0.0230898     0.00785421          0.434      
    17        108       0.0230898      0.0245568          0.434      
    18        114        0.023083     0.00613919          0.255    

Local minimum possible.

lsqnonlin stopped because the final change in the sum of squares relative to 
its initial value is less than the selected value of the function tolerance.

LG2Fparams =

    0.5752    0.1181    0.0146    0.0119   -0.7895

Создайте G2PP объект и использование симуляции Монте-Карло, чтобы сгенерировать пути процентной ставки с LinearGaussian2F.simTermStructs.

LG2f_a = LG2Fparams(1);
LG2f_b = LG2Fparams(2);
LG2f_sigma = LG2Fparams(3);
LG2f_eta = LG2Fparams(4);
LG2f_rho = LG2Fparams(5);

G2PP = LinearGaussian2F(RateSpec,LG2f_a,LG2f_b,LG2f_sigma,LG2f_eta,LG2f_rho);

G2PPSimPaths = G2PP.simTermStructs(nPeriods,'NTRIALS',nTrials,...
    'DeltaTime',DeltaTime,'Tenor',Tenor,'antithetic',true);

trialIdx = 1;
figure
surf(Tenor,SimDates,G2PPSimPaths(:,:,trialIdx))
datetick y keepticks keeplimits
title(['Evolution of the Zero Curve for Trial:' num2str(trialIdx) ' of G2++ Model'])
xlabel('Tenor (Years)')

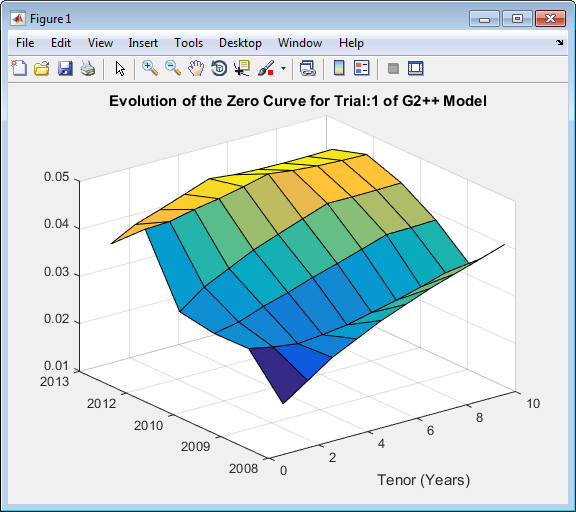
Цена европейского свопциона.

DF = exp(bsxfun(@times,-G2PPSimPaths,repmat(Tenor',[nPeriods+1 1])));
SwapRate = (1 - DF(exRow,endCol,:))./sum(bsxfun(@times,1,DF(exRow,1:endCol,:)));
PayoffValue = 100*max(SwapRate-InstrumentStrike,0).*sum(bsxfun(@times,1,DF(exRow,1:endCol,:)));
RealizedDF = prod(exp(bsxfun(@times,-G2PPSimPaths(1:exRow,1,:),SimTimes(1:exRow))),1);
G2PP_SwaptionPrice = mean(RealizedDF.*PayoffValue)

G2PP_SwaptionPrice =

    2.0988

Симулируйте пути процентной ставки с помощью модели рынка LIBOR

В этом примере показано, как симулировать пути процентных ставок с помощью рыночной модели LIBOR. Прежде чем начать этот пример, который использует LiborMarketModel, убедитесь, что вы настроили данные, как описано в:

Модель рынка LIBOR (LMM) отличается от моделей с короткой ставкой тем, что она развивает набор дискретных форвардных ставок. В частности, lognormal LMM задает следующее диффузионное уравнение для каждой прямой скорости

$\frac{d F_{i} (t)}{F_{i}} = - μ_{i} d t + σ_{i} (t) d W_{i}$

где:

W является N-мерным геометрическим броуновским движением с

$d W_{i} (t) d W_{j} (t) = ρ_{i j}$

LMM связывает дрейфы форвардных скоростей на основе аргументов без арбитража. В частности, под мерой Spot LIBOR, дрейфы выражаются как

$μ_{i} (t) = - σ_{i} (t) \sum_{j = q (t)}^{i} \frac{τ_{j} ρ_{i, j} σ_{j} (t) F_{j} (t)}{1 + τ_{j} F_{j} (t)}$

где:

$τ_{i}$ - временная дробь, связанная с i-й прямой скоростью

q(t) является индексом, заданным отношением

$T_{q (t) - 1} < t < T_{q (t)}$

и числитель Spot LIBOR определяется как

$B (t) = P (t, T_{q (t)}) \prod_{n = 0}^{q (t) - 1} (1 + τ_{n} F_{n} (T_{n}))$

Выбор с LMM - это как смоделировать волатильность и корреляцию и как оценить параметры этих моделей для волатильности и корреляции. На практике можно использовать комбинацию исторических данных (для примера, наблюдаемой корреляции между форвардными ставками) и текущих рыночных данных. В данном примере используются только данные свопциона. Кроме того, существует много различных параметризаций волатильности и корреляции. В этом примере используются две относительно простые параметризации.

Одна из самых популярных функциональных форм в литературе по волатильности:

$σ_{i} (t) = φ_{i} (a (T_{i} - t) + b) e^{c (T_{i} - t)} + d$

где ϕ корректирует кривую, чтобы соответствовать волатильности для i-й скорости передачи. В этом примере все ϕ приняты за 1. Для корреляции используется следующая функциональная форма:

$ρ_{i, j} = e^{- β | i - j |}$

После определения функциональных форм эти параметры должны быть оценены с помощью рыночных данных. Одним из полезных приближений, первоначально разработанных Ребонато, является следующее, которое связывает Чёрную волатильность для европейского свопциона, учитывая набор функций волатильности и матрицу корреляции

${(υ_{_{α, β}}^{L F M})}^{2} = \sum_{i, j = α + 1}^{β} \frac{w_{i} (0) w_{j} (0) F_{i} (0) F_{j} (0) ρ_{i, j}}{S_{α, β} {(0)}^{2}} \int_{0}^{T_{α}} σ_{i} (t) σ_{j} (t) d t$

где:

$w_{i} (t) = \frac{τ_{i} P (t, T_{i})}{\sum_{k = α + 1}^{β} τ_{κ} P (t, t_{κ})}$

Это вычисление выполняется с помощью функции blackvolbyrebonato для вычисления аналитических значений цены свопциона для параметров модели, и, следовательно, затем используется для калибровки модели. Калибровка состоит из минимизации различия между наблюдаемыми подразумеваемыми летучими состояниями черного и предсказанными леткостями черного.

В этом примере подход аналогичен Моделированию путей процентной ставки с использованием модели одного фактора Халл-Уайт и Моделированию путей процентной ставки с помощью линейной Гауссовой двухфакторной модели, где функция Optimization Toolbox lsqnonlin используется для минимизации различия между наблюдаемыми ценами свопциона и прогнозируемыми ценами свопциона. Однако могут быть подходящими и другие подходы (для примера, моделируемого отжига). Стартовые параметры и ограничения для a, b, d и β заданы в переменных x0, lb, и ub; они могут также варьироваться в зависимости от конкретного подхода к калибровке.

Калибруйте набор параметров, которые минимизируют различие между наблюдаемым и предсказанными значениями, используя blackvolbyrebonato и lsqnonlin.

nRates = 10;

CorrFunc = @(i,j,Beta) exp(-Beta*abs(i-j));

objfun = @(x) SwaptionBlackVol(relidx) - blackvolbyrebonato(RateSpec,...
    repmat({@(t) ones(size(t)).*(x(1)*t + x(2)).*exp(-x(3)*t) + x(4)},nRates-1,1),...
    CorrFunc(meshgrid(1:nRates-1)',meshgrid(1:nRates-1),x(5)),...
    EurExDatesFull(relidx),EurMatFull(relidx),'Period',1);

options = optimset('disp','iter','MaxFunEvals',1000,'TolFun',1e-5);

x0 = [.2 .05 1 .05 .2];
lb = [0 0 .5 0 .01];
ub = [1 1 2 .3 1];
LMMparams = lsqnonlin(objfun,x0,lb,ub,options)

                                        Norm of      First-order 
 Iteration  Func-count     f(x)          step          optimality
     0          6        0.156251                         0.483
     1         12      0.00870177       0.188164         0.0339      
     2         18      0.00463441       0.165527        0.00095      
     3         24      0.00331055       0.351017         0.0154      
     4         30      0.00294775      0.0892617       7.47e-05      
     5         36      0.00281565       0.385779        0.00917      
     6         42      0.00278988      0.0145632       4.15e-05      
     7         48      0.00278522       0.115042        0.00116    
Local minimum possible.

lsqnonlin stopped because the final change in the sum of squares relative to 
its initial value is less than the selected value of the function tolerance.

LMMparams =

    0.0781    0.1656    0.5121    0.0617    0.0100

Вычислите VolFunc для LMM объект.

a = LMMparams(1);
b = LMMparams(2);
c = LMMparams(3);
d = LMMparams(4);

Beta = LMMparams(5);

VolFunc = repmat({@(t) ones(size(t)).*(a*t + b).*exp(-c*t) + d},nRates-1,1);

Постройте график функции волатильности.

figure
fplot(VolFunc{1},[0 20])
title('Volatility Function')

CorrelationMatrix = CorrFunc(meshgrid(1:nRates-1)',meshgrid(1:nRates-1),Beta);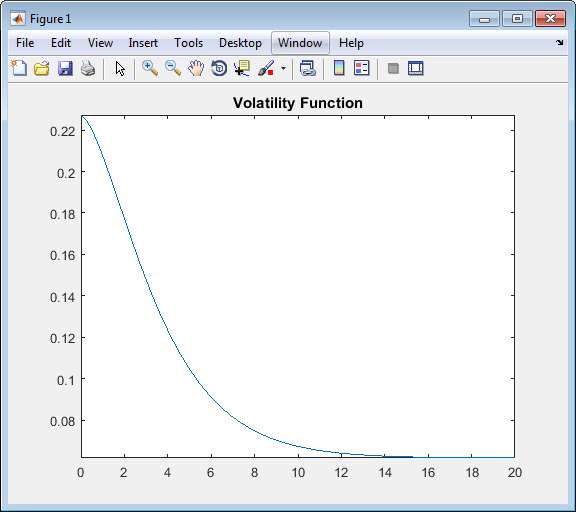

Смотрите матрицу корреляции.

disp('Correlation Matrix')
fprintf([repmat('%1.3f ',1,length(CorrelationMatrix)) ' \n'],CorrelationMatrix)

Correlation Matrix
1.000 0.990 0.980 0.970 0.961 0.951 0.942 0.932 0.923  
0.990 1.000 0.990 0.980 0.970 0.961 0.951 0.942 0.932  
0.980 0.990 1.000 0.990 0.980 0.970 0.961 0.951 0.942  
0.970 0.980 0.990 1.000 0.990 0.980 0.970 0.961 0.951  
0.961 0.970 0.980 0.990 1.000 0.990 0.980 0.970 0.961  
0.951 0.961 0.970 0.980 0.990 1.000 0.990 0.980 0.970  
0.942 0.951 0.961 0.970 0.980 0.990 1.000 0.990 0.980  
0.932 0.942 0.951 0.961 0.970 0.980 0.990 1.000 0.990  
0.923 0.932 0.942 0.951 0.961 0.970 0.980 0.990 1.000

Создайте LMM объект и использование симуляции Монте-Карло, чтобы сгенерировать пути процентной ставки с LiborMarketModel.simTermStructs.

LMM = LiborMarketModel(irdc,VolFunc,CorrelationMatrix,'Period',1);

[LMMZeroRates, ForwardRates] = LMM.simTermStructs(nPeriods,'nTrials',nTrials);

trialIdx = 1;
figure
tmpPlotData = LMMZeroRates(:,:,trialIdx);
tmpPlotData(tmpPlotData == 0) = NaN;
surf(Tenor,SimDates,tmpPlotData)
title(['Evolution of the Zero Curve for Trial:' num2str(trialIdx) ' of LIBOR Market Model'])
xlabel('Tenor (Years)')

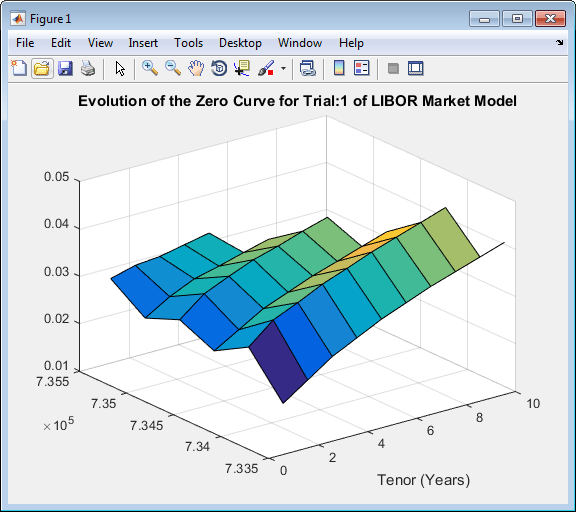
Цена европейского свопциона.

DF = exp(bsxfun(@times,-LMMZeroRates,repmat(Tenor',[nPeriods+1 1])));
SwapRate = (1 - DF(exRow,endCol,:))./sum(bsxfun(@times,1,DF(exRow,1:endCol,:)));
PayoffValue = 100*max(SwapRate-InstrumentStrike,0).*sum(bsxfun(@times,1,DF(exRow,1:endCol,:)));
RealizedDF = prod(exp(bsxfun(@times,-LMMZeroRates(2:exRow+1,1,:),SimTimes(1:exRow))),1);
LMM_SwaptionPrice = mean(RealizedDF.*PayoffValue)

LMM_SwaptionPrice =

    1.9915

Сравнение результатов моделирования процентных ставок

В этом примере показано, как сравнить результаты для ценообразования европейского свопциона с различными моделями процентных ставок.

Сравните результаты для ценообразования европейского свопциона с моделями процентных ставок с помощью симуляции Монте-Карло.

disp(' ')
fprintf('     # of Monte Carlo Trials: %8d\n'    , nTrials)
fprintf('     # of Time Periods/Trial: %8d\n\n'  , nPeriods)
fprintf('HW1F European Swaption Price: %8.4f\n', HW1F_SwaptionPrice)
fprintf('LG2F Europesn Swaption Price: %8.4f\n', G2PP_SwaptionPrice)
fprintf(' LMM European Swaption Price: %8.4f\n', LMM_SwaptionPrice)

 # of Monte Carlo Trials:     1000
     # of Time Periods/Trial:        5

HW1F European Swaption Price:   2.1839
LG2F Europesn Swaption Price:   2.0988
 LMM European Swaption Price:   1.9915

Ссылки

Brigo, D. and F. Mercurio, модели процентных ставок - теория и практика с улыбкой, инфляция и кредит, Springer Finance, 2006.

Андерсен, Л. и В. Питербарг, моделирование процентных ставок, Atlantic Financial Press. 2010.

Hull, J, опции, Futures, and Other Derivatives, Springer Finance, 2003.

Glasserman, P, Monte Carlo Methods in Financial Engineering, Prentice Hall, 2008.

Rebonato, R., K. McKay, and R. White, The Sabr/Libor Market Model: ценообразование, калибровка и хеджирование для сложных производных по процентным ставкам, John Wiley & Sons, 2010.

См. также

Документация