Сетчатые данные состоят из значений или измерений в регулярно разнесенных точках, которые образуют сетку. Данные с сеткой возникают во многих областях, таких как метеорология, обследование и медицинская визуализация. В этих областях обычно проводят измерения с регулярными пространственными интервалами, возможно, с течением времени. Эти упорядоченные сетки данных могут варьироваться от 1-D (для простых временных рядов) до 4-D (для измерения объемов с течением времени) или выше. Некоторые примеры данных с сеткой:
1-D: Цены акций с течением времени
2-D: Температура поверхности
3-D: МРТ- изображение головного мозга
4-D: Измерения океана в объеме воды с течением времени
Во всех этих приложениях основанная на сетке интерполяция эффективно распространяет полезность данных на точки, где не было проведено измерений. Для примера, если у вас есть почасовые данные цены для запаса, можно использовать интерполяцию, чтобы аппроксимировать цену каждые 15 минуты.
MATLAB® предоставляет несколько инструментов для интерполяции на основе сетки:
meshgrid и ndgrid функции создают сетки различной размерности. meshgrid может создавать 2-D или 3-D сетки, в то время как ndgrid может создавать сетки с любым количеством размерностей. Эти функции возвращают сетки с различными форматами выхода. Преобразовать между этими форматами сетки можно используя pagetranspose (начиная с R2020b) или permute функции для замены первых двух размерностей сетки.
The interp семейство функций включает interp1, interp2, interp3, и interpn. Каждая функция предназначена для интерполяции данных с определенным количеством размерностей. interp2 и interp3 использовать сетки в meshgrid формат, в то время как interpn использует сетки в ndgrid формат.
griddedInterpolant объекты поддерживают интерполяцию в любом количестве размерностей для данных в ndgrid формат. Эти объекты также поддерживают многозначную интерполяцию (начиная с R2021a), где каждая точка сетки может иметь несколько значений, связанных с ней.
Существуют преимущества памяти и эффективности при использовании griddedInterpolant объекты по interp функций. griddedInterpolant предлагает существенные улучшения эффективности для повторных запросов интерполяционного объекта, в то время как interp функции выполняют новое вычисление каждый раз, когда они вызываются. Кроме того, griddedInterpolant сохраняет точки выборки в эффективном для памяти формате (как компактную сетку) и многопоточно, чтобы использовать преимущества многоядерного компьютера процессоров.
MATLAB позволяет представлять сетку в одном из трех представлений: полной сетки, компактной сетки или сетки по умолчанию. Сетка по умолчанию и компактная сетка используются в основном для удобства и повышения эффективности, соответственно.
full grid является такой, в которой все точки определены явно. Выходные выходы ndgrid и meshgrid задайте полную сетку. Можно создать полные uniform сетки, в которых точки в каждой размерности имеют равные интервалы, или nonuniform, в которых интервалы изменяются в одних или нескольких размерностях. Равномерные сетки могут иметь различные интервалы в каждой размерности, пока интервалы постоянны в каждой размерности.
| Униформа | Униформа | Неоднородный |
|---|---|---|
|
|
|
Примером однородной полной сетки является:
[X,Y] = meshgrid([1 2 3],[3 6 9 12])
X =
1 2 3
1 2 3
1 2 3
1 2 3
Y =
3 3 3
6 6 6
9 9 9
12 12 12Явное определение каждой точки в сетке может потреблять много памяти, когда вы имеете дело с большими сетками. Представление compact grid является способом обойтись без служебных данных памяти полной сетки. Компактное представление сетки сохраняет только grid vectors (по одному для каждой размерности) вместо полной сетки. Вместе векторы сетки неявно определяют сетку. Фактически, входы для meshgrid и ndgrid являются векторами сетки, и эти функции реплицируют векторы сетки, формируя полную сетку. Компактное представление сетки позволяет вам обойти создание сетки и предоставить векторы сетки непосредственно в функцию интерполяции.
Для примера рассмотрим два вектора, x1 = 1:3 и x2 = 1:5. Можно думать об этих векторах как о наборе координат в x1 направление и набор координат в x2 направление, как так:
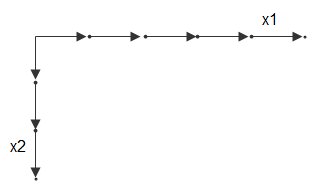
Каждая стрела указывает на местоположение. Можно использовать эти два вектора, чтобы задать набор точек сетки, где один набор координат задается x1 а другой набор координат задается x2. Когда векторы сетки реплицируются, они образуют два массива координат, которые составляют полную сетку:
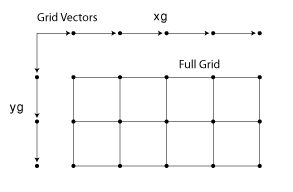
Ваши входные векторы сетки могут быть monotonic или nonmonotonic. Монотонные векторы содержат значения, которые либо увеличиваются в этой размерности, либо уменьшаются в этой размерности. И наоборот, немонотонные векторы содержат значения, которые колеблются. Если входной вектор сетки немонотонен, например [2 4 6 3 1], затем [X1,X2] = ndgrid([2 4 6 3 1]) выводит немонотонную сетку. Ваши векторы сетки должны быть монотонными, если вы намерены передать сетку другим функциям MATLAB. sort функция полезна для обеспечения монотонности.
В некоторых приложениях важны только значения в точках сетки, а не расстояния между точками сетки. Для примера большинство МРТ сканов собирать данные, которые равномерно распределены во всех направлениях. В подобных случаях можно разрешить функции интерполяции автоматически генерировать представление default grid для использования с данными. Для этого оставьте входные входы сетки в функции интерполяции. Когда вы исключаете входы сетки, функция автоматически рассматривает данные как находящиеся на сетке с единичными интервалами. Функция создает сетку с единичными интервалами во время ее выполнения, спасая вас от проблемы создания сетки самостоятельно.
Рассмотрим данные о температуре, собранные на поверхности с регулярными интервалами 5 см, простирающимися на 20 см в каждом направлении. Использовать meshgrid для создания полной сетки.
[X,Y] = meshgrid(0:5:20)
X =
0 5 10 15 20
0 5 10 15 20
0 5 10 15 20
0 5 10 15 20
0 5 10 15 20
Y =
0 0 0 0 0
5 5 5 5 5
10 10 10 10 10
15 15 15 15 15
20 20 20 20 20Координаты (x, y) каждой точки сетки представлены как соответствующие элементы в X и Y матрицы. Первая точка сетки задается как [X(1) Y(1)], что [0 0]следующая точка сетки определяется [X(2) Y(2)], что [0 5]и так далее.
Теперь создайте матрицу, чтобы представлять измерения температуры на сетке, а затем постройте график данных как поверхности.
T = [1 1 10 1 1;
1 10 10 10 10;
100 100 1000 100 100;
10 10 10 10 1;
1 1 10 1 1];
surf(X,Y,T)
view(2)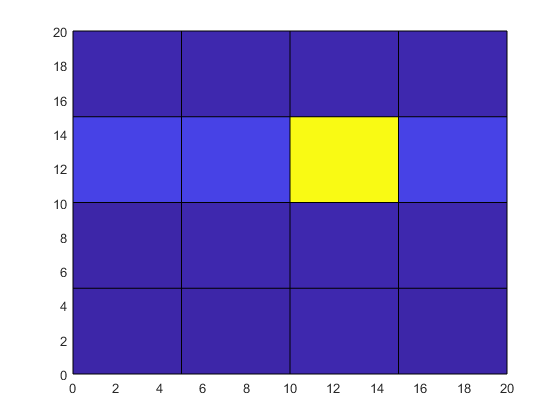
Хотя температура в центральной точке сетки большая, ее расположение и влияние на окружающие точки сетки не очевидны из необработанных данных.
Чтобы улучшить разрешение данных в 10 раз, используйте interp2 чтобы интерполировать данные о температуре в более мелкую сетку, которая использует интервалы 0,5 см. Использовать meshgrid снова, чтобы создать более мелкую сетку, представленную матрицами Xq и Yq. Затем используйте interp2 с исходной сеткой, данными о температуре и новыми точками сетки и постройте график получившихся данных. По умолчанию, interp2 использует линейную интерполяцию в каждой размерности.
[Xq,Yq] = meshgrid(0:0.5:20); Tq = interp2(X,Y,T,Xq,Yq); surf(Xq,Yq,Tq) view(2)
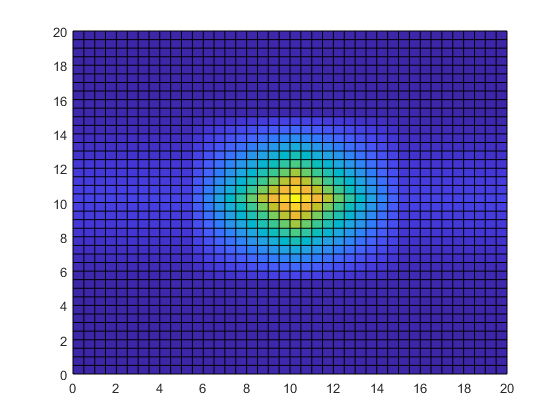
Интерполяция данных о температуре добавляет детализацию изображению и значительно улучшает полезность данных в области измерений.
Основанные на сетке функции интерполяции и объекты в MATLAB предлагают несколько различных методов интерполяции. При выборе метода интерполяции имейте в виду, что некоторым требуется больше памяти или больше времени расчетов, чем другим. Вы, возможно, должны будете обменяться этими ресурсами, чтобы достичь желаемой плавности в результате. В следующей таблице дается предварительный просмотр каждого метода интерполяции, применяемого к одним и тем же 1-D данным, а также дается обзор преимуществ, компромиссов и требований для каждого метода.
| Метод | Описание |
|---|---|
|
| Интерполированное значение в точке запроса является значением в ближайшей точке сетки расчета.
|
|
| Интерполированное значение в точке запроса является значением в следующей точке сетки расчета.
|
|
| Интерполированное значение в точке запроса является значением в предыдущей точке сетки образца.
|
|
| Интерполированное значение в точке запроса основано на линейной интерполяции значений в соседних точках сетки в каждой соответствующей размерности.
|
|
| Интерполированное значение в точке запроса основано на сохраняющей форму кусочно-кубической интерполяции значений в соседних точках сетки.
|
|
| Интерполированное значение в точке запроса основано на кубической интерполяции значений в соседних точках сетки в каждой соответствующей размерности.
|
|
| Интерполированное значение в точке запроса основано на кусочно-линейной функции полиномов со степенью не более трех, оцененных с использованием значений соседних точек сетки в каждой соответствующей размерности. Формула Акимы изменена, чтобы избежать перерегулирования.
|
|
| Интерполированное значение в точке запроса основано на кубической интерполяции значений в соседних точках сетки в каждой соответствующей размерности.
|
griddedInterpolant | interp1 | interp2 | interp3 | interpn