Интерпретация H-бесконечной нормы

Нормы сигналов и систем

Существует несколько способов определения норм скалярного сигнала e (t) во временном интервале. Мы часто будем использовать 2-норму, (_L 2-норму), для математического удобства, которая определяется как

${‖ e ‖}_{2} : = {(\int_{- \infty}^{\infty} e {(t)}^{2} d t)}^{\frac{1}{2}} .$

Если этот интеграл конечен, то сигнал e является квадратным интегрируемым, обозначаемым как e ∊ _L2. Для векторных сигналов

$e (t) = [\begin{matrix} e_{1} (t) \\ e_{2} (t) \\ ⋮ \\ e_{n} (t) \end{matrix}],$

2-норма определяется как

$\begin{matrix} {‖ e ‖}_{2} : = {(\int_{- \infty}^{\infty} {‖ e (t) ‖}_{2}^{2} d t)}^{\frac{1}{2}} \\ = {(\int_{- \infty}^{\infty} e^{T} (t) e (t) d t)}^{\frac{1}{2}} . \end{matrix}$

В ,-инструментах динамические системы, с которыми мы имеем дело, являются исключительно линейными, с моделью пространства состояний

$[\begin{matrix} \dot{x} \\ e \end{matrix}] = [\begin{matrix} A & B \\ C & D \end{matrix}] [\begin{matrix} x \\ d \end{matrix}],$

или, в форме передаточной функции,

e (s) = T (s) d (s), T (s): = C (sI-A)^–1B + D

Две математически удобные меры передаточной матрицы T (s) в частотный диапазон являются матричными _H2 и _H∞ нормами,

$\begin{array}{l} {‖ T ‖}_{2} : = {[\frac{1}{2 π} \int_{- \infty}^{\infty} {‖ T (j ω) ‖}_{F}^{2} d ω]}^{\frac{1}{2}} \\ {‖ T ‖}_{\infty} : = \underset{ω \in R}{\max \bar{σ}} [T (j ω)], \end{array}$

где норма Фробениуса (см. MATLAB^® norm команда) комплексной матрицы M есть

${‖ M ‖}_{F} : = \sqrt{Trace (M^{*} M)} .$

Обе эти нормы передаточной функции имеют интерпретации во временной области ввода/вывода. Если, начиная с начального условия x (0) = 0, два сигнала d и e связаны между

$[\begin{matrix} \dot{x} \\ e \end{matrix}] = [\begin{matrix} A & B \\ C & D \end{matrix}] [\begin{matrix} x \\ d \end{matrix}],$

тогда

Для d, интенсивности модулей, процесса белого шума, установившееся отклонение e равно ∥ T ∥ 2.
Коэффициент усиления L 2 (или RMS) от d → e,
$\max_{d \neq 0} \frac{{‖ e ‖}_{2}}{{‖ d ‖}_{2}}$
равно ∥ T ∥∞. Это более подробно рассмотрено в следующем разделе.

Использование взвешенных норм для характеристики эффективности

Любой критерий эффективности должен также учитываться

Относительная величина внешних воздействий
Частотная зависимость сигналов
Относительная важность величин регулируемых переменных

Таким образом, если цель эффективности находится в форме матричной нормы, это должна быть фактически взвешенная норма

∥ ∥ WLTWR

где матрицы весовых функций _WL и _WR являются частотно-зависимыми, для расчета ограничений полосы пропускания и спектрального содержимого экзогенных сигналов. Самый естественный (математический) способ характеристики приемлемой эффективности - с точки зрения нормы MIMO ∥· _∥∞ (_H∞). По этой причине в настоящем разделе рассматриваются некоторые толкования _H∞ нормы.

Невзвешенная система MIMO

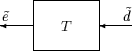
Предположим, T является стабильной линейной системой MIMO с матрицей передаточных функций T (s). Для заданного ведущего сигнала $\tilde{d} (t)$ , задайте $\tilde{e}$ как выход, как показано ниже.

Обратите внимание, что более традиционно записывать схему в невзвешенной системе MIMO: Векторы слева направо со стрелами слева направо, как в взвешенной системе MIMO.

Невзвешенная система MIMO: векторы слева направо

Две схемы, показанные выше, представляют точно такую же систему. Мы предпочитаем записывать эти блоки со стрелами, идущими вправо налево, чтобы соответствовать матрице и составу оператора.

Предположим, что размерности T являются _ne × _nd. Предположим, β > 0 будет определено как

$β : = {‖ T ‖}_{\infty} : = \underset{ω \in R}{\max \bar{σ} [T (j ω)]} .$

Теперь рассмотрим ответ, начиная с начального условия, равного 0. В этом случае теорема Парсеваля дает, что

$\frac{{‖ \tilde{e} ‖}_{2}}{{‖ \tilde{d} ‖}_{2}} = \frac{{[\int_{0}^{\infty} {\tilde{e}}^{T} (t) \tilde{e} (t) d t]}^{\frac{1}{2}}}{{[\int_{0}^{\infty} {\tilde{d}}^{T} (t) \tilde{d} (t) d t]}^{\frac{1}{2}}} \leq β .$

Кроме того, существуют определенные нарушения порядка d, которые приводят к отношению ${‖ \tilde{e} ‖}_{2} / {‖ \tilde{d} ‖}_{2}$ произвольно близок к β. Из- ∥ этого T ∥∞ упоминается как коэффициент усиления L 2 (или RMS) системы.

Как вы ожидаете, синусоидальная, установившаяся интерпретация ∥ T ∥∞ также возможна: Для любой частоты $\bar{ω} \in R$ , любой вектор амплитуд $a \in R_{n_{d}}$ , и любой вектор фаз $ϕ \in R^{n_{d}}$ с помощью ∥ a ∥ 2 ≤ 1 задайте сигнал времени

$\tilde{d} (t) = [\begin{matrix} a_{1} \sin (\bar{ω} t + ϕ_{1}) \\ ⋮ \\ a_{n_{d}} \sin (\bar{ω} t + ϕ_{n_{d}}) \end{matrix}] .$

Применение этого входа к системе T приводит к установившейся реакции ${\tilde{e}}_{s s}$ формы

${\tilde{e}}_{s s} (t) = [\begin{matrix} b_{1} \sin (\bar{ω} t + ϕ_{1}) \\ ⋮ \\ b_{n_{e}} \sin (\bar{ω} t + ϕ_{n_{e}}) \end{matrix}] .$

Вектор $b \in R^{n_{e}}$ удовлетворяет ∥ b ∥ 2 ≤ β. Более того, β, как определено в Взвешенной Системе MIMO, является наименьшим числом, таким что это верно для каждого _∥ a ∥ 2 ≤ 1, $\bar{ω}$ , и ϕ.

Обратите внимание, что в этой интерпретации векторы синусоидальных величин реакций невзвешены и измерены в евклидовой норме. Если реалистичные многопараметрические цели эффективности должны быть представлены одной целью MIMO ∥· _∥∞ на передаточной функции с обратной связью, необходимы дополнительные масштабирования. Поскольку многие различные цели объединяются в одну матрицу, и связанные с ними затраты являются нормой матрицы, важно использовать частотно-зависимые функции взвешивания, чтобы различные требования могли быть содержательно объединены в одну функцию затрат. Наиболее легко интерпретировать диагональные веса.

Рассмотрим схему Взвешенной Системы MIMO, наряду с Невзвешенной Системой MIMO: Векторы слева направо.

Предположим, что _WL и _WR являются диагональными, стабильными матрицами передаточных функций с диагональными элементами, обозначенными _Li и _Ri.

$W_{L} = [\begin{matrix} L_{1} & 0 & \dots & 0 \\ 0 & L_{2} & \dots & 0 \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & \dots & L_{n_{e}} \end{matrix}], W_{R} = [\begin{matrix} R_{1} & 0 & \dots & 0 \\ 0 & R_{2} & \dots & 0 \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & \dots & R_{n_{d}} \end{matrix}] .$

Взвешенная система MIMO

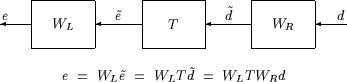
Ограничения, накладываемые на ∥ _WLTWR ∥∞, будут подразумевать ограничения, накладываемые на синусоидальное статическое поведение сигналов $\tilde{d}$ и $\tilde{e} (= T \tilde{d})$ в схеме невзвешенной системы MIMO: векторы слева направо. В частности, для синусоидального сигнала $\tilde{d}$ , установившееся соотношение между $\tilde{e} (= T \tilde{d})$ , $\tilde{d}$ и ∥ _WLTWR ∥∞ следующим образом. Установившееся решение ${\tilde{e}}_{s s}$ , обозначаемый как

{\tilde{e}}_{s s} (t) = [\begin{matrix} {\tilde{e}}_{1} \sin (\bar{ω} t + ϕ_{1}) \\ ⋮ \\ {\tilde{e}}_{n_{e}} \sin (\bar{ω} t + ϕ_{n_{d}}) \end{matrix}]

(1)

удовлетворяет

$\sum_{i = 1}^{n_{e}} {| W_{L_{i}} (j \bar{ω}) {\tilde{e}}_{i} |}^{2} \leq 1$

для всех синусоидальных входных сигналов $\tilde{d}$ формы

\tilde{d} (t) = [\begin{matrix} {\tilde{d}}_{1} \sin (\bar{ω} t + ϕ_{1}) \\ ⋮ \\ {\tilde{d}}_{n_{e}} \sin (\bar{ω} t + ϕ_{n_{d}}) \end{matrix}]

(2)

удовлетворение

$\sum_{i = 1}^{n_{d}} \frac{{| {\tilde{d}}_{i} |}^{2}}{{| W_{R_{i}} (j \bar{ω}) |}^{2}} \leq 1$

если и только если ∥ _WLTWR ∥∞ ≤ 1.

Это приблизительно (очень приблизительно - следующий оператор на самом деле не верен) подразумевает, что ∥ _WLTWR ∥∞ ≤ 1 тогда и только тогда, когда для каждой фиксированной частоты $\bar{ω}$ и все синусоидальные нарушения порядка $\tilde{d}$ вида Уравнение 2 удовлетворяющее

$| {\tilde{d}}_{i} | \leq | W_{R_{i}} (j \bar{ω}) |$

установившиеся компоненты ошибки будут удовлетворять

$| {\tilde{e}}_{i} | \leq \frac{1}{| W_{L_{i}} (j \bar{ω}) |} .$

Это показывает, как можно было выбрать веса эффективности, чтобы отразить желаемую частотно-зависимую цель эффективности. Используйте _WR, чтобы представлять относительную амплитуду синусоидов нарушений порядка, которые могут присутствовать, и используйте 1/ _WL, чтобы представлять желаемую верхнюю границу от последующих ошибок, которые генерируются .

Однако помните, что взвешенная норма H∞ на самом деле не дает элементарные ограничения компонентам $\tilde{e}$ на основе элементных границ компонентов $\tilde{d}$ . Точная граница, которую он дает, с точки зрения евклидовых норм компонентов $\tilde{e}$ и $\tilde{d}$ (взвешивается соответственно _WL (j $\bar{ω}$ ) и _WR (j $\bar{ω}$ )).

См. также

hinfstruct | hinfsyn

Документация