H ∞ настройка контроллеров с фиксированной структурой
hinfstruct команда расширяет классический синтез H ∞ ( см.hinfsyn) к системам управления с фиксированной структурой. Если вы незнакомы с построением утяжеляющих функций для захвата проектных требований к синтезу H ∞, используйте systune или looptune вместо этого.
CL = hinfstruct(CL0)genss модели CL0. Эта настройка минимизирует H ∞ норму передаточной функции с обратной связью, смоделированной CL0. Модель CL0 представляет систему управления с обратной связью, которая включает настраиваемые компоненты, такие как контроллеры или фильтры. CL0 могут также включать функции взвешивания, которые захватывают требования проекта.
[ настраивает блоки параметрических контроллеров C,gamma,info]
= hinfstruct(P,C0,options)C0. Эта настройка минимизирует H ∞ норму системы с обратной связью CL0 = lft(P,C0). Чтобы использовать этот синтаксис, выразите свою систему управления и требования к проектированию как модель Standard Form, как на следующем рисунке.
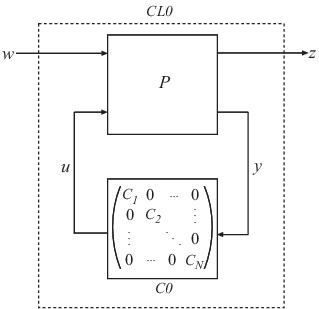
P является числовой моделью LTI, которая включает фиксированные элементы архитектуры управления. P могут также включать функции взвешивания, которые захватывают требования проекта. C0 может быть одним настраиваемым компонентом (для примера, Система управления Блока или genss модель) или массив ячеек из нескольких настраиваемых компонентов. C является параметрической моделью или массивом ячеек параметрических моделей того же типа или типов, как C0.
hinfstruct связана с hinfsyn, который также использует H ∞ методы для разработки контроллера для объекта MIMO. Однако в отличие отhinfstruct, hinfsyn не накладывает ограничения на структуру и порядок контроллера. По этой причине, hinfsyn всегда возвращает меньшее gamma чем hinfstruct. Поэтому можно использовать hinfsyn получить нижнюю границу наилучшей достижимой эффективности.
Используя hinfstruct требует некоторого знакомства с H методами ∞. Необходимо выразить требования проект как функции взвешивания частот на входах и выходах объекта, как описано в Формулировании требований к проектированию как ограничения H-Infinity. Для более простого подхода к настройке фиксированной структуры используйтеsystune или looptune.
hinfstruct использует специализированные методы нескончаемой оптимизации для обеспечения устойчивости замкнутой системы и минимизации H нормы ∞ как функции настраиваемых параметров. Эти методы основаны на работе в [1].
hinfstruct вычисляет норму H∞ с помощью алгоритма [2] и сохраняющих структуру собственных преобразователей из библиотеки SLICOT. Дополнительные сведения о библиотеке SLICOT см. в разделе http://slicot.org.
[1] Apkarian, Pierre, and Dominikus Noll. Nonsmooth H∞ Synthesis (неопр.) (недоступная ссылка). Транзакции IEEE по автоматическому контролю, 51, № 1 (январь 2006 года): 71-86. https://doi.org/10.1109/TAC.2005.860290.
[2] Bruinsma, N. A., and Maarten Steinbuch. «Быстрый алгоритм вычисления H∞-Norm матрицы передаточных функций». Система управления Букв, 14, № 4 (1 апреля 1990): 287-93. https://doi.org/10.1016/0167-6911 (90) 90049-Z .
genss | getValue | hinfstructOptions | hinfsyn | looptune | systune