Количество robust H∞ performance определяет, как смоделированная неопределенность влияет на эффективность цикла обратной связи. Эффективность здесь измеряется с помощью H нормы ∞ (пикового усиления) интересующей передаточной функции, такой как от нарушения порядка до сигналов ошибки. (См. H-Infinity Performance.)
Для системы T (<reservedrangesplaceholder6>), прочная эффективность <reservedrangesplaceholder5> μ является самым маленьким значением γ таким образом, что пиковая выгода T остается ниже γ по причине неопределенности до 1 / γ в нормализованных модулях. Для примера:
μ = 0,5 означает, что ||<reservedrangesplaceholder2> (s) ||∞ остается ниже 0,5 для неопределенности до удвоения неопределенности, указанной в T. Наихудший коэффициент усиления для заданной неопределенности обычно меньше.
μ = 2 означает, что ||<reservedrangesplaceholder2> (s) ||∞ остается ниже 2 для неопределенности до половины неопределенности, указанной в T. Для этого значения усиление в худшем случае для полной заданной неопределенности может быть намного больше. Он может быть даже бесконечным, что означает, что система не остается стабильной во всей области значений заданной неопределенности.
Количественная μ является пиковым значением по частоте structured singular value μ (ω) для неопределенности, указанной в T. Эта величина является обобщением сингулярного значения для неопределенных систем. Это зависит от структуры неопределенности в системе. На практике μ трудно вычислить точно, поэтому программное обеспечение вместо этого вычисляет нижнюю и верхнюю границы, и . Верхняя граница имеет несколько применений в разработке и анализе системы управления. Вы можете:
Использовать musyn чтобы спроектировать контроллер для неопределенного объекта, который минимизирует системы с обратной связью. В дополнение к полученному контроллеру, musyn возвращает соответствующее значение в CLperf выходной аргумент.
Использовать musynperf оценить устойчивую эффективность неопределенной системы. Эта функция возвращает более низкие и верхние границы μ, значения неопределенности, которые дают пиковое μ, и другую информацию об устойчивой эффективности с обратной связью.
Чтобы понять расчет прочной эффективности <reservedrangesplaceholder5> , считайте неопределенную систему T (<reservedrangesplaceholder3>), смоделированной как фиксированный фрагмент <reservedrangesplaceholder2> 0 и неопределенный фрагмент Δ <reservedrangesplaceholder1> / γ.
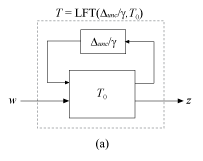
.R. unc собирает неопределенные элементы {Δ1,..., .R. N}
Каждое j И является произвольной действительной, комплексной или динамической неопределенностью, которая нормирована таким образом, что ||Δ<reservedrangesplaceholder1>||∞ ≤ 1. Коэффициент γ корректирует уровень неопределенности.
Предположим, что для системы, смоделированной как на схеме (а),
||<reservedrangesplaceholder2>||∞ ≤ γ для всех ||Δ<reservedrangesplaceholder0>||∞ ≤ 1.
Теоремой маленькой выгоды (см. [1]), это прочное условие эффективности эквивалентно заявлению, что система диаграммы (b), LFT (Δ <reservedrangesplaceholder3> / γ, T), стабильно для всех для всего ||Δ <reservedrangesplaceholder0> || ∞ ≤ 1.
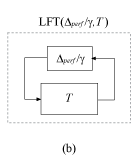
.R. perf называется performance block. Расширьтесь T как в диаграмме (a) и группе Δ <reservedrangesplaceholder1> с неопределенным Δ <reservedrangesplaceholder0> блоков, чтобы определить новый блок Δ,
Результатом является система на следующей схеме.
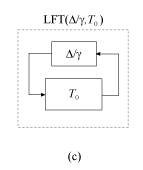
Таким образом, устойчивое условие эффективности системы схемы (a) эквивалентно условию устойчивости на схеме (c), или
Устойчивый μ эффективности является наименьшим γ, для которого это условие устойчивости. Эквивалентно, 1/ μ является самым большим уровнем неопределенности 1/ γ, для которого система диаграммы (с) устойчива. Другими словами, 1/ μ является устойчивым запасом устойчивости цикла обратной связи схемы (c) для дополненной неопределенности (Для получения дополнительной информации об устойчивых запасах устойчивости смотрите Анализ робастности и наихудшего случая.)
Чтобы получить оценку верхней границы μ, программное обеспечение вводит scalings. Если система в схеме (c) стабильна для всех ||Δ||∞ ≤ 1, то система следующей схемы также стабильна, для любого инвертируемого D.
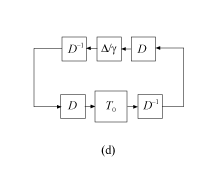
Если D коммутируется, то система схемы (d) такая же, как и система в следующей схеме.
Матрицы D, что структурно коммутируйте с, называются D масштабированиями. Они могут быть частотно-зависимыми, что обозначается D (ω).
Определить как:
Для оптимального D * (ω) и любого γ ≥,
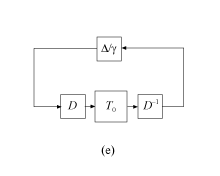
Поэтому по теореме о малом усилении система схемы (e) стабильна для всех ||Δ||∞ ≤ 1. Из этого следует, что 1 / <reservedrangesplaceholder5> ≤ 1 / μ, или <reservedrangesplaceholder3> ≤ <reservedrangesplaceholder2> , потому что 1 / μ - прочный запас устойчивости. Следовательно, μ ≤, так что является верхней границей для надежного μ эффективности. Эта верхняя граница - количество, вычисленное musynperf и оптимизировано musyn.
Когда все неопределенные элементы É j являются комплексными или динамикой LTI, программное обеспечение аппроксимирует путем выбора частотной сетки {ω 1,..., ωN}. В каждой частотной точке программное обеспечение решает оптимальную задачу масштабирования
Затем он устанавливает к наибольшему результату по всем частотам в сетке,
Когда некоторые Β j являются реальными, возможно получить менее консервативную верхнюю границу с помощью дополнительных масштабирований, называемых G масштабами. В этом случае, является наименьшим по частоте такой, что
для некоторых Dr (ωi), Dc (ωi) и Gcr (ωi). Эти частотно-зависимые матрицы являются D и G масштабированиями.
musyn команда синтезирует устойчивые контроллеры с помощью итерационного процесса, который оптимизирует устойчивую эффективность . Чтобы узнать, как использовать musyn, см. Робастное Проектирование контроллера Использование Mu-Synthesis. Для получения дополнительной информации о musyn алгоритм, см. Процесс итерации D-K.
[1] Skogestad, S. and I. Postlethwaite, Multivariable Feedback Control: Analysis and Design, 2d ed. West Sussex, England: John Wiley & Sons, 2005, pp. 156, 306.