Exponenta Banner

idnlarx

Нелинейная модель ARX

расширьте все на странице

Описание

idnlarx модель представляет нелинейную модель ARX, которая является расширением линейной структуры ARX и содержит линейные и нелинейные функции.

Нелинейная модель ARX состоит из регрессоров модели и выходной функции. Выходная функция включает линейные и нелинейные функции, которые действуют на регрессоры модели, чтобы дать выход модели и фиксированное смещение для того выхода. Эта блок-схема представляет структуру нелинейной модели ARX в сценарии симуляции.

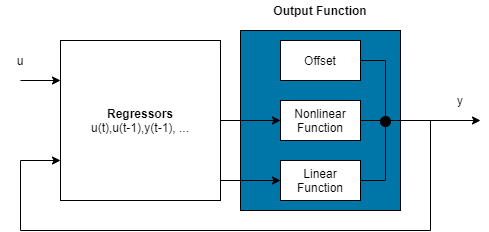
Regressor block is on the left. Output function is on the right. Output function block contains, from top to bottom, Offset, Nonlinear Function, and Linear Function. The inputs to the Regressor block are system input u and the output of the output function y.

Программное обеспечение вычисляет нелинейную модель ARX выход y на двух этапах:

  1. Это вычисляет значения регрессора из текущих и прошлых входных значений и прошлых выходных данных.

    В самом простом случае регрессоры являются задержанными вводами и выводами, такими как u (t –1) и y (t –3). Подобные регрессоры называются linear regressors. Вы задаете линейные регрессоры с помощью linearRegressor объект. Можно также задать линейные регрессоры при помощи линейных порядков модели ARX как входной параметр. Для получения дополнительной информации смотрите Нелинейные Порядки Модели ARX и Задержку. Однако этот второй подход ограничивает ваш набор регрессора к линейным регрессорам с последовательными задержками. Чтобы создать polynomial regressors, используйте polynomialRegressor объект. Можно также задать custom regressors, которые являются нелинейными функциями задержанных вводов и выводов. Например, u (t –1) y (t –3) является пользовательским регрессором, который умножает экземпляры ввода и вывода вместе. Задайте пользовательские регрессоры с помощью customRegressor объект.

    Можно присвоить любой из регрессоров как входные параметры с блоком линейной функции выходной функции, нелинейного функционального блока или обоих.

  2. Это сопоставляет регрессоры с выходом модели с помощью блока выходной функции. Блок выходной функции может включать линейные и нелинейные блоки параллельно. Например, рассмотрите следующее уравнение:

    F(x)=LT(x−r)+g(Q(x−r))+d

    Здесь, x является вектором из регрессоров, и r является средним значением x. F(x)=LT(x−r)+y0 выход блока линейной функции. g(Q(x−r))+y0 представляет выход нелинейного функционального блока. Q является матрицей проекции, которая делает вычисления хорошо подготовленными. d является скалярным смещением, которое добавляется к объединенным выходным параметрам линейных и нелинейных блоков. Точная форма F (x) зависит от вашего выбора выходной функции. Можно выбрать из доступных объектов отображения, таких как сети древовидного раздела, сети вейвлета и многоуровневые нейронные сети. Можно также исключить или линейное или нелинейный функциональный блок от выходной функции.

    При оценке нелинейной модели ARX программное обеспечение вычисляет значения параметра модели, такие как L, r, d, Q и другие параметры, задающие g.

Получившиеся нелинейные модели ARX idnlarx объекты, которые хранят все данные модели, включая регрессоры модели и параметры выходной функции. Для получения дополнительной информации об этих объектах, смотрите Нелинейные Структуры модели.

Для получения дополнительной информации о idnlarx структура модели, смотрите то, Что Нелинейные Модели ARX?.

Для idnlarx свойства объектов, смотрите Свойства.

Создание

Можно получить idnlarx объект одним из двух способов.

  • Используйте nlarx команда к оба создает idnlarx возразите и оцените параметры модели.

    sys = nlarx(data,reg)

  • Используйте idnlarx конструктор, чтобы создать нелинейную модель ARX и затем оценить использование параметров модели nlarx или pem.

    sys = idnlarx(output_name,input_name,reg)

Синтаксис

sys = idnlarx(output_name,input_name,orders)
sys = idnlarx(output_name,input_name,Regressors)
sys = idnlarx(___,OutputFcn)
sys = idnlarx(linmodel)
sys = idnlarx(linmodel,OutputFcn)
sys = idnlarx(___,Name,Value)

Описание

Задайте модель непосредственно

пример

sys = idnlarx(output_name,input_name,orders) задает набор линейных регрессоров с помощью порядков модели ARX. Используйте этот синтаксис, когда вы расширяете ARX линейная модель, или когда вы планируете использовать только регрессоры, которые линейны с последовательными задержками.

пример

sys = idnlarx(output_name,input_name,Regressors) создает нелинейную модель ARX с выходом и входными именами output_name и input_name, соответственно, и регрессор установлен в Regressors это содержит любую комбинацию линейных, полиномиальных, и пользовательских регрессоров. Программное обеспечение создает sys использование сети вейвлета по умолчанию ('idWaveletNetwork') отображение объекта для выходной функции.

пример

sys = idnlarx(___,OutputFcn) задает выходную функцию OutputFcn это сопоставляет регрессоры с выходом модели. Можно использовать этот синтаксис с любой из предыдущих комбинаций входных аргументов.

Инициализируйте значения модели Используя линейную модель

пример

sys = idnlarx(linmodel) использует линейную модель linmodel извлечь определенные свойства, такие как имена, модули и шаг расчета, и инициализировать значения линейных коэффициентов модели. Используйте этот синтаксис, когда это необходимо, чтобы создать нелинейную модель ARX как расширение, или улучшение на, существующую линейную модель.

пример

sys = idnlarx(linmodel,OutputFcn) задает выходную функцию OutputFcn это сопоставляет регрессоры с выходом модели.

Задайте свойства модели

sys = idnlarx(___,Name,Value) задает дополнительные свойства idnlarx структура модели с помощью одних или нескольких аргументов name-value.

Входные параметры

развернуть все

Модель ARX заказывает в виде матричного [na nb nk]N/A обозначает количество задержанных выходных параметров, nb обозначает количество задержанных входных параметров и nk обозначает минимальную входную задержку. Минимальная выходная задержка фиксируется к 1. Для получения дополнительной информации о том, как создать orders матрица, смотрите arx.

Когда вы задаете orders, программное обеспечение преобразует информацию для заказа в линейную форму регрессора в idnlarx Regressors свойство. Для примера смотрите, Создают Нелинейную Модель ARX Используя Порядки Модели ARX.

Дискретное время идентифицировало ввод/вывод линейная модель в виде любой линейной модели, созданной с помощью средств оценки, то есть, idpoly объект, idss объект, idtf объект или idproc объект с Ts > 0. Создайте эту модель с помощью функции конструктора для объекта или оцените модель с помощью связанной команды оценки. Например, чтобы создать модель ARX, использовать arx, и задайте получившийся idpoly возразите как linmodel.

Свойства

развернуть все

Спецификация регрессора в виде вектор-столбца, содержащего один или несколько объектов спецификации регрессора, которые являются linearRegressor объекты, polynomialRegressor объекты и customRegressor customRegressor объекты. Каждый объект задает формулу для генерации регрессоров от изолированных переменных. Например:

  • L = linearRegressor({'y1','u1'},{1,[2 5]}) генерирует регрессоры y1 (t –1), u1 (t –2), и u2 (t –5).

  • P = polynomialRegressor('y2',4:7,2) генерирует регрессоры y2 (t –4)2, y2 (t –5)2, y2 (t –6)2, и y2 (t –7)2.

  • C = customRegressor({'y1','u1','u2'},{1 2 2},@(x,y,z)sin(x.*y+z)) генерирует один sin регрессора (y1 (t –1) u1 (t –2) +u2 (t –2)

    .

Для примера, который реализует эти регрессоры, смотрите, Создают и Типы Регрессора Объединения.

Чтобы добавить регрессоры в существующую модель, создайте вектор из объектов спецификации и используйте запись через точку, чтобы установить Regressors к этому вектору. Например, следующий код сначала создает idnlarx модель sys и затем добавляет, что регрессор возражает LP, и C к регрессорам sys.

sys = idnlarx({'y1','y2'},{'u1','u2'});
R = [L;P;C];
sys.Regressors = R;

Для примера создания и использования линейного набора регрессора, смотрите, Создают Нелинейную Модель ARX Используя Линейные Регрессоры.

Выходная функция, которая сопоставляет регрессоры idnlarx модель в выход модели в виде массива столбца, содержащего нуль или больше следующих строк или сопоставляющего объекты:

'idWaveletNetwork' или idWaveletNetwork объектСеть Wavelet
'idLinear' или '' или [] или idLinear объектЛинейная функция
'idSigmoidNetwork' или idSigmoidNetwork объектСигмоидальная сеть
'idTreePartition' или idTreePartition объектМодель регрессии раздела двоичного дерева
'idGaussianProcess' или idGaussianProcess объектГауссова модель регрессии процесса (требует Statistics and Machine Learning Toolbox™),
'idTreeEnsemble' или idTreeEnsembleМодель ансамбля дерева регрессии (Statistics and Machine Learning Toolbox)
idFeedforwardNetwork объектНейронная сеть — Многоуровневая сеть прямого распространения Deep Learning Toolbox™.
idCustomNetwork объектПользовательская сеть — Подобно idSigmoidNetwork, но с пользовательской заменой для сигмоидальной функции.

idWaveletNetwork, idSigmoidNetwork, idTreePartition, и idCustomNetwork объекты содержат и линейные и нелинейные компоненты. Можно удалить (не, используют), линейные компоненты idWaveletNetwork, idSigmoidNetwork, и idCustomNetwork путем установки LinearFcn.Use значение к false.

idFeedforwardNetwork функция имеет только нелинейный компонент, который является network Объект (Deep Learning Toolbox) Deep Learning Toolbox. idLinear функция, когда имя подразумевает, имеет только линейный компонент.

Определение вектора символов, например 'idSigmoidNetwork', создает объект отображения с настройками по умолчанию. В качестве альтернативы можно задать свойства объектов отображения двумя другими способами:

  • Создайте объект отображения использование аргументов, чтобы изменить свойства по умолчанию.

    MO = idSigmoidNetwork(15)

  • Создайте отображение значения по умолчанию, возражают сначала и затем используют запись через точку, чтобы изменить свойства.

    MO = idSigmoidNetwork;
MO.NumberOfUnits = 15

Для ny каналы выхода можно задать объекты отображения индивидуально для каждого канала установкой OutputFcn к массиву объектов отображения ny. Например, следующий код задает OutputFcn использование записи через точку для системы с двумя входными каналами и двумя выходными каналами. 

sys = idnlarx({'y1','y2'},{'u1','u2'});
sys.OutputFcn = [idWaveletNetwork; idSigmoidNetwork]
Чтобы задать то же отображение для всех выходных параметров, задайте OutputFcn как вектор символов или один объект отображения.

OutputFcn представляет статическую функцию отображения, которая преобразовывает регрессоры нелинейной модели ARX в выход модели. OutputFcn является статическим, потому что это не зависит от времени. Например, если y(t)=y0+a1y(t−1)+a2y(t−2)+…+b1u(t−1)+b2u(t−2)+…, затем OutputFcn линейная функция, представленная idLinear объект.

Для примера определения выходной функции смотрите, Задают Выходную функцию для Нелинейной Модели ARX.

Присвоения регрессора на линейные и нелинейные компоненты нелинейной модели ARX в виде nr-by-nc таблица с логическими записями, которые задают который регрессоры использовать для который компонент. Здесь, nr является количеством регрессоров. nc является общим количеством линейных и нелинейных компонентов в OutputFcn. Строки таблицы соответствуют отдельным регрессорам. Имена строки определяются к именам регрессора. Если табличным значением для строки, i и компонент индексируют j, является true, затем i th регрессор является входом к линейному или нелинейному j компонента.

Для мультивыходных систем, OutputFcn содержит один объект отображения для каждого выхода. Каждый объект отображения может использовать и линейные и нелинейные компоненты или только один из этих двух компонентов.

Для примера просмотра и изменения RegressorUsage свойство, смотрите, Изменяют Присвоения Регрессора на Компоненты Выходной функции.

Это свойство доступно только для чтения.

Сводный отчет, который содержит информацию об опциях оценки и результатах для нелинейной модели ARX, полученной с помощью nlarx команда. Используйте Report найти информацию об оценке для идентифицированной модели, включая:

  • Метод оценки

  • Опции оценки

  • Поисковые условия завершения

  • Совпадение данных оценки

Содержимое Report не важны, если модель была создана с помощью idnlarx.

sys = idnlarx('y1','u1',reg);
sys.Report.OptionsUsed
ans =

     []

Если вы используете nlarx оценить модель, поля Report содержите информацию о данных об оценке, опциях и результатах.

load iddata1;
sys = nlarx(z1,reg);
m.Report.OptionsUsed
Option set for the nlarx command:

  IterativeWavenet: 'auto'
             Focus: 'prediction'
           Display: 'off'
    Regularization: [1x1 struct]
      SearchMethod: 'auto'
     SearchOptions: [1x1 idoptions.search.identsolver]
      OutputWeight: 'noise'
          Advanced: [1x1 struct]

Для получения дополнительной информации об этом свойстве и как использовать его, см. Выходные аргументы в nlarx страница с описанием и Отчет Оценки.

Независимая переменная для входных параметров, выходных параметров, и — когда доступный — внутренние состояния в виде вектора символов.

Шумовое отклонение (ковариационная матрица) инноваций модели e. Алгоритм оценки обычно устанавливает это свойство. Однако можно также присвоить значения ковариации путем определения ny- ny матрица.

Шаг расчета в виде положительной скалярной величины, представляющей период выборки. Это значение описывается в модуле, заданном TimeUnit свойство модели.

Модули для переменной времени, шаг расчета Ts, и любые задержки модели в виде одного из следующих значений:

  • 'nanoseconds'

  • 'microseconds'

  • 'milliseconds'

  • 'seconds'

  • 'minutes'

  • 'hours'

  • 'days'

  • 'weeks'

  • 'months'

  • 'years'

Изменение этого свойства не оказывает влияния на другие свойства, и поэтому изменяет полное поведение системы. Использование chgTimeUnit (Control System Toolbox), чтобы преобразовать между единицами измерения времени, не изменяя поведение системы.

Введите названия канала в виде одного из следующего:

  • Вектор символов — Для моделей одно входа, например, 'controls'.

  • Массив ячеек из символьных векторов Модели мультивхода For.

Входными именами в моделях Nonlinear ARX должен быть допустимый MATLAB® имена переменных после того, как вы удаляете любые пробелы.

В качестве альтернативы используйте автоматическое векторное расширение, чтобы присвоить входные имена для мультивходных моделей. Например, если sys 2D входная модель, введите:

sys.InputName = 'controls';

Входные имена автоматически расширяются до {'controls(1)';'controls(2)'}.

Когда вы оцениваете модель с помощью iddata объект, data, программное обеспечение автоматически устанавливает InputName к data.InputName.

Можно использовать краткое обозначение u относиться к InputName свойство. Например, sys.u эквивалентно sys.InputName.

Входные названия канала имеют несколько использования, включая:

  • Идентификация каналов на отображении модели и графиках

  • Извлечение подсистем систем MIMO

  • Определение точек контакта, когда взаимосвязанные модели

Введите модули канала в виде одного из следующего:

  • Вектор символов — Для моделей одно входа, например, 'seconds'.

  • Массив ячеек из символьных векторов Модели мультивхода For.

Используйте InputUnit отслеживать модули входного сигнала. InputUnit не оказывает влияния на поведение системы.

Введите группы канала. InputGroup свойство позволяет вам присвоить входные каналы систем MIMO в группы и обратиться к каждой группе по наименованию. Задайте входные группы как структуру. В этой структуре имена полей являются названиями группы, и значения полей являются входными каналами, принадлежащими каждой группе. Например:

sys.InputGroup.controls = [1 2];
sys.InputGroup.noise = [3 5];

создает входные группы под названием controls и noise это включает входные каналы 1, 2 и 3, 5, соответственно. Можно затем извлечь подсистему из controls входные параметры ко всему выходному использованию:

sys(:,'controls')

Выведите названия канала в виде одного из следующего:

  • Вектор символов — Для моделей одно выхода. Например, 'measurements'.

  • Массив ячеек из символьных векторов For модели мультивыхода.

Выходные имена в моделях Nonlinear ARX должны быть допустимыми именами переменной MATLAB после того, как вы удалите любые пробелы.

В качестве альтернативы используйте автоматическое векторное расширение, чтобы присвоить выходные имена для мультивыходных моделей. Например, если sys 2D выходная модель, введите:

sys.OutputName = 'measurements';

Выходные имена автоматически расширяются до {'measurements(1)';'measurements(2)'}.

Когда вы оцениваете модель с помощью iddata объект, data, программное обеспечение автоматически устанавливает OutputName к data.OutputName.

Можно использовать краткое обозначение y относиться к OutputName свойство. Например, sys.y эквивалентно sys.OutputName.

Выходные названия канала имеют несколько использования, включая:

  • Идентификация каналов на отображении модели и графиках

  • Извлечение подсистем систем MIMO

  • Определение точек контакта, когда взаимосвязанные модели

Выведите модули канала в виде одного из следующего:

  • Вектор символов — Для моделей одно выхода. Например, 'seconds'.

  • Массив ячеек из символьных векторов For модели мультивыхода.

Используйте OutputUnit отслеживать модули выходного сигнала. OutputUnit не оказывает влияния на поведение системы.

Выведите группы канала. OutputGroup свойство позволяет вам присвоить выходные каналы систем MIMO в группы и обратиться к каждой группе по наименованию. Задайте выходные группы как структуру. В этой структуре имена полей являются названиями группы, и значения полей являются выходными каналами, принадлежащими каждой группе. Например:

sys.OutputGroup.temperature = [1];
sys.InputGroup.measurement = [3 5];

создает выходные группы под названием temperature и measurement это включает выходные каналы 1, и 3, 5, соответственно. Можно затем извлечь подсистему от всех входных параметров до measurement выходное использование:

sys('measurement',:)

Имя системы в виде вектора символов. Например, 'system 1'.

Любой текст, который вы хотите сопоставить с системой в виде строки или массива ячеек из символьных векторов. Свойство хранит, какой бы ни тип данных вы обеспечиваете. Например, если sys1 и sys2 модели динамической системы, можно установить их Notes свойства можно следующим образом.

sys1.Notes = "sys1 has a string.";
sys2.Notes = 'sys2 has a character vector.';
sys1.Notes
sys2.Notes
ans = 

    "sys1 has a string."


ans =

    'sys2 has a character vector.'

Любые данные вы хотите сопоставить с системой в виде любого типа данных MATLAB.

Функции объекта

Для получения информации об объектных функциях для idnlarx, см. Нелинейные Модели ARX.

Примеры

свернуть все

Скрипт Open Live Script

Создайте idnlarx модель путем определения модели ARX заказывает вектор.

Создайте вектор порядка из формы [na nb nk], где na и nb порядки полиномов модели A и B ARX и nk количество задержек ввода/вывода.

na = 2;
nb = 3;
nk = 5;
orders = [na nb nk];

Создайте нелинейную модель ARX sys.

output_name = 'y1';
input_name = 'u1';

sys = idnlarx(output_name,input_name,[2 3 5]);

Просмотрите выходную функцию.

disp(sys.OutputFcn)
Wavelet Network

 Nonlinear Function: Wavelet network with number of units chosen automatically
 Linear Function: uninitialized
 Output Offset: uninitialized

                Input: '<Function inputs>'
               Output: '<Function output>'
            LinearFcn: '<Linear function parameters>'
         NonlinearFcn: '<Wavelet and scaling function units and their parameters>'
               Offset: '<Offset parameters>'
    EstimationOptions: '<Estimation options>'

По умолчанию модель использует сеть вейвлета, представленную idWaveletNetwork объект, для выходной функции. idWaveletNetwork объект включает линейные и нелинейные компоненты.

Просмотрите Regressors свойство.

disp(sys.Regressors)
Linear regressors in variables y1, u1
       Variables: {'y1'  'u1'}
            Lags: {[1 2]  [5 6 7]}
     UseAbsolute: [0 0]
    TimeVariable: 't'

idnlarx конструктор преобразовывает порядки модели в Regressors форма.

  • Lags массив для y1, [1 2], эквивалентно na значение 2. Обе формы задают два последовательных выходных регрессора, y1(t-1) и y1(t-2).

  • Lags массив для u1, [5 6 7], включает три задержки, заданные nb значение 3, и переключает их nk значение 5. Входными регрессорами является поэтому u1(t-5), u1(t-6), и u1(t-7).

Просмотрите регрессоры.

getreg(sys)
ans = 5x1 cell
    {'y1(t-1)'}
    {'y1(t-2)'}
    {'u1(t-5)'}
    {'u1(t-6)'}
    {'u1(t-7)'}

Можно использовать orders синтаксис, чтобы задать простые линейные регрессоры. Однако, чтобы создать более комплексные регрессоры, используйте команды регрессора linearRegressor, polynomialRegressor, и customRegressor создать объединенный регрессор для Regressors синтаксис.

Скрипт Open Live Script

Создайте idnlarx модель путем определения линейных регрессоров.

Создайте линейный регрессор, который содержит две выходных задержки и две входных задержки.

output_name = 'y1';
input_name = 'u1';
var_names = {output_name,input_name};

output_lag = [1 2];
input_lag = [1 2];
lags = {output_lag,input_lag};

reg = linearRegressor(var_names,lags)
reg = 
Linear regressors in variables y1, u1
       Variables: {'y1'  'u1'}
            Lags: {[1 2]  [1 2]}
     UseAbsolute: [0 0]
    TimeVariable: 't'

  Regressors described by this set

Модель содержит регрессоры y(t-1), y(t-2), u(t-1), и u(t-2).

Создайте idnlarx модель и представление регрессоры.

sys = idnlarx(output_name,input_name,reg);
getreg(sys)
ans = 4x1 cell
    {'y1(t-1)'}
    {'y1(t-2)'}
    {'u1(t-1)'}
    {'u1(t-2)'}

Просмотрите выходную функцию.

disp(sys.OutputFcn)
Wavelet Network

 Nonlinear Function: Wavelet network with number of units chosen automatically
 Linear Function: uninitialized
 Output Offset: uninitialized

                Input: '<Function inputs>'
               Output: '<Function output>'
            LinearFcn: '<Linear function parameters>'
         NonlinearFcn: '<Wavelet and scaling function units and their parameters>'
               Offset: '<Offset parameters>'
    EstimationOptions: '<Estimation options>'

Просмотрите таблицу использования регрессора.

disp(sys.RegressorUsage)
               y1:LinearFcn    y1:NonlinearFcn
               ____________    _______________

    y1(t-1)       true              true      
    y1(t-2)       true              true      
    u1(t-1)       true              true      
    u1(t-2)       true              true

Все регрессоры являются входными параметрами и к линейным и к нелинейным компонентам wavenet объект.

Скрипт Open Live Script

Создайте нелинейную модель ARX с линейным набором регрессора.

Создайте линейный регрессор, который содержит три выходных задержки и две входных задержки.

output_name = 'y1';
input_name = 'u1';
var_names = {output_name,input_name};

output_lag = [1 2 3];
input_lag = [1 2];
lags = {output_lag,input_lag};

reg = linearRegressor(var_names,lags)
reg = 
Linear regressors in variables y1, u1
       Variables: {'y1'  'u1'}
            Lags: {[1 2 3]  [1 2]}
     UseAbsolute: [0 0]
    TimeVariable: 't'

  Regressors described by this set

Создайте нелинейную модель ARX.

sys = idnlarx(output_name,input_name,reg);

Просмотрите Regressors свойство.

disp(sys.Regressors)
Linear regressors in variables y1, u1
       Variables: {'y1'  'u1'}
            Lags: {[1 2 3]  [1 2]}
     UseAbsolute: [0 0]
    TimeVariable: 't'

sys использование idWavenetNetwork как выходная функция по умолчанию. Реконфигурируйте выходную функцию к idSigmoidNetwork.

sys.OutputFcn = 'idSigmoidNetwork';
disp(sys.OutputFcn)
Sigmoid Network

 Nonlinear Function: Sigmoid network with 10 units
 Linear Function: uninitialized
 Output Offset: uninitialized

           Input: '<Function inputs>'
          Output: '<Function output>'
       LinearFcn: '<Linear function parameters>'
    NonlinearFcn: '<Sigmoid units and their parameters>'
          Offset: '<Offset parameters>'
Скрипт Open Live Script

Задайте сигмоидальную сетевую выходную функцию, когда вы создадите нелинейную модель ARX.

Присвойте имена переменных и задайте набор регрессора.

output_name = 'y1';
input_name = 'u1';
r = linearRegressor({output_name,input_name},{1 1});

Создайте нелинейную модель ARX, которая задает idSigmoidNetwork выходная функция. Определите номер терминов в сигмоидальном расширении на 15.

sys = idnlarx(output_name,input_name,r,idSigmoidNetwork(15));

Просмотрите спецификацию выходной функции.

disp(sys.OutputFcn)
Sigmoid Network

 Nonlinear Function: Sigmoid network with 15 units
 Linear Function: uninitialized
 Output Offset: uninitialized

           Input: '<Function inputs>'
          Output: '<Function output>'
       LinearFcn: '<Linear function parameters>'
    NonlinearFcn: '<Sigmoid units and their parameters>'
          Offset: '<Offset parameters>'
Скрипт Open Live Script

Создайте idnlarx модель, которая использует только линейное отображение в выходной функции. Значение аргумента [] эквивалентно значению аргумента idLinear.

sys = idnlarx([2 2 1],[])
sys = 
Nonlinear ARX model with 1 output and 1 input
  Inputs: u1
  Outputs: y1

Regressors:
  Linear regressors in variables y1, u1
  List of all regressors

Output function: None
Sample time: 1 seconds

Status:                                                         
Created by direct construction or transformation. Not estimated.
Скрипт Open Live Script

Создайте набор регрессора, который включает линейные, полиномиальные, и пользовательские регрессоры.

Задайте L как набор линейных регрессоров y1(t-1), u1(t-2), и u1(t-5).

L = linearRegressor({'y1','u1'},{1, [2 5]});

Задайте P как набор полиномиальных регрессоров y2(t-4)2, y2(t-5)2, y2(t-6)2, и y2(t-7)2.

P = polynomialRegressor('y2',4:7,2);

Задайте C как пользовательский регрессор sin(y1(t-1)u1(t-2)+u2(t-2)), использование @ символ, чтобы создать указатель анонимной функции.

C = customRegressor({'y1','u1','u2'},{1 2 2},@(x,y,z)sin(x.*y+z));

Объединитесь регрессоры в один регрессор устанавливают R.

R = [L;P;C]
R = 
[3 1] array of linearRegressor, polynomialRegressor, customRegressor objects.
------------------------------------
1. Linear regressors in variables y1, u1
       Variables: {'y1'  'u1'}
            Lags: {[1]  [2 5]}
     UseAbsolute: [0 0]
    TimeVariable: 't'

------------------------------------
2. Order 2 regressors in variables y2
               Order: 2
           Variables: {'y2'}
                Lags: {[4 5 6 7]}
         UseAbsolute: 0
    AllowVariableMix: 0
         AllowLagMix: 0
        TimeVariable: 't'

------------------------------------
3. Custom regressor: sin(y1(t-1).*u1(t-2)+u2(t-2))
    VariablesToRegressorFcn: @(x,y,z)sin(x.*y+z)
                  Variables: {'y1'  'u1'  'u2'}
                       Lags: {[1]  [2]  [2]}
                 Vectorized: 1
               TimeVariable: 't'

 
Regressors described by this set

Создайте нелинейную модель ARX.

sys = idnlarx({'y1','y2'},{'u1','u2'},R)
sys = 
Nonlinear ARX model with 2 outputs and 2 inputs
  Inputs: u1, u2
  Outputs: y1, y2

Regressors:
  1. Linear regressors in variables y1, u1
  2. Order 2 regressors in variables y2
  3. Custom regressor: sin(y1(t-1).*u1(t-2)+u2(t-2))
  List of all regressors

Output functions:
  Output 1:  Wavelet network with number of units chosen automatically
  Output 2:  Wavelet network with number of units chosen automatically

Sample time: 1 seconds

Status:                                                         
Created by direct construction or transformation. Not estimated.
Скрипт Open Live Script

Используйте линейную модель ARX вместо набора регрессора, чтобы создать нелинейную модель ARX.

Создайте линейную модель ARX с помощью idpoly.

A = [1 -1.2 0.5];
B = [0.8 1];
LinearModel = idpoly(A, B, 'Ts', 0.1);

Задайте имена ввода и вывода для модели с помощью записи через точку.

LinearModel.OutputName = 'y1';
LinearModel.InputName = 'u1';

Создайте нелинейную модель ARX с помощью линейной модели ARX.

m1 = idnlarx(LinearModel)
m1 = 
Nonlinear ARX model with 1 output and 1 input
  Inputs: u1
  Outputs: y1

Regressors:
  Linear regressors in variables y1, u1
  List of all regressors

Output function: Wavelet network with number of units chosen automatically
Sample time: 0.1 seconds

Status:                                                         
Created by direct construction or transformation. Not estimated.

Можно создать линейную модель ARX с любого идентифицированного дискретного времени линейная модель.

Оцените модель в пространстве состояний второго порядка из данных об оценке z1.

load iddata1 z1
ssModel = ssest(z1,2,'Ts',0.1);

Создайте нелинейную модель ARX из ssModel. Программное обеспечение использует имена ввода и вывода что ssModel извлечения из z1.

m2 = idnlarx(ssModel)
m2 = 
Nonlinear ARX model with 1 output and 1 input
  Inputs: u1
  Outputs: y1

Regressors:
  Linear regressors in variables y1, u1
  List of all regressors

Output function: Wavelet network with number of units chosen automatically
Sample time: 0.1 seconds

Status:                                                         
Created by direct construction or transformation. Not estimated.
Скрипт Open Live Script

Измените присвоения регрессора путем изменения RegressorUsage таблица.

Создайте нелинейную модель ARX, которая имеет два входных параметров и два выходных параметров.

Создайте имена переменных и регрессоры.

varnames = {'y1','y2','u1','u2'};
lags = {[1 2 3],[1 2],[1 2],[1 3]};
reg = linearRegressor(varnames,lags);

Создайте спецификацию выходной функции fcn это использует idWaveletNetwork для отображения регрессоров к выходу y1 и idSigmoidNetwork для отображения регрессоров к выходу y2. И сопоставляющие объекты содержат линейные и нелинейные компоненты.

fcn = [idWaveletNetwork;idSigmoidNetwork];

Создайте нелинейную модель ARX.

output_name = {'y1' 'y2'};
input_name = {'u1' 'u2'};
sys = idnlarx(output_name,input_name,reg,fcn)
sys = 
Nonlinear ARX model with 2 outputs and 2 inputs
  Inputs: u1, u2
  Outputs: y1, y2

Regressors:
  Linear regressors in variables y1, y2, u1, u2
  List of all regressors

Output functions:
  Output 1:  Wavelet network with number of units chosen automatically
  Output 2:  Sigmoid network with 10 units

Sample time: 1 seconds

Status:                                                         
Created by direct construction or transformation. Not estimated.

Отобразите RegressorUsage таблица.

disp(sys.RegressorUsage)
               y1:LinearFcn    y1:NonlinearFcn    y2:LinearFcn    y2:NonlinearFcn
               ____________    _______________    ____________    _______________

    y1(t-1)       true              true             true              true      
    y1(t-2)       true              true             true              true      
    y1(t-3)       true              true             true              true      
    y2(t-1)       true              true             true              true      
    y2(t-2)       true              true             true              true      
    u1(t-1)       true              true             true              true      
    u1(t-2)       true              true             true              true      
    u2(t-1)       true              true             true              true      
    u2(t-3)       true              true             true              true

Строки таблицы представляют регрессоры. Первые два столбца таблицы представляют линейные и нелинейные компоненты отображения с выходом y1 (idWaveletNetwork). Последние два столбца представляют два компонента отображения с выходом y2 (idSigmoidNetwork).

В этой таблице все регрессоры ввода и вывода являются входными параметрами ко всем компонентам.

Удалите y2(t-2) регрессор от y2 нелинейный компонент.

sys.RegressorUsage{4,4} = false;
disp(sys.RegressorUsage)
               y1:LinearFcn    y1:NonlinearFcn    y2:LinearFcn    y2:NonlinearFcn
               ____________    _______________    ____________    _______________

    y1(t-1)       true              true             true              true      
    y1(t-2)       true              true             true              true      
    y1(t-3)       true              true             true              true      
    y2(t-1)       true              true             true              false     
    y2(t-2)       true              true             true              true      
    u1(t-1)       true              true             true              true      
    u1(t-2)       true              true             true              true      
    u2(t-1)       true              true             true              true      
    u2(t-3)       true              true             true              true

Таблица показывает false для этой пары компонента регрессором.

Сохраните имена регрессора в Names.

Names = sys.RegressorUsage.Properties.RowNames;

Определите индексы строк, которые содержат y1 или y2 и установленный соответствующие значения y1:NonlinearFcn к False.

idx = contains(Names,'y1')|contains(Names,'y2');
sys.RegressorUsage{idx,2} = false;
disp(sys.RegressorUsage)
               y1:LinearFcn    y1:NonlinearFcn    y2:LinearFcn    y2:NonlinearFcn
               ____________    _______________    ____________    _______________

    y1(t-1)       true              false            true              true      
    y1(t-2)       true              false            true              true      
    y1(t-3)       true              false            true              true      
    y2(t-1)       true              false            true              false     
    y2(t-2)       true              false            true              true      
    u1(t-1)       true              true             true              true      
    u1(t-2)       true              true             true              true      
    u2(t-1)       true              true             true              true      
    u2(t-3)       true              true             true              true

Табличные значения отражают новые присвоения.

RegressorUsage таблица обеспечивает полную гибкость для того, чтобы индивидуально управлять присвоениями регрессора.

Больше о

развернуть все

Вопросы совместимости

развернуть все

Не рекомендуемый запуск в R2021b

Не рекомендуемый запуск в R2021a

Смотрите также

| | | | | | | | | | | |

Темы

Представленный в R2007a

Документация System Identification Toolbox

Поддержка