Цифровая модуляция

В большей части медиа-контента для коммуникации только фиксированная область значений частот доступна для передачи. Один способ передать сообщение сигнализирует, чей спектр частоты не находится в пределах той области значений фиксированной частоты, или тот, который является в противном случае неподходящим для канала, должен изменить transmittable сигнал согласно информации в вашем сигнале сообщения. Это изменение называется модуляцией, и это - модулируемый сигнал, что вы передаете. Получатель затем восстанавливается, исходный сигнал посредством процесса вызвал демодуляцию.

Цифровые функции модуляции
Сигналы и задержки
Модуляция PM
Модуляция AM
Модуляция CPM
Точный алгоритм LLR
Аппроксимируйте алгоритм LLR
Задержки цифровой модуляции
Выбранная библиография для цифровой модуляции

Цифровые функции модуляции

Методы модуляции
Основная полоса и симуляция полосы пропускания
Терминология модуляции
Представление цифровых сигналов

Методы модуляции

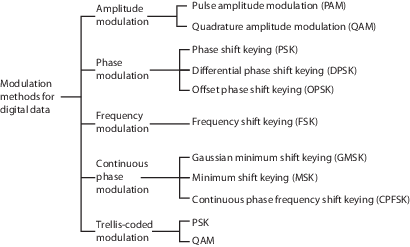
Communications Toolbox™ поддерживает эти методы модуляции для цифровых данных. Все методы в ультраправом реализованы в блоках библиотеки.

Как аналоговая модуляция, цифровая модуляция изменяет transmittable сигнал согласно информации в сигнале сообщения. Однако для цифровой модуляции сигнал сообщения ограничивается конечным множеством. Функции модуляции выводят комплексный конверт модулируемого сигнала. Используя Communications Toolbox, можно модулировать или демодулировать сигналы с помощью различных цифровых методов модуляции и построить сигнальные созвездия.

Примечание

Если в противном случае не обозначено, функции модуляции и демодуляции не выполняют импульсное формирование или фильтрацию. Смотрите Объединяющееся Импульсное Формирование и Фильтрацию с Модуляцией для получения дополнительной информации о фильтрации.

Доступные методы модуляции зависят от того, является ли входной сигнал аналогом или цифровой. Для списка методов модуляции поддержки Communications Toolbox видят Цифровую Основополосную Модуляцию, Аналоговую Основополосную Модуляцию и Аналоговую Модуляцию Полосы пропускания.

Доступ к Цифровым Блокам Модуляции. Откройте библиотеку Modulation путем двойного клика по значку в основной библиотеке блоков. Затем откройте подбиблиотеку Digital Baseband путем двойного клика по ее значку в библиотеке Modulation.

Библиотека Digital Baseband имеет собственные подбиблиотеки. Откройте каждую из этих подбиблиотек путем двойного клика по значку, перечисленному в таблице ниже.

Вид модуляции	Значок в цифровой основополосной библиотеке
Амплитудная модуляция	AM
Модуляция фазы	\pm
Модуляция частоты	FM
Непрерывная модуляция фазы	CPM
Закодированная решеткой модуляция	TCM

Некоторые цифровые подбиблиотеки модуляции содержат блоки, которые реализуют определенные методы модуляции. Эти блоки модуляции конкретного случая используют тот же вычислительный код, который их общие дубликаты используют, но обеспечивают интерфейс, который или более прост или более подходит для конкретного случая. Эта таблица приводит общие модуляторы наряду с условиями, при которых общий модулятор, эквивалентно определенному модулятору. Ситуация аналогична для демодуляторов.

Общие и частные блоки

Общий модулятор	Общие условия модулятора	Определенный модулятор
Общая основная полоса модулятора QAM	Предопределенная совокупность, содержащая 2^K, указывает на прямоугольной решетке. K является порядком модуляции.	Прямоугольная основная полоса модулятора QAM
Основная полоса модулятора M-PSK	Параметром M-ary number является `2`.	Основная полоса модулятора BPSK
Основная полоса модулятора M-PSK	Параметром M-ary number является `4`.	Основная полоса модулятора QPSK
Основная полоса модулятора M-DPSK	Параметром M-ary number является `2`.	Основная полоса модулятора DBPSK
Основная полоса модулятора M-DPSK	Параметром M-ary number является `4`.	Основная полоса модулятора DQPSK
Основная полоса модулятора CPM	Параметром M-ary number является `2`, параметром Frequency pulse shape является `Gaussian`.	Основная полоса модулятора GMSK
	Параметром M-ary number является 2, параметром Frequency pulse shape является `Rectangular`, параметром Pulse length является `1`.	Основная полоса модулятора MSK
	Параметром Frequency pulse shape является `Rectangular`, параметром Pulse length является `1`.	Основная полоса модулятора CPFSK
Общий энкодер TCM	Предопределенное сигнальное созвездие, содержащее 2^K, указывает на прямоугольной решетке.	Прямоугольный энкодер QAM TCM
Общий энкодер TCM	Предопределенное сигнальное созвездие, содержащее 2^K, указывает на круге.	Энкодер M-PSK TCM

Кроме того, блок CPFSK Modulator Baseband подобен блоку M-FSK Modulator Baseband, когда блок M-FSK использует непрерывные переходы фазы. Однако функции M-FSK этого продукта отличаются от функций CPFSK в своих интерфейсах маски и в реализациях демодулятора.

Основная полоса и симуляция полосы пропускания

Для данного метода модуляции два способа моделировать методы модуляции называются основной полосой и полосой пропускания. Основополосная симуляция, также известная как lowpass эквивалентный метод, требует меньшего количества вычисления. Communications Toolbox поддерживает основополосную симуляцию для цифровой модуляции и симуляцию полосы пропускания для аналоговой модуляции.

Основополосные модулируемые заданные сигналы

Если вы используете основополосную модуляцию, чтобы произвести комплексный конверт, y модуляции сообщения сигнализирует о x, то y является сигналом с комплексным знаком, который связан с выводом модулятора полосы пропускания. Если модулируемый сигнал имеет форму волны

$Y_{1} (t) потому что (2 π f_{c} t + θ) - Y_{2} (t) \sin (2 π f_{c} t + θ),$

где f _c является несущей частотой, и θ является начальной фазой сигнала поставщика услуг, затем основополосная симуляция распознает, что это равняется действительной части

$[(Y_{1} (t) + j Y_{2} (t)) e^{j θ}] \exp (j 2 π f_{c} t) .$

и модели только часть в квадратных скобках. Здесь j является квадратным корнем из-1. Комплексный вектор y является выборкой комплексного сигнала

$(Y_{1} (t) + j Y_{2} (t)) e^{j θ} .$

Если вы предпочитаете работать с сигналами полосы пропускания вместо основополосных сигналов, то можно создать функции, которые преобразовывают между двумя. Следует иметь в виду, что модуляция полосы пропускания имеет тенденцию быть более в вычислительном отношении интенсивной, чем основополосная модуляция, потому что сигнал поставщика услуг обычно должен выбираться на высоком показателе.

Терминология модуляции

Модуляция является процессом, которым сигнал поставщика услуг изменен согласно информации в сигнале сообщения. Несущая частота, F _c, является частотой сигнала поставщика услуг. Уровень выборки является уровнем, на котором сигнал сообщения выбирается во время симуляции.

Частота сигнала поставщика услуг обычно намного больше, чем самая высокая частота сигнала входного сигнала. Теорема отсчетов Найквиста требует, чтобы уровень выборки симуляции, F _s, был больше, чем два раза сумма несущей частоты и самая высокая частота модулируемого сигнала для демодулятора, чтобы восстановить сообщение правильно.

Представление цифровых сигналов

Чтобы модулировать сигнал с помощью цифровой модуляции с алфавитом, имеющим M символы, запустите с действительного сигнала сообщения, значения которого являются целыми числами от 0 до M-1. Представляйте сигнал путем листинга его значений в векторе, x. Также можно использовать матрицу, чтобы представлять многоканальный сигнал, где каждый столбец матрицы представляет один канал.

Например, если модуляция использует алфавит с восемью символами, то векторный [2 3 7 1 0 5 5 2 6]' является допустимым одноканальным входом к модулятору. Как многоканальный пример, матрица 2D столбца

[2 3;
 3 3;
 7 3;
 0 3;]

задает двухканальный сигнал, в котором второй канал имеет постоянное значение 3.

Сигналы и задержки

Вся цифровая модуляция блокирует процесс только сигналы дискретного времени и использование основополосное представление. Типы данных вводов и выводов изображены в следующей фигуре.

Примечание

Если вы хотите разделить синфазные компоненты и квадратурные компоненты комплекса модулируемый сигнал, используйте блок Complex to Real-Imag в библиотеке Simulink Math Operations.

Сигналы с целочисленным знаком и сигналы с бинарным знаком

Некоторые цифровые блоки модуляции могут принять или сигналы с бинарным знаком или с целочисленным знаком. Соответствующие блоки демодуляции могут вывести или целые числа или группы отдельных битов, которые представляют целые числа. В этом разделе описывается модуляция блокирует целое число процесса или двоичные входы; случай для блоков демодуляции является реверсом. Необходимо отметить, что блоки модуляции имеют параметр Input type и что блоки демодуляции имеют параметр Output type.

Когда вы устанавливаете параметр Input type на Integer, блок принимает целочисленные значения от 0 до M-1. M представляет параметры блоков M-ary number.

Когда вы устанавливаете параметр Input type на Bit, блок принимает входные параметры с бинарным знаком, которые представляют целые числа. Блок собирает сигналы с бинарным знаком в группы K = _log2 (M) биты

где

K представляет количество битов на символ. Начиная с M = 2^K, K обычно упоминается как порядок модуляции.

Длина входного вектора должна быть целочисленным кратным K. В этой настройке блок принимает группу битов K и сопоставляет ту группу на символ в блоке вывод. Блок выводит модулируемый символ того для каждой группы битов K.

Упорядоченное расположение совокупности (или Symbol Set Ordering)

В зависимости от схемы модуляции, Constellation ordering или параметра Symbol set ordering указывает как блок-диаграммы группа битов входа K к соответствующему символу. Когда вы устанавливаете параметр на Binary, блок-диаграммы [u (1) u (2) ... u (K)] к целому числу

$\sum_{i = 1}^{K} u (i) 2^{K - i}$

и принимает, что это целое число является входным значением. u (1) старший значащий бит.

Если вы устанавливаете M = 8, Constellation ordering (или Symbol set ordering) к Binary, и слово двоичного входа [1 1 0], блок преобразовывает [1 1 0] к целому числу 6. Блок производит тот же вывод, когда вход равняется 6, и параметром Input type является Integer.

Когда вы устанавливаете Constellation ordering (или Symbol set ordering или Symbol mapping) к Gray, блок использует серо-закодированное расположение и присваивает двоичные входы точкам предопределенного серо-закодированного сигнального созвездия. Предопределенное M-арное серо-закодированное сигнальное созвездие присваивает бинарное представление

M = 8; P = [0:M-1]';
de2bi(bitxor(P,floor(P/2)), log2(M),'left-msb')

к P ^th целое число.

Следующие таблицы показывают типичный Двоичный файл Серому отображению для M = 8.

Двоичный файл к серому отображению для битов

Двоичный код	Код Грея
000	000
001	001
010	011
011	010
100	110
101	111
110	101
111	100

Серый к двоичному отображению для Целых чисел

Двоичный код	Код Грея
0	0
1	1
2	3
3	2
4	6
5	7
6	5
7	4

Серое кодирование модулируемого сигнала

Скрипт Open Live Script

Для PSK, DPSK, FSK, QAM и типов модуляции PAM, совокупности Грэя получены путем установки отображения символа с серо-кодированием в соответствующей функции модуляции или Системе object®.

Для функций модуляции можно задать 'серый' для входного параметра порядка символа, чтобы получить серо-закодированную модуляцию.

Следующий пример использует функцию qammod с серо-закодированным отображением символа.

y = [0:15];
y = de2bi(y);
M = 16;
symorder = 'gray';
xmap = qammod(y,M,symorder,'InputType','bit','PlotConstellation',true);

Проверяя график совокупности, вы видите, что модулируемые символы серо-закодированы, потому что все смежные элементы отличаются только на один бит.

Сверхдискретизируйте изменения уровня и сигналы

Некоторые цифровые блоки модуляции могут вывести сверхдискретизированную версию модулируемого сигнала, в то время как их соответствующие цифровые блоки демодуляции могут принять сверхдискретизированную версию модулируемого сигнала, как введено. В обоих случаях параметр Rate options представляет фактор повышающей дискретизации, который должен быть положительным целым числом. В зависимости от того, является ли входной сигнал односкоростным режимом или многоскоростным режимом, блок или изменяет векторный размер сигнала или его шаг расчета, как следующая таблица указывает. Только блоки OQPSK отклоняются от информации в таблице, в которой S заменяется 2S в масштабных коэффициентах.

Обработайте сверхдискретизированные модулируемые данные (кроме метода OQPSK)

Тип вычисления	Введите состояние	Результат
Модуляция	Односкоростная обработка	Длина выходного вектора является временами S количество целых чисел или двоичных слов во входном векторе. Выходной шаг расчета равняется входному шагу расчета.
Модуляция	Многоскоростная обработка	Выходной вектор является скаляром. Выходной шаг расчета является 1/S временами входной шаг расчета.
Демодуляция	Односкоростная обработка	Количество целых чисел или двоичных слов в выходном векторе является 1/S временами количество выборок во входном векторе. Выходной шаг расчета равняется входному шагу расчета.
Демодуляция	Многоскоростная обработка	Выходной сигнал содержит одно целое число или одно двоичное слово. Выходной шаг расчета является временами S входной шаг расчета. Кроме того, если S> 1 и демодулятор от AM, PM или подбиблиотеки FM, демодулируемый сигнал задержан одним выходным демонстрационным периодом. Нет никакой задержки, если S = 1 или если демодулятор от подбиблиотеки CPM.

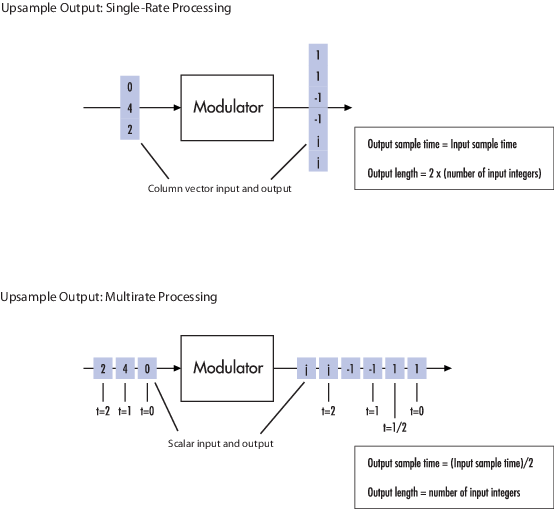
Рисунки Изменений Размера или Уровня. Следующая схематика иллюстрирует, как модулятор (кроме OQPSK) сверхдискретизировал триплет основанных на кадре и демонстрационных чисел с основанием. В обоих случаях параметром Samples per symbol является 2.

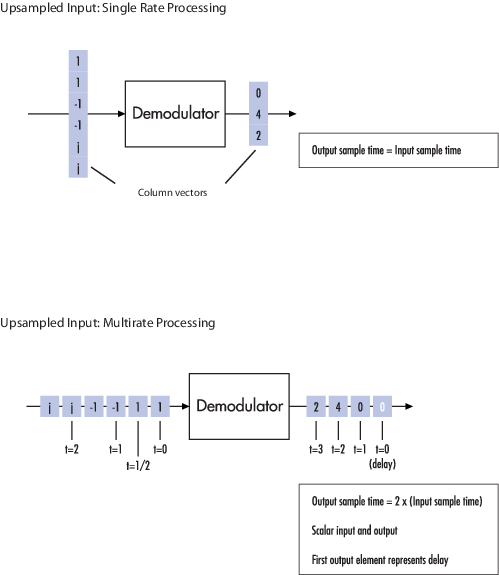
Следующая схематика иллюстрирует как демодулятор (кроме OQPSK или один от подбиблиотеки CPM) процессы три вдвойне выбранных символа с помощью и основанных на кадре и основанных на выборке входных параметров. В обоих случаях параметром Samples per symbol является 2. Основанное на выборке схематическое включает выходную задержку одного демонстрационного периода.

Для получения дополнительной информации о задержках смотрите Задержки Цифровой Модуляции.

Модуляция PM

Точки сигнального созвездия DQPSK и переходы

Модель ниже строит вывод блока DQPSK Modulator Baseband. Изображение показывает возможные переходы от каждого символа в сигнальном созвездии DQPSK к следующему символу.

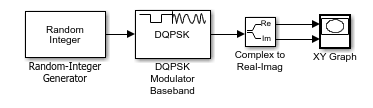
Чтобы открыть эту модель вводят doc_dqpsk_plot в командной строке MATLAB. Чтобы создать модель, соберите и сконфигурируйте эти блоки:

Случайный Целочисленный Генератор, в подбиблиотеке Random Data Sources библиотеки Comm Sources
- Установите M-ary number на 4.
- Установите Initial seed на любой положительный целочисленный скаляр, предпочтительно вывод функции randn.
- Установите Sample time на .01.
Основная полоса Модулятора DQPSK, в подбиблиотеке премьер-министра подбиблиотеки Digital Baseband Модуляции
Комплекс к Действительному-Imag, в библиотеке Simulink Math Operations
График XY, в библиотеке Simulink Sinks

Используйте параметры блоков по умолчанию, если в противном случае не проинструктировано. Соедините блоки как в фигуре выше. Выполнение модели производит следующий график. График отражает переходы среди восьми точек совокупности DQPSK.

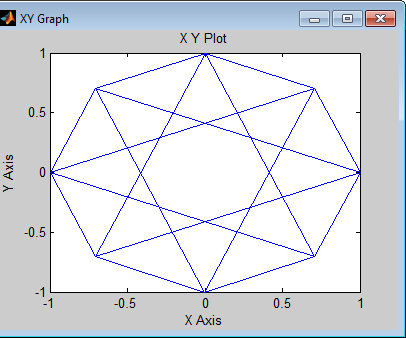
Этот график иллюстрирует π/4-DQPSK модуляцию, потому что параметром Phase offset по умолчанию в блоке DQPSK Modulator Baseband является pi/4. То, чтобы видеть, как фаза сместила, влияет на сигнальное созвездие, измените параметр Phase offset в блоке DQPSK Modulator Baseband к pi/8 или другому значению. Запустите модель снова и наблюдайте, как график изменяется.

Модуляция AM

Прямоугольная модуляция QAM и точечная диаграмма

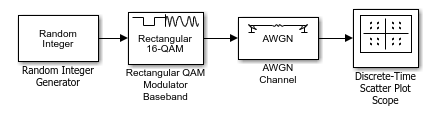
Модель ниже использует блок M-QAM Modulator Baseband, чтобы модулировать случайные данные. После передачи символов через шумный канал модель производит точечную диаграмму шумных данных. Схема предлагает то, на что базовое сигнальное созвездие похоже и показывает, что шум искажает модулируемый сигнал от совокупности.

Чтобы открыть эту модель, введите doc_qam_scatter в командной строке MATLAB. Чтобы создать модель, соберите и сконфигурируйте эти блоки:

Случайный Целочисленный Генератор, в подбиблиотеке Random Data Sources библиотеки Comm Sources
- Установите M-ary number на 16.
- Установите Initial seed на любой положительный целочисленный скаляр, предпочтительно вывод функции randn.
- Установите Sample time на .1.
Прямоугольная Основная полоса Модулятора QAM, в подбиблиотеке AM подбиблиотеки Digital Baseband Модуляции
- Установите Normalization method на Peak Power.
Канал AWGN, в библиотеке Channels
- Установите Es/No на 20.
- Установите Symbol period на .1.
Схема совокупности, в библиотеке Comm Sinks
- Установите Symbols to display на 160.

Соедините блоки как в фигуре. Из меню Simulation окна модели выберите Model Configuration parameters. В диалоговом окне Configuration Parameters, набор Stop time к 250. Выполнение модели производит точечную диаграмму как следующая. Ваш график может выглядеть несколько отличающимся, в зависимости от вашего значения Initial seed в блоке Random Integer Generator. Поскольку метод модуляции 16-QAM, график показывает 16 кластеров точек. Если бы не было никакого шума, график показал бы 16 точных точек совокупности вместо кластеров вокруг точек совокупности.

Вычислите коэффициент ошибок символа

Пример генерирует случайный цифровой сигнал, модулирует его и добавляет шум. Затем это создает график рассеивания, демодулирует сигнал с шумом и вычисляет коэффициент ошибок символа.

Вывод и график рассеивания следуют. Ваши числовые результаты и график могут отличаться, потому что пример использует случайные числа.

num =

    83


rt =

    0.0166

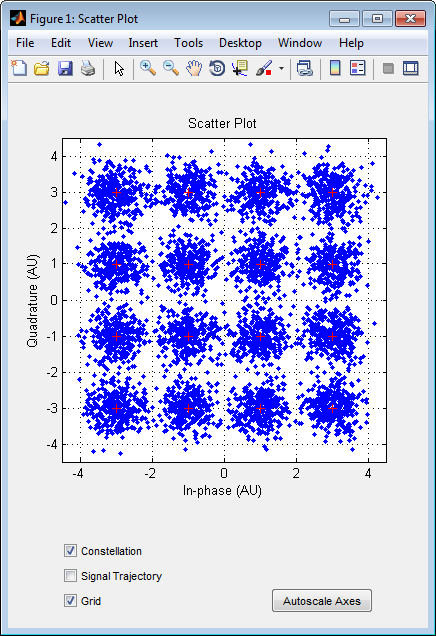
График рассеивания точно не походит на сигнальное созвездие. Где сигнальное созвездие имеет 16 точно расположенных точек, шум заставляет график рассеивания иметь небольшой кластер точек приблизительно, где каждая точка совокупности была бы.

Объедините импульсное формирование и фильтрацию с модуляцией

Модуляция часто сопровождается импульсным формированием, и демодуляции часто предшествуют фильтрация или операция интегрировать-и-выводить. Этот раздел представляет пример, включающий формирование меандра. Для примера, который использует повышенное формирование импульса косинуса, смотрите, что Импульс Формирует Используя Повышенный Фильтр Косинуса.

Формирование Меандра. Формирование меандра повторяет каждый вывод от модулятора постоянное число времен, чтобы создать сверхдискретизированный сигнал. Формирование меандра может быть первым шагом или исследовательским шагом в разработке алгоритмов, хотя это менее реалистично, чем другие виды импульсного формирования. Если передатчик сверхдискретизировал модулируемый сигнал, то получатель должен субдискретизировать полученный сигнал перед демодуляцией. “Интегрируют и выводят” операцию, один способ субдискретизировать полученный сигнал.

Код ниже использует функцию rectpulse для формирования меандра в передатчике и функцию intdump для субдискретизации в получателе.

M = 16;                     % Alphabet size, 16-QAM
x = randi([0 M-1],5000,1);  % Message signal
Nsamp = 4;                  % Oversampling rate

% Modulate
y = qammod(x,M);
% Follow with rectangular pulse shaping.
ypulse = rectpulse(y,Nsamp);

% Transmit signal through an AWGN channel.
ynoisy = awgn(ypulse,15,'measured');

% Downsample at the receiver.
ydownsamp = intdump(ynoisy,Nsamp);

% Demodulate to recover the message.
z = qamdemod(ydownsamp,M);

Модуляция CPM

Дерево фазы для непрерывной модуляции фазы

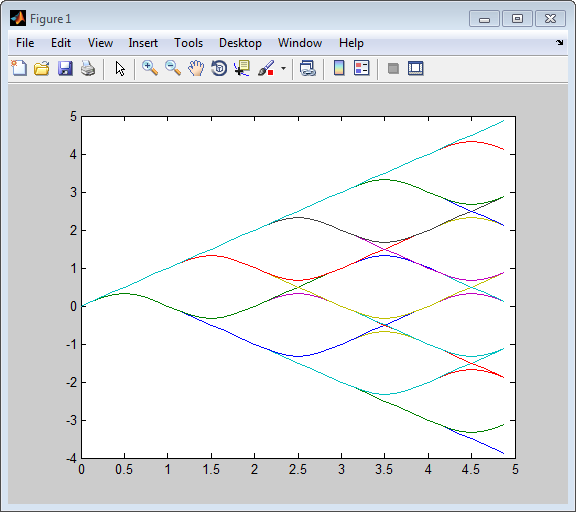
Этот пример строит дерево фазы, сопоставленное с непрерывной схемой модуляции фазы. Дерево фазы является схемой, которая накладывает много кривых, каждая из которых строит фазу модулируемого сигнала в зависимости от времени. Отличные кривые следуют из различных входных параметров к модулятору.

Этот пример использует блок CPM Modulator Baseband для своих численных расчетов. Блок сконфигурирован с помощью повышенной формы импульса фильтра косинуса. Пример также иллюстрирует, как можно использовать Simulink и MATLAB вместе. Пример использует команды MATLAB, чтобы запустить ряд симуляций с различными входными сигналами, собрать результаты симуляции и построить полный набор данных.

Примечание

В отличие от подхода этого примера с помощью и MATLAB и Simulink, пример commcpmphasetree производит дерево фазы использование модели Simulink без дополнительных строк кода MATLAB.

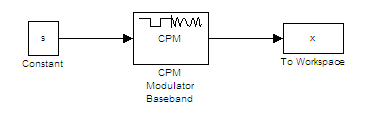
Откройте модель путем ввода doc_phasetree в командной строке MATLAB. Чтобы создать модель, соберите и сконфигурируйте эти блоки:

Постоянный, в библиотеке Simulink Commonly Used Blocks
- Установите Constant value на s (который появится в рабочем пространстве MATLAB).
- Установите Sampling mode на Frame-based.
- Установите Frame period на 1.
Основная полоса модулятора CPM
- Установите M-ary number на 2.
- Установите Modulation index на 2/3.
- Установите Frequency pulse shape на Raised Cosine.
- Установите Pulse length на 2.
К Рабочей области, в библиотеке Simulink Sinks
- Установите Variable name на x.
- Установите Save format на Array.

Не запускайте модель, потому что переменная s еще не задана в рабочем пространстве MATLAB. Вместо этого сохраните модель в папку на вашем пути MATLAB, с помощью имени файла doc_phasetree.

Второй шаг этого примера должен выполнить следующий код MATLAB:

% Parameters from the CPM Modulator Baseband block
M_ary_number = 2;
modulation_index = 2/3;
pulse_length = 2;
samples_per_symbol = 8;

L = 5;  % Symbols to display
pmat = [];
for ip_sig = 0:(M_ary_number^L)-1
    s = de2bi(ip_sig,L,M_ary_number,'left-msb');
    % Apply the mapping of the input symbol to the CPM
    % symbol 0 -> -(M-1), 1 -> -(M-2), etc.
    s = 2*s'+1-M_ary_number;
    sim('doc_phasetree', .9); % Run model to generate x.
    % Next column of pmat
    pmat(:,ip_sig+1) = unwrap(angle(x(:)));
end;
pmat = pmat/(pi*modulation_index);
t = (0:L*samples_per_symbol-1)'/samples_per_symbol;
plot(t,pmat); figure(gcf); % Plot phase tree.

Этот код задает параметры для Модулятора CPM, применяет отображение символа и строит результаты. Каждая кривая представляет различный экземпляр симуляции блока CPM Modulator Baseband с отличным (постоянным) входным сигналом.

Точный алгоритм LLR

Логарифмическое отношение правдоподобия (LLR) является логарифмом отношения вероятностей 0 битов, передаваемых по сравнению с 1 битом, передаваемым для полученного сигнала. LLR некоторое время b задан как:

$L (b) = журнал (\frac{PR (b = 0 | r = (x, y))}{PR (b = 1 | r = (x, y))})$

Принимая равную вероятность для всех символов, LLR для канала AWGN может быть выражен как:

$L (b) = журнал (\frac{\sum_{s \in S_{0}} e^{- \frac{1}{σ^{2}} ({(x - s_{x})}^{2} + {(y - s_{y})}^{2})}}{\sum_{s \in S_{1}} e^{- \frac{1}{σ^{2}} ({(x - s_{x})}^{2} + {(y - s_{y})}^{2})}})$

где переменные представляют значения, показанные в следующей таблице.

Переменная	Что представляет переменная
$r$	Полученный сигнал с координатами (x, y).
$b$	Переданный бит (один из битов K в M-арном символе, принимая все символы M одинаково вероятны.
$S_{0}$	Идеальные символы или совокупность указывают с битом 0 в данной позиции двоичного разряда.
$S_{1}$	Идеальные символы или совокупность указывают с битом 1 в данной позиции двоичного разряда.
$s_{x}$	Синфазная координата идеального символа или точки совокупности.
$s_{y}$	Квадратурная координата идеального символа или точки совокупности.
$σ^{2}$	Шумовое отклонение основополосного сигнала.
$σ_{x}^{2}$	Шумовое отклонение вдоль синфазной оси.
$σ_{y}^{2}$	Шумовое отклонение вдоль квадратурной оси.

Примечание

Шумовые компоненты вдоль синфазных осей и квадратурных осей приняты, чтобы быть независимыми и равной степени (т.е. $σ_{x}^{2} = σ_{y}^{2} = σ^{2} / 2$ ).

Аппроксимируйте алгоритм LLR

Аппроксимированный LLR вычисляется путем учета, что только самая близкая совокупность указывает на полученный сигнал с 0 (или 1) в той позиции двоичного разряда, а не всех точках совокупности, как сделано в точном LLR. Это задано как [8]:

$L (b) = - \frac{1}{σ^{2}} (\min_{s \in S_{0}} ({(x - s_{x})}^{2} + {(y - s_{y})}^{2}) - \min_{s \in S_{1}} ({(x - s_{x})}^{2} + {(y - s_{y})}^{2}))$

Задержки цифровой модуляции

Цифровые блоки модуляции и демодуляции иногда подвергаются задержкам между своими вводами и выводами, в зависимости от их настройки и на свойствах их сигналов. В следующей таблице перечислены источники задержки и ситуаций, в которых они происходят.

Задержки, следующие из цифровой модуляции или демодуляции

Модуляция или тип демодуляции	Ситуация, в которой происходит задержка	Сумма задержки
Демодулятор FM	Основанная на выборке обработка	Один выходной период
Все демодуляторы в подбиблиотеке CPM	Многоскоростная обработка и модель используют решатель переменного шага или решатель фиксированного шага с набором параметра Tasking Mode к `SingleTasking` D = параметр Traceback length	D+1 периоды вывода
Все демодуляторы в подбиблиотеке CPM	Односкоростная обработка, D = параметр Traceback depth	D периоды вывода
Демодулятор OQPSK	Односкоростная обработка	Для получения дополнительной информации см. Основную полосу Демодулятора OQPSK.
	Многоскоростная обработка и модель используют решатель фиксированного шага с набором параметра Tasking Mode к `Auto` или `MultiTasking`.
	Многоскоростная обработка обработки и модель используют решатель переменного шага, или параметр Tasking Mode устанавливается на Single`Tasking`.
Все декодеры в подбиблиотеке TCM	Набор Operation mode к `Continuous`, TR = параметр Traceback depth и уровень кода k/n	Tr*k биты вывода

В результате задержек данные, которые вводят блок модуляции или демодуляции во время T, появляются в выводе во время T+delay. В частности, если ваша симуляция вычисляет ошибочную статистику или соответствует переданный полученным данным, это должно принять задержку во внимание при выполнении таких вычислений или сравнений.

Сначала выведите выборку в демодуляции DPSK

В дополнение к упомянутым выше задержкам M-DPSK, DQPSK и демодуляторы DBPSK производят вывод, первая выборка которого не связана с входом. Это связано с дифференциальным методом модуляции, не конкретной реализацией его.

Пример: задержки от демодуляции

Демодуляция в модели ниже вызывает демодулируемый сигнал отстать, по сравнению с немодулируемым сигналом. Когда вычислительная ошибочная статистика, модель составляет задержку путем установки блока Error Rate Calculation параметр Receive delay на 0. Если бы параметр Receive delay имел различное значение, то показ коэффициента ошибок наверху блока Display был бы близко к 1/2.

Чтобы открыть эту модель, введите doc_oqpsk_modulation_delay в командной строке MATLAB. Чтобы создать модель, соберите и сконфигурируйте эти блоки:

Случайный Целочисленный Генератор, в подбиблиотеке Random Data Sources библиотеки Comm Sources
- Установите M-ary number на 4.
- Установите Initial seed на любой положительный целочисленный скаляр.
Основная полоса Модулятора OQPSK, в подбиблиотеке премьер-министра подбиблиотеки Digital Baseband Модуляции
Канал AWGN, в библиотеке Channels
- Установите Es/No на 6.
Основная полоса Демодулятора OQPSK, в подбиблиотеке премьер-министра подбиблиотеки Digital Baseband Модуляции
Вычисление Коэффициента ошибок, в библиотеке Comm Sinks
- Установите Receive delay на 1.
- Установите Computation delay на 0.
- Установите Output data на Port.
Отобразитесь в библиотеке Simulink Sinks
- Перетащите базовый край значка, чтобы сделать отображение достаточно большим для трех записей.

Соедините блоки как показано выше. От Simulation окна модели выберите Model Configuration parameters. В диалоговом окне Configuration Parameters, набор Stop time к 1000. Затем запустите модель и наблюдайте коэффициент ошибок наверху значка блока Display. Ваш коэффициент ошибок будет отличаться в зависимости от вашего значения Initial seed по блоку Random Integer Generator.

Выбранная библиография для цифровой модуляции

[1] Jeruchim, член конгресса, П. Балабан, и К. С. Шэнмугэн, симуляция Коммуникэйшн-Системс, Нью-Йорк, нажатия пленума, 1992.

[2] Proakis, J. G. Цифровая связь, 3-й редактор, Нью-Йорк, McGraw-Hill, 1995.

[3] Sklar, B., цифровая связь: основные принципы и приложения, Englewood Cliffs, NJ, Prentice Hall, 1988.

[4] Андерсон, J. B. Т. Олин и C.-E. Sundberg, цифровая модуляция фазы, Нью-Йорк, нажатие пленума, 1986.

[5] Biglieri, E., Д. Дивсэлэр, П.Дж. Маклэйн, и М.К. Саймон, введение в закодированную решеткой модуляцию с Аппликэйшнсом, Нью-Йорк, Макмиллана, 1991.

[6] Pawula, R.F., “На M-арной Передаче DPSK По Наземным и Спутниковым Каналам”, Транзакции IEEE на Коммуникациях, Издании COM-32, июль 1984, стр 752–761.

[7] Смит, J. G. “Нечетно-битное Квадратурное Манипулирование Амплитудного Сдвига”, Транзакции IEEE на Коммуникациях, Издании COM-23, март 1975, стр 385–389.

[8] Viterbi, A. J. “Интуитивное Выравнивание и Упрощенное внедрение Декодера MAP для Сверточных кодов”, Журнал IEEE на Выбранных областях в Коммуникациях, издании 16, № 2, стр 260–264, февраль 1998

Документация