dksyn

Устойчивое проектирование контроллера с помощью µ-synthesis

Синтаксис

[k,clp,bnd] = dksyn(p,nmeas,ncont)
[k,clp,bnd] = dksyn(p,nmeas,ncont,opt)
[k,clp,bnd,dkinfo] = dksyn(p,nmeas,ncont,...)
[k,clp,bnd,dkinfo] = dksyn(p,nmeas,ncont,prevdkinfo,opt)
 [...] = dksyn(p)

Описание

[k,clp,bnd] = dksyn(p,nmeas,ncont) синтезирует устойчивый контроллер k для неопределенной модели объекта управления разомкнутого цикла p через D-K или алгоритм D-G-K для µ-synthesis. p является неопределенной моделью uss пространства состояний. Последний nmeas выходные параметры and ncont вводят of p, принят, чтобы быть каналами измерения и управления. k является контроллером, clp является моделью с обратной связью, и bnd является устойчивой связанной производительностью с обратной связью. p, k, clp и bnd связаны можно следующим образом:

        clp = lft(p,k); 
        bnd1 = dksynperf(clp); 
        bnd = 1/bnd1.LowerBound;

[k,clp,bnd] = dksyn(p,nmeas,ncont,opt) задает пользовательские опции opt для алгоритма D-K-G или D-K. Используйте dksynOptions, чтобы создать opt.

[k,clp,bnd,dkinfo] = dksyn(p,nmeas,ncont,...) возвращается журнал осуществления алгоритма in dkinfo. dkinfo является N-by-1 массив ячеек, где N является общим количеством выполняемых итераций. i th ячейка содержит структуру со следующими полями:

Поле	Описание
`K`	Контроллер в `i` th итерация, объект `ss`
`Bnds`	Устойчивая производительность привязала систему с обратной связью (`double`)
`DL`	Оставленная D-шкала, объект `ss`
`DR`	Правильная D-шкала, объект `ss`
`GM`	Сместите G-шкалу, объект `ss`
`GR`	Правильная G-шкала, объект `ss`
`GFC`	Центральная G-шкала, объект `ss`
`MussvBnds`	Верхние и более низкие границы µ, объект `frd`
`MussvInfo`	Структура, возвращенная в `mussv` в каждой итерации.

[k,clp,bnd,dkinfo] = dksyn(p,nmeas,ncont,prevdkinfo,opt) allows you to use information from a previous dksyn iteration. prevdkinfo является структурой от предыдущей попытки разработки устойчивого контроллера, использующего dksyn. prevdkinfo используется, когда dksyn стартовая итерация не 1 (opt.StartingIterationNumber = 1), чтобы определить правильные D-масштабирования, чтобы инициировать процедуру итерации.

[...] = dksyn(p) берет p в качестве объекта uss, который имеет two-input/two-output, делящий, как задано mktito.

Примеры

Следующие операторы создают устойчивую систему управления производительности для нестабильной, неопределенной single-input/single-output модели объекта управления. Номинальная модель объекта управления, G, является нестабильной системой первого порядка $\frac{s}{s - 1}$ .

G = tf(1,[1 -1]);

Сама модель сомнительна. В низкой частоте, ниже 2 рад/с, это может отличаться до 25% от своей номинальной стоимости. Приблизительно 2 рад/с изменение процента начинает увеличиваться и достигает 400% на уровне приблизительно 32 рад/с. Неуверенность модели процента представлена весом Wu, который соответствует изменению частоты неуверенности модели и неопределенного динамического объекта LTI InputUnc.

Wu = 0.25*tf([1/2 1],[1/32 1]); 
InputUnc = ultidyn('InputUnc',[1 1]);

Неопределенная модель объекта управления Gpert представляет модель физической системы, которой будут управлять.

Gpert = G*(1+InputUnc*Wu);

Устойчивая цель устойчивости состоит в том, чтобы синтезировать стабилизировавшийся контроллер LTI для всех моделей объекта управления, параметризованных неопределенной моделью объекта управления, Gpert. Цель производительности задана как взвешенная проблема минимизации чувствительности. Структуру межсоединений управления показывают в следующей фигуре.

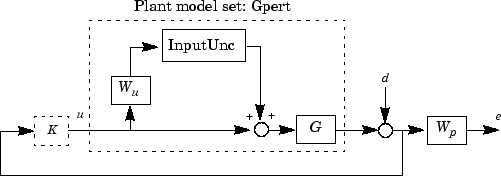
Функция чувствительности, S, задана как

$S = \frac{1}{1 + P K}$

где P является моделью объекта управления, и K является контроллером. Взвешенная проблема минимизации чувствительности выбирает вес Wp, который соответствует инверсии желаемой функции чувствительности системы с обратной связью как функция частоты. Следовательно продукт веса чувствительности Wp и фактическая функция чувствительности с обратной связью является меньше чем 1 через все частоты. Вес чувствительности Wp имеет усиление 100 в низкой частоте, начинает уменьшаться на уровне 0,006 рад/с и достигает минимального значения 0,25 после 2,4 рад/с.

Wp = tf([1/4 0.6],[1 0.006]);

Заданный Wp веса чувствительности подразумевает, что желаемое подавление помех должно быть, по крайней мере, 100:1 подавление помех в DC, медленно повышаться между 0.006 и 2,4 рад/с и позволять подавлению помех увеличиваться выше уровня разомкнутого цикла, 0.25, в высокой частоте.

Когда модель объекта управления сомнительна, цель производительности с обратной связью состоит в том, чтобы достигнуть желаемой функции чувствительности для всех моделей объекта управления, заданных неопределенной моделью объекта управления, Gpert. Цель производительности для неопределенной системы является устойчивой целью производительности. Блок-схему этой неопределенной системы с обратной связью, иллюстрирующей цель производительности (передаточная функция с обратной связью от d →e), показывают.

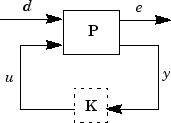
Из определения устойчивой цели управления производительностью взвешенная, неопределенная соединительная модель системы управления, которая включает робастность и цели производительности, может быть создана и обозначается P. Робастность и веса производительности выбраны таким образом, что, если устойчивое сингулярное значение структуры производительности, bnd, неопределенной системы с обратной связью, clp, является меньше чем 1 затем, цели производительности были достигнуты для всех моделей объекта управления в образцовом наборе.

Можно сформировать неопределенную матрицу передачи P от [d; u] до [e; y] с помощью следующих команд.

P = [Wp; 1 ]*[1 Gpert]; 
[K,clp,bnd] = dksyn(P,1,1); 
bnd

bnd = 
    0.6806

Контроллер K достигает устойчивой производительности µ значение bnd приблизительно 0,68. Поэтому вы достигли устойчивых целей производительности для данной проблемы.

Можно использовать команду robgain, чтобы анализировать устойчивую производительность с обратной связью clp.

[rpmarg,rpmargunc] = robgain(clp,1);

Ограничения

Существует два недостатка процедуры системы управления итерации D-K:

Вычисление структурированного сингулярного значения µΔ (·) аппроксимирован его верхней границей. Это не серьезная проблема, потому что значение µ и его верхней границы часто близко.
Итерация D-K, как гарантируют, не будет сходиться к глобальной переменной или даже локальному минимуму. Это - серьезная проблема и представляет самое большое ограничение методики проектирования.

Несмотря на эти недостатки, метод системы управления итерации D-K, кажется, работает хорошо над многими техническими проблемами. Это было применено ко многим реальным приложениям с успехом. Эти приложения включают подавление вибрации для гибких структур, управления полетом, химических проблем управления процессом и акустического подавления реверберации в корпусах.

Примеры

Управление Массового Демпфера Spring Используя Смешанный Mu-Synthesis

Алгоритмы

свернуть все

dksyn синтезирует устойчивый контроллер через итерацию D-K. Процедура итерации D-K является приближением к µ-synthesis системе управления. Цель µ-synthesis состоит в том, чтобы минимизировать сингулярное значение структуры µ соответствующей устойчивой проблемы производительности, сопоставленной с неопределенной системой p. Неопределенная система p является соединением разомкнутого цикла, содержащим известные компоненты включая номинальную модель объекта управления, неопределенные параметры, ucomplex, и несмоделированную динамику LTI, ultidyn, и функции взвешивания неуверенности и производительность. Вы используете функции взвешивания, чтобы включать информацию о формировании значения и частоты в оптимизацию. Цель управления состоит в том, чтобы синтезировать стабилизировавшийся контроллер k, который минимизирует устойчивую производительность µ значение, которое соответствует bnd.

Процедура итерации D-K включает последовательность минимизаций, сначала по переменной K контроллера (содержащий переменную D, сопоставленную с масштабированной µ зафиксированной верхней границей), и затем по переменной D (содержащий зафиксированную переменную K контроллера). Процедура итерации D-K, как гарантируют, не будет сходиться к минимуму µ значение, но часто работает хорошо на практике.

dksyn автоматизирует процедуру итерации D-K, и объект dksynOptions опций позволяет вам настраивать свое поведение. Внутренне, алгоритм работает с обобщенной масштабированной моделью объекта управления P, который извлечен от объекта uss с помощью команды lftdata.

Следующее является списком того, что происходит во время одного, полного шага итерации D-K.

(В первой итерации пропущен этот шаг.) µ вычисление (от предыдущего шага) обеспечивает зависимую частотой матрицу масштабирования, _Df. Подходящая процедура соответствует этим масштабированиям рациональными, стабильными матрицами передаточной функции. После подбора кривой, графиков
$\bar{σ} ({\hat{D}}_{f} (j ω) F_{L} (P, K) (j ω) D_{f}^{- 1} (j ω))$
и
$\bar{σ} ({\hat{D}}_{f} (j ω) F_{L} (P, K) (j ω) {\hat{D}}_{f}^{- 1} (j ω))$
показаны для сравнения.
(В первой итерации пропущен этот шаг.) Рациональное $\hat{D}$ поглощен в соединение разомкнутого цикла для следующего синтеза контроллера. Или Используя предыдущий зависимый частотой D' s или Используя рациональную справедливую подгонку $\hat{D}$ , оценка соответствующего значения для the H _∞ норма сделана. Это - просто консервативное значение масштабированного H с обратной связью _∞ norm, с помощью нового контроллера и любого развертка частоты (использующий зависимый частотой D' s) или вычисление пространства состояний (с рациональным D' s).
(Первая итерация начинается в этой точке.) Контроллер разработан с помощью H _∞ синтез на масштабированном соединении разомкнутого цикла. Если вы устанавливаете поле DisplayWhileAutoIter в dksynOptions к 'on', следующая информация отображена:
1. Прогресс γ - итерация отображен.
2. Сингулярные значения частотной характеристики с обратной связью построены.
3. Вам дают опцию, чтобы изменить частотный диапазон. Если вы изменяете его, все соответствующие частотные характеристики автоматически повторно вычисляются.
4. Вам дают опцию, чтобы повторно выполнить H _∞ синтез с набором измененных параметров, если вы устанавливаете поле AutoIter в dksynOptions к 'off'. Это удобно, если, например, допуск деления пополам был слишком большим, или если maximum gamma value был слишком маленьким.
Структурированное сингулярное значение системы с обратной связью вычислено и построено.
Сводные данные итерации отображены, показав весь порядок контроллера, а также пиковое значение µ частотных характеристик с обратной связью.
Выбор остановки или выполнения другой итерации дан.

Последующие итерации продолжают в том же направлении без потребности повторно войти в номер итерации. Сводные данные в конце каждой итерации обновляются, чтобы отразить данные из всех предыдущих итераций. Это часто предоставляет ценную информацию о прогрессе устойчивой процедуры синтеза контроллера.

Интерактивный подбор кривой D-масштабирований

Установка поля AutoIter в dksynOptions к 'off' требует, чтобы вы в интерактивном режиме соответствовали, D - масштабирует каждую итерацию. Во время шага 2 процедуры итерации D-K вам предлагают ввести ваш выбор опций для подбора кривой D - масштабирующиеся данные. Вы нажимаете, возвращаются после, следующее является списком ваших опций.

Enter Choice (return for list): 
  Choices:
		nd	Move to Next D-scaling
		nb	Move to Next D-Block
		i	Increment Fit Order
		d	Decrement Fit Order
		apf	Auto-PreFit
		mx 3	Change Max-Order to 3
		at 1.01	Change Auto-Prefit Tol to 1.01
		0	Fit with zeroth order
		2	Fit with second order
		n	Fit with n'th order
		e	Exit with Current Fittings
		s	See Status

nd и nb позволяют вам перемещаться от одного D - данные шкалы другому. nd перемещается в следующее масштабирование, тогда как nb перемещается в следующий блок масштабирования. Для скалярного D - масштабирования, это идентичные операции, но для проблем с полным D - масштабирования, (возмущения формы δI) они отличаются. В (1,2) окно подграфика, заголовок отображает D - масштабирующий номер блока, строку/столбец масштабирования, которое в настоящее время адаптируется, и порядок текущей подгонки (с d для данных, когда никакая подгонка не существует).
Можно постепенно увеличить или постепенно уменьшить порядок текущей подгонки (1) использование i и d.
apf автоматически соответствует каждому D - масштабирующиеся данные. Максимальный порядок состояний по умолчанию отдельного D - масштабирование равняется 5. Переменная mx позволяет вам изменять максимальный D - масштабирующий порядок состояний, используемый в автоматической предподходящей стандартной программе. mx должен быть положительным, ненулевым целым числом. at позволяет вам задавать, как близко рациональное, масштабированная µ верхняя граница должна аппроксимировать фактическую µ верхнюю границу в смысле нормы. Установка at to 1 потребовала бы точного припадка D - данные шкалы и не позволена. Допустимые значения для at больше, чем 1. Эта установка играет роль (мягко непредсказуемый, к сожалению) в определении, где в (D, K) располагают итерацию D-K с интервалами, сходится.
Ввод положительного целого числа в подсказке будет соответствовать текущему D - данные шкалы с тем порядком состояний рациональная передаточная функция.
e выходит из D - шкала, соответствующая, чтобы продолжить итерацию D-K.
Переменная s отображает состояние тока и подгонок.

Ссылки

[1] Прозрачная шпинель, G.J., и Дж.К. Дойл, “Устойчивое управление гибких режимов в контроллере перекрестно соединяет область”, Журнал AIAA Руководства, Динамики и Управления, Издания 17, № 2, март-апрель 1994, p. 370-377.

[2] Прозрачная шпинель, G.J., А.К. Пэкард и Дж.Т. Хардувель, “Приложение µ-synthesis методов к административному управлению импульса и управлению ориентацией космической станции”, Руководство AIAA, Навигация и Конференция по Управлению, Новый Орлеан, август 1991.

[3] Дойл, J.C., К. Ленц и А. Пэкард, “Примеры проекта с помощью µ-synthesis: FCS оси ответвления Шаттла во время возвращения”, Ряд ASI НАТО, Моделирование, Робастность и Сокращение Чувствительности Систем управления, издания 34, Springer-Verlag, Берлина 1987.

[4] Паккард, A., Дж. Дойл и Г. Бэлас, “Линейное, многомерное устойчивое управление с µ перспективой”, Журнал ASME Динамических систем, Измерения и Управления, 50-го Ежегодного Выпуска, Издания 115, № 2b, июнь 1993, p. 310-319.

[5] Глиняная кружка, G. и Дж. Дойл, “Вне сингулярных значений и loopshapes”, Журнал AIAA Руководства и Управления, Издания 14, № 1, январь 1991, p. 5-16.

Документация

dksyn

Синтаксис

Описание

Примеры

Ограничения

Примеры

Алгоритмы

Интерактивный подбор кривой D-масштабирований

Ссылки

Смотрите также

Представлено до R2006a

Документация Robust Control Toolbox

Поддержка