erfiМнимая функция ошибок
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
erfi(x)
вычисляет мнимую функцию ошибок.
Эта функция задана для всех сложных аргументов x. Для аргументов с плавающей точкой erfi возвращает результаты с плавающей точкой.
Реализованные точные значения: erfi(0) = 0, erfi(∞) = ∞, erfi(-∞) = -∞, erfi(i∞) = i и erfi(-i∞) = -i. Для всех других аргументов функция ошибок возвращает символьные вызовы функции.
Для вызова функции может произойти erfi(x) = -i*erf(i*x) = i*(erfc(i*x) - 1) с аргументами с плавающей точкой большого абсолютного значения, внутренней числовой потери значимости или переполнения. Если вызов потери значимости причин erfc или переполнения, эта функция возвращается:
Результат, усеченный к 0.0, если x является большим положительным вещественным числом
Результат округлился к 2.0, если x является большим отрицательным вещественным числом
RD_NAN, если x является большим комплексным числом и MuPAD®, не может аппроксимировать значение функции
Мнимая функция ошибок erfi(x) = i*(erfc(i*x) - 1) возвращает соответствующие значения для больших аргументов. Смотрите Пример 2.
MuPAD может упростить выражения, которые содержат функции ошибок и их инверсии. Для действительных значений x система применяет следующие правила упрощения:
inverf(erf(x)) = inverf(1 - erfc(x)) = inverfc(1 - erf(x)) = inverfc(erfc(x)) = x
inverf(-erf(x)) = inverf(erfc(x) - 1) = inverfc(1 + erf(x)) = inverfc(2 - erfc(x)) = -x
Для любого значения x система применяет следующие правила упрощения:
inverf(-x) = -inverf(x)
inverfc(2 - x) = -inverfc(x)
erf(inverf(x)) = erfc(inverfc(x)) = x
erf(inverfc(x)) = erfc(inverf(x)) = 1 - x
Когда названо аргументом с плавающей точкой, функции чувствительны к переменной окружения DIGITS, который определяет числовую рабочую точность.
Можно вызвать мнимую функцию ошибок с точными и символьными аргументами:
erfi(0), erfi(x + 1), erfi(-infinity), erfi(3/2), erfi(sqrt(2))
![]()
Чтобы аппроксимировать точные результаты с числами с плавающей запятой, используйте float:
float(erfi(3/2)), float(erfi(sqrt(2)))
![]()
Также используйте значение плавающих точек в качестве аргументов:
erfi(0.2), erfi(2.0 + 3.5*I), erfi(5.5 + 1.0*I)
![]()
Для больших сложных аргументов может возвратиться мнимая функция ошибок![]() :
:
erfi(38000.0 + 3801.0*I)
![]()
diff, float, limit, expand, rewrite и series обрабатывают выражения, включающие функции ошибок:
diff(erfi(x), x, x, x)

float(ln(3 + erfi(sqrt(PI)*I)))
![]()
limit(x/(1 + x)*erfi(I*x)*I, x = infinity)
![]()
rewrite(erfi(x), erfc)
![]()
series(erfi(x), x = I*infinity, 3)
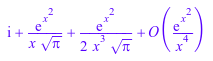
|
Арифметическое выражение
erf, erfc и erfi являются целыми функциями.