график::Поверхности в 3D, параметризованном в цилиндрических координатах
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
plot::Cylindrical([r, ϕ, z], u = umin .. umax, v = vmin .. vmax, <a = amin .. amax>, options)
plot::Cylindrical создает поверхности, параметризованные в цилиндрических координатах.
Поверхность, данная отображением (“параметризация”)![]() , является набором всех точек изображений
, является набором всех точек изображений
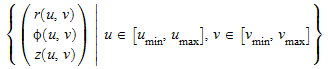
в цилиндрических координатах, которые переводят в обычные “Декартовы” координаты как
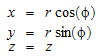 .
.
r упоминается как “радиус”, ϕ как “угол в полярных координатах” и z как “высота” точки.
Функции r, ϕ, z оценен на регулярной равноотстоящей mesh точек выборки в u-v плоскость. Эта mesh определяется атрибутами UMesh, VMesh. По умолчанию атрибут, AdaptiveMesh = 0 установлен, т.е. никакое адаптивное улучшение равноотстоящей mesh, используется.
Если стандартная mesh не достаточна, чтобы произвести достаточно подробный график, можно или увеличить значение UMesh, VMesh или USubmesh, VSubmesh, или установить AdaptiveMesh = n с некоторым (маленьким) положительным целочисленным n. При необходимости до 2n - 1 дополнительная точка помещается в каждое направление u-v плоскость между смежными точками начальной равноотстоящей mesh. Cf. Пример 2.
“Координатные строки” (“строки параметра”) являются кривыми на поверхности.
Фраза “ULines” отсылает к кривым (r (u, v 0), ϕ (u, v 0), z (u, v 0)) с параметром u, запускающийся от umin до umax, в то время как v 0 является некоторым фиксированным значением от интервала [vmin, vmax].
Фраза “VLines” отсылает к кривым (r (u 0, v), ϕ (u 0, v), z (u 0, v)) с параметром v, запускающийся от vmin до vmax, в то время как u 0 является некоторым фиксированным значением от интервала [umin, umax].
По умолчанию кривые параметра видимы. Они могут быть выключены путем определения ULinesVisible = FALSE и VLinesVisible = FALSE, соответственно.
Координатные строки, которыми управляет ULinesVisible = TRUE/FALSE и VLinesVisible = TRUE/FALSE, указывают на равноотстоящую mesh в u-v плоский набор через UMesh, атрибуты VMesh. Если mesh усовершенствована USubmesh, атрибутами VSubmesh, или адаптивным механизмом, которым управляет AdaptiveMesh = n, никакие дополнительные линии параметра не проведены.
Насколько числовое приближение поверхности затронуто, настройки
UMesh = nu, VMesh = nv, USubmesh = mu, VSubmesh = mv
и
UMesh = (nu - 1) (mu + 1) + 1, VMesh = (nv - 1) (mv + 1) + 1,
USubmesh = 0, VSubmesh = 0
эквивалентны. Однако в первой установке, строки параметра nu видимы в направлении u, в то время как в последнем параметре установки (nu - 1) (mu + 1) + 1 строки видимы. Cf. Пример 2.
Используйте Filled = FALSE, чтобы получить каркасное представление поверхности.
Если выражения/функции, r и/или z содержат особенности, это рекомендуется (но не строго необходимое), чтобы использовать атрибут ViewingBox, чтобы установить подходящее поле просмотра. Никакие такие меры предосторожности не необходимы для ϕ, несмотря на то, что особенности в этой функции могут привести к плохо представленным поверхностям – во многих случаях установка атрибутов, Mesh и/или AdaptiveMesh к более высоким значениям помогут. Cf. Пример 3.
| Атрибут | Цель | Значение по умолчанию |
|---|---|---|
AdaptiveMesh | адаптивная выборка | 0 |
AffectViewingBox | влияние объектов на ViewingBox сцены | TRUE |
Color | основной цвет | RGB::Red |
Filled | заполненные или прозрачные области и поверхности | TRUE |
FillColor | цвет областей и поверхностей | RGB::Red |
FillColor2 | второй цвет областей и поверхностей для цветных смешений | RGB::CornflowerBlue |
FillColorType | типы заполнения поверхности | Dichromatic |
FillColorFunction | функциональная область / поверхностная окраска | |
FillColorDirection | направление цветовых переходов на поверхностях | [0, 0, 1] |
FillColorDirectionX | x-компонент направления цветовых переходов на поверхностях | 0 |
FillColorDirectionY | y-компонент направления цветовых переходов на поверхностях | 0 |
FillColorDirectionZ | z-компонент направления цветовых переходов на поверхностях | 1 |
Frames | количество кадров в анимации | 50 |
Legend | делает запись легенды | |
LegendText | короткий объяснительный текст для легенды | |
LegendEntry | добавить этот объект в легенду? | TRUE |
LineColor | цвет строк | RGB::Black.[0.25] |
LineWidth | ширина строк | 0.35 |
LineColor2 | цвет строк | RGB::DeepPink |
LineStyle | тело, подчеркнутые штриховой линией или пунктирные линии? | Solid |
LineColorType | типы окраски строки | Flat |
LineColorFunction | функциональная окраска строки | |
LineColorDirection | направление цветовых переходов на строках | [0, 0, 1] |
LineColorDirectionX | x-компонент направления цветовых переходов на строках | 0 |
LineColorDirectionY | y-компонент направления цветовых переходов на строках | 0 |
LineColorDirectionZ | z-компонент направления цветовых переходов на строках | 1 |
Mesh | количество точек выборки | [25, 25] |
MeshVisible | видимость неправильных строк mesh в 3D | FALSE |
Name | имя объекта графика (для браузера и легенды) | |
ParameterEnd | закончите значение параметра анимации | |
ParameterName | имя параметра анимации | |
ParameterBegin | начальное значение параметра анимации | |
ParameterRange | область значений параметра анимации | |
PointSize | размер точек | 1.5 |
PointStyle | стиль презентации точек | FilledCircles |
PointsVisible | видимость точек mesh | FALSE |
Submesh | плотность подmesh (дополнительные точки выборки) | [0, 0] |
TimeEnd | время окончания анимации | 10.0 |
TimeBegin | время начала анимации | 0.0 |
TimeRange | оперативный промежуток анимации | 0.0 .. 10.0 |
Title | объектный заголовок | |
TitleFont | шрифт объектных заголовков | [" sans-serif ", 11] |
TitlePosition | положение объектных заголовков | |
TitleAlignment | выравнивание по горизонтали заголовков w.r.t. их координаты | Center |
TitlePositionX | положение объектных заголовков, x компонент | |
TitlePositionY | положение объектных заголовков, y компонент | |
TitlePositionZ | положение объектных заголовков, z компонент | |
ULinesVisible | видимость строк параметра (u строки) | TRUE |
UMax | окончательное значение параметра “u” | |
UMesh | количество точек выборки для параметра “u” | 25 |
UMin | начальное значение параметра “u” | |
UName | имя параметра “u” | |
URange | область значений параметра “u” | |
USubmesh | плотность дополнительных точек выборки для параметра “u” | 0 |
VLinesVisible | видимость строк параметра (v строки) | TRUE |
VMax | окончательное значение параметра “v” | |
VMesh | количество точек выборки для параметра “v” | 25 |
VMin | начальное значение параметра “v” | |
VName | имя параметра “v” | |
VRange | область значений параметра “v” | |
VSubmesh | плотность дополнительных точек выборки для параметра “v” | 0 |
Visible | видимость | TRUE |
VisibleAfter | объект, видимый после этой временной стоимости | |
VisibleBefore | объект, видимый до этой временной стоимости | |
VisibleFromTo | объект, видимый в это время, располагается | |
VisibleAfterEnd | объект, видимый после его законченного времени анимации? | TRUE |
VisibleBeforeBegin | объект, видимый перед его временем анимации, запускается? | TRUE |
XContours | линии контура в постоянных x значениях | [] |
XFunction | функция для x значений | |
YContours | линии контура в постоянных y значениях | [] |
YFunction | функция для y значений | |
ZContours | линии контура в постоянных z значениях | [] |
ZFunction | функция для z значений |
Используя постоянный радиус для plot::Cylindrical, с другими двумя функциями прямо от поверхностных параметров, результатов в правильном цилиндре. Это объясняет имя “цилиндрические координаты”:
plot(plot::Cylindrical([1, phi, z], phi = 0..2*PI, z = -1..1))
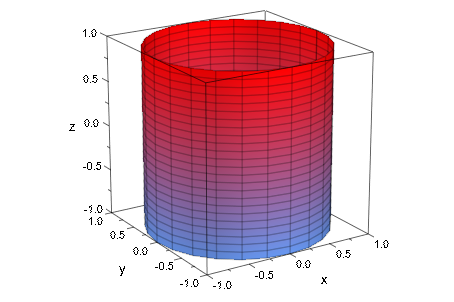
Другие прямые примеры включают конусы и параболоиды оборота:
plot(plot::Cylindrical([r, phi, 2*r], r = 0..1, phi = 0..2*PI))
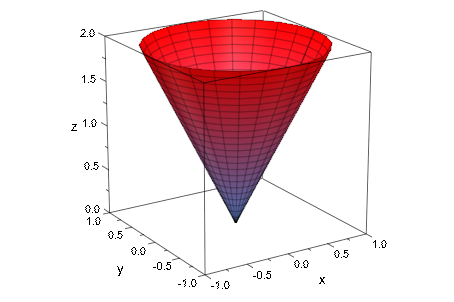
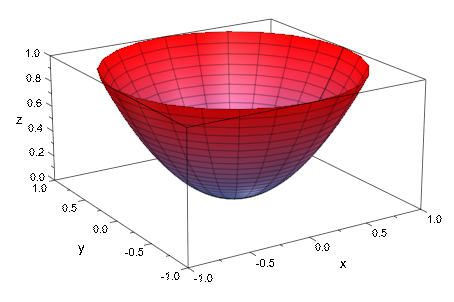
plot(plot::Cylindrical([r, phi, r^2], r = 0..1, phi = 0..2*PI))
Цилиндрические поверхности чертятся от оценок на равноотстоящей сетке точек. В некоторых случаях плотность mesh по умолчанию является недостаточной или в противном случае несоответствующей:
plot(plot::Cylindrical([cos(phi^2), phi, z],
phi=-2.8..2.8, z=0..1/2))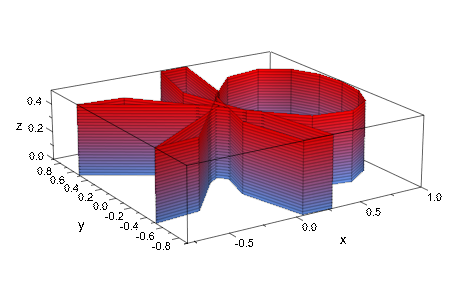
Одно возможное изменение в этой команде plot должно явным образом установить mesh с атрибутом Mesh. Обратите внимание на то, что эта установка влияет на плотность строк параметра:
plot(plot::Cylindrical([cos(phi^2), phi, z],
phi=-2.8..2.8, z=0..1/2,
Mesh = [100, 5]))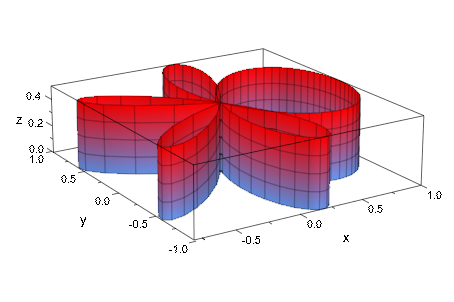
Чтобы повысить плотность mesh, не вводя дополнительные строки параметра, можно использовать настройки подmesh:
plot(plot::Cylindrical([cos(phi^2), phi, z],
phi=-2.8..2.8, z=0..1/2,
VMesh = 5, USubmesh = 3))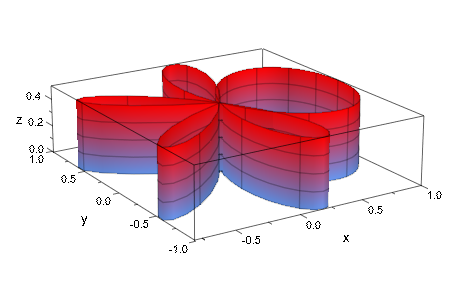
Наконец, мы можем также попросить, чтобы plot::Cylindrical совершенствовал mesh только в областях высшей кривизны. В следующем примере мы допускаем 23 = 8 дополнительных точек между каждым две соседних точки начальной mesh:
plot(plot::Cylindrical([cos(phi^2), phi, z],
phi=-2.8..2.8, z=0..1/2,
VMesh = 5, AdaptiveMesh = 3))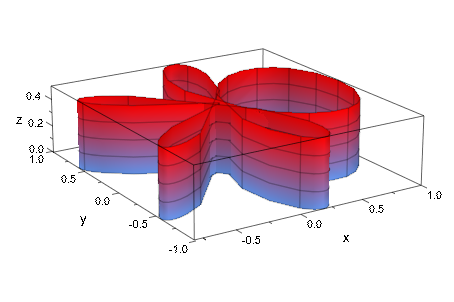
Если радиус - или z-function/expression содержит особенности, plot::Cylindrical использует усечение эвристики, чтобы выбрать область значений, чтобы отобразиться:
plot(plot::Cylindrical([1/sqrt((phi - PI)^2 + z^2), phi, z],
phi = 0..2*PI, z = -1..1))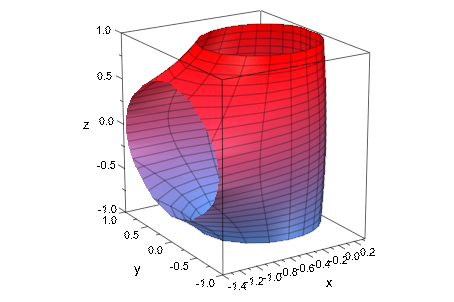
В то время как эта эвристика работает хорошо во многих случаях, существуют также примеры, где они не выбирают полезное поле:
plot(plot::Cylindrical([1/((phi - PI)^2 + z^2), phi, z],
phi = 0.. 2*PI, z = -1..1))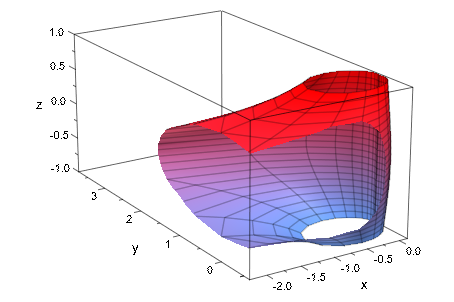
В этих случаях пользователь должен установить область значений отображаться явным образом:
plot(plot::Cylindrical([1/((phi - PI)^2+z^2), phi, z],
phi = 0..2*PI, z = -1..1),
ViewingBox = [-2..0.3, -1.5..1.5, -1..1])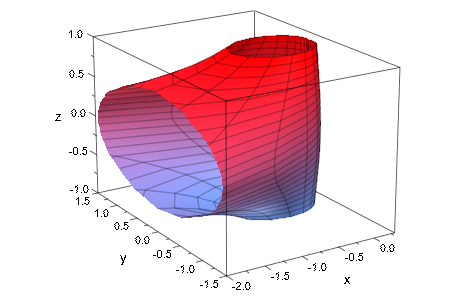
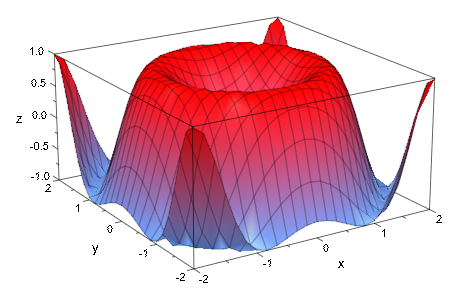
Поскольку преобразование от цилиндрического до прямоугольных координат обратимо (до сокращения угла к области значений [0, 2 π], возможно построить любую поверхность с plot::Cylindrical (несмотря на то, что это - вероятно, больше любопытство, чем действительно полезный):
trans := linalg::ogCoordTab[Cylindrical, InverseTransformation]: cyl := trans(x, y, sin(x^2+y^2))

plot(plot::Cylindrical(cyl, x = -2..2, y = -2..2))
|
Координатные функции: арифметические выражения или
|
|
Первый поверхностный параметр: идентификатор или индексируемый идентификатор. |
|
Область значений графика для параметра u: |
|
Второй поверхностный параметр: идентификатор или индексируемый идентификатор.
|
|
Область значений графика для параметра v: |
|
Параметр анимации, заданный как |