Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
В предыдущем разделе мы ввели plotfunc2d и plotfunc3d, которые служат для функций построения графика в 2D и 3D с простыми вызовами в легком синтаксисе. Несмотря на то, что все атрибуты графика, принятые функциональными графиками (типа plot::Function2d или plot::Function3d, соответственно), также приняты plotfunc2d/3d, там остается серьезное ограничение: атрибуты используются для всех функций одновременно.
Если атрибуты должны быть применены к функциям индивидуально, нужно вызвать (немного) более тщательно продуманный синтаксис вызова, чтобы сгенерировать график:
plot( plot::Function2d(f1, x1 = a1..b1, attrib11, attrib12, ...), plot::Function2d(f2, x2 = a2..b2, attrib21, attrib22, ...), ... ):
В этом вызове каждый вызов plot::Function2d создает отдельный объект, который представляет график функции, переданной в качестве первого аргумента в области значений графического вывода, переданной в качестве второго аргумента. Произвольное число атрибутов графика может быть сопоставлено с каждым функциональным графиком. Сами объекты не отображены непосредственно. Команда plot инициировала оценку функций на некоторой подходящей числовой mesh и вызывает средство отображения, чтобы отобразить эти числовые данные в форме, заданной данными атрибутами.
На самом деле plotfunc2d и plotfunc3d делают точно то же самое: Внутренне, они генерируют объекты графика типа plot::Function2d или plot::Function3d, соответственно, и вызывают средство отображения через plot.
В целом графические сцены являются наборами “графических примитивов”. Существуют простые примитивы, такие как точки, линейные сегменты, полигоны, прямоугольники и поля, круги и сферы, графики гистограммы, круговые диаграммы и т.д. Примером более усовершенствованного примитива является plot::VectorField2d, который представляет набор стрелок, присоединенных к регулярной mesh, визуализирующей векторное поле по прямоугольной области в ℝ 2. Все же более усовершенствованные примитивы являются функциональными графиками и параметризованными кривыми, к которым прилагается некоторый внутренний интеллект, например, зная, как оценить себя численно на адаптивных сетках и как отсечь себя в случае особенностей. Самыми усовершенствованными примитивами в существующей библиотеке plot является plot::Ode2d, plot::Ode3d и plot::Implicit2d, plot::Implicit3d. Первые автоматически решают системы обыкновенных дифференциальных уравнений численно и отображают решения графически. Последнее отображение кривые решения или поверхности алгебраических уравнений f (x, y) = 0 или f (x, y, z) = 0, соответственно, путем решения их уравнение численно.
Все эти примитивы являются только “объектами”, представляющими некоторые графические сущности. Они не представляются непосредственно, когда они создаются, но только служат структурами данных, кодирующими графическое значение, сбор атрибутов, задающих стиль презентации и обеспечивающих числовые стандартные программы, чтобы преобразовать входные параметры в некоторые числовые данные, которые должны быть отправлены в средство отображения.
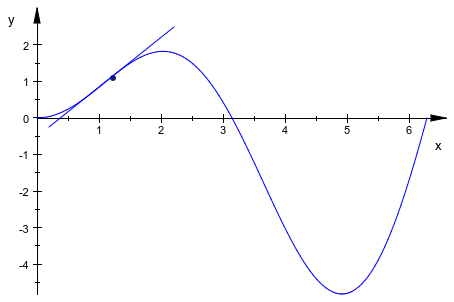
Произвольное число таких примитивов может быть собрано, чтобы сформировать графическую сцену. Наконец, вызов plot, передающего последовательность всех примитивов в сцене, вызывает средство отображения, чтобы построить график. Следующий пример показывает график функционального f (x) = x sin (x). В точке (x 0, f (x 0)), вставляется графическая точка, и касательная к графику через эту точку добавляется:
f := x -> x*sin(x):
x0 := 1.2: dx := 1:
g := plot::Function2d(f(x), x = 0..2*PI):
p := plot::Point2d(x0, f(x0)):
t := plot::Line2d([x0 - dx, f(x0) - f'(x0)*dx],
[x0 + dx, f(x0) + f'(x0)*dx]):Изображение нарисовано путем вызова plot:
plot(g, p, t):
Каждый примитив принимает множество атрибутов графика, которые могут быть переданы как последовательность уравнений AttributeName = AttributeValue к генерирующемуся вызову. Наиболее заметно каждый примитив позволяет выбирать цвет явным образом:
g := plot::Function2d(f(x), x = 0..2*PI, Color = RGB::Blue):
Также сгенерированные объекты позволяют устанавливать атрибуты через назначения слотов формы primitive::AttributeName := AttributeValue как в
p::Color := RGB::Black: p::PointSize := 3.0*unit::mm: t::Color := RGB::Red: t::LineWidth := 1.0*unit::mm:
Страница справки каждого примитива предоставляет список всех атрибутов, на которые реагирует примитив.
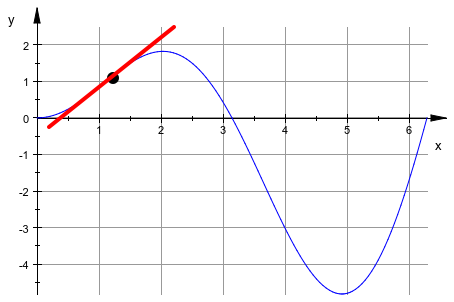
Определенные атрибуты, такие как оси разрабатывают, видимость линий сетки в фоновом режиме и т.д. сопоставлены с целой сценой, а не с отдельными примитивами. Эти атрибуты могут быть включены в вызов plot:
plot(g, p, t, GridVisible = TRUE):
Как объяснено подробно в разделе The Full Picture: Графические Деревья, команда plot автоматически встраивает графические примитивы в систему координат, которая в свою очередь встраивается в графическую сцену, которая чертится в холсте. Различные атрибуты, сопоставленные с общим видом целого изображения, сопоставлены с этими “структурами группировки”: краткий список всех таких атрибутов предоставлен на страницах справки plot::Canvas, plot::Scene2d, plot::Scene3d, plot::CoordinateSystem2d и plot::CoordinateSystem3d, соответственно.
Обозреватель объектов, обеспеченный инструментом графики MuPAD®, позволяет выбирать каждый примитив в графике. После выбора атрибуты примитива могут быть изменены в интерактивном режиме в инспекторе свойств (см. раздел Viewer, Браузер и Инспектора: Интерактивная Манипуляция).
Затем, мы хотим продемонстрировать анимацию. Удивительно просто сгенерировать изображение с анимацией. Мы хотим позволить точке x 0, в котором добавляется касательная, проходят график функции. В MuPAD вы не должны создавать кадр анимации кадром. Вместо этого каждому примитиву можно сказать анимировать себя путем простого определения его с символьным параметром анимации и добавления области значений анимации для этого параметра. Статические и анимированные объекты могут быть смешаны и представлены вместе. Статический функциональный график f (x), используемый в предыдущем графике, переработан для анимации. Графическая точка в (x 0, f (x 0)) и касательная через эту точку должна быть анимирована с помощью координатного x0 в качестве параметра анимации. Удаляя его набор значений выше, мы можем использовать те же определения как прежде, теперь с символьным x0. Мы только должны добавить спецификацию области значений x0 = 0..2*PI для этого параметра:
delete x0:
dx := 2/sqrt(1 + f'(x0)^2):
p := plot::Point2d(x0, f(x0), x0 = 0..2*PI,
Color = RGB::Black,
PointSize = 2.0*unit::mm):
t := plot::Line2d([x0 - dx, f(x0) - f'(x0)*dx],
[x0 + dx, f(x0) + f'(x0)*dx],
x0 = 0..2*PI, Color = RGB::Red,
LineWidth = 1.0*unit::mm):
plot(g, p, t, GridVisible = TRUE):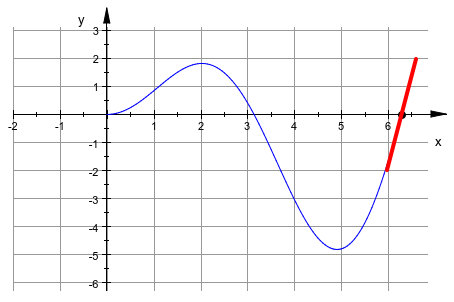
Подробная информация об анимациях и дальнейших примерах предоставлена в разделе Graphics и Animations.
Мы обобщаем принципы конструкции для графики с библиотекой MuPAD plot:
Графические сцены создаются из графических примитивов. Разделите Графику, и Анимации предоставляет обзор примитивов, которые доступны в библиотеке plot.
Примитивы, сгенерированные библиотекой plot, являются символьными объектами, которые не представляются непосредственно. Вызов plot(Primitive1, Primitive2, ...) генерирует изображения.
Графические атрибуты заданы как уравнения AttributeName = AttributeValue. Атрибуты для графического примитива могут быть переданы в вызове, который генерирует примитив. Страница справки каждого примитива предоставляет полный список всех атрибутов, на которые реагирует примитив.
Атрибуты, определяющие общий вид изображения, могут быть переданы в вызове plot. Страницы справки plot::Canvas, plot::Scene2d, plot::Scene3d, plot::CoordinateSystem2d, и plot::CoordinateSystem3d, соответственно, предоставляют полный список всех атрибутов, определяющих общий вид.
Все атрибуты могут быть изменены в интерактивном режиме в средстве просмотра.
В настоящее время 2D и 3D графики строго разделяются. Объекты различной размерности не могут быть представлены в том же графике.
Анимации не создаются кадр кадром, но objectwise (также смотрите раздел Frame by Frame Animations). Объект анимирован путем генерации его с символьным параметром анимации и предоставления спектра для этого параметра в генерирующемся вызове. Разделите Графику, и Анимации предусматривает более подробную информацию об анимациях.
В настоящее время не возможно добавить объекты в существующий график. Однако с помощью анимаций, возможно позволить примитивам появиться один за другим на изображении с анимацией. Смотрите Графику и Анимации.
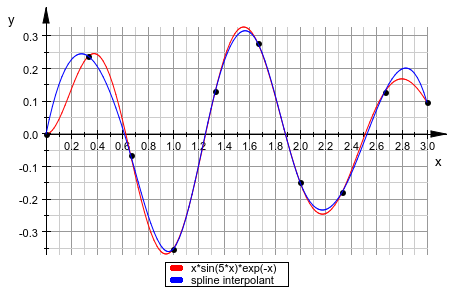
Мы хотим визуализировать интерполяцию выборки дискретных данных кубическими сплайнами. Во-первых, мы задаем выборку данных, состоя из списка точек [[x 1, y 1], [x 2, y 2], …]. Предположим, что они - равноотстоящие точки выборки из графика функции![]() :
:
f := x -> x*exp(-x)*sin(5*x): data := [[i/3, f(i/3)] $ i = 0..9]:
Мы используем numeric::cubicSpline, чтобы задать кубический сплайн interpolant через эти данные:
S := numeric::cubicSpline(op(data)):
График должен состоять из функционального f (x), который обеспечивает данные точек выборки и сплайна interpolant S (x). Графики f (x) и S (x) сгенерированы через plot::Function2d. Точки данных построены как plot::PointList2d:
plot(
plot::Function2d(f(x), x = 0..3, Color = RGB::Red,
LegendText = expr2text(f(x))),
plot::PointList2d(data, Color = RGB::Black),
plot::Function2d(S(x), x = 0..3, Color = RGB::Blue,
LegendText = "spline interpolant"),
GridVisible = TRUE, SubgridVisible = TRUE,
LegendVisible = TRUE
):
Циклоида является кривой, которую вы получаете при следовании за точкой, зафиксированной к колесу, едущему по прямой линии. Мы визуализируем эту конструкцию анимацией, в которой мы используем координату x концентратора как параметр анимации. Колесо понято как круг. Существует 3 точки, зафиксированные к колесу: зеленая точка на оправе, красная точка в колесе и синяя точка вне колеса:
WheelRadius := 1:
WheelCenter := [x, WheelRadius]:
WheelRim := plot::Circle2d(WheelRadius, WheelCenter,
x = 0..4*PI,
LineColor = RGB::Black):
WheelHub := plot::Point2d(WheelCenter, x = 0..4*PI,
PointColor = RGB::Black):
WheelSpoke := plot::Line2d(WheelCenter,
[WheelCenter[1] + 1.5*WheelRadius*sin(x),
WheelCenter[2] + 1.5*WheelRadius*cos(x)],
x = 0..4*PI, LineColor = RGB::Black):
color:= [RGB::Red, RGB::Green, RGB::Blue]:
r := [1.5*WheelRadius, 1.0*WheelRadius, 0.5*WheelRadius]:
for i from 1 to 3 do
Point[i] := plot::Point2d([WheelCenter[1] + r[i]*sin(x),
WheelCenter[2] + r[i]*cos(x)],
x = 0..4*PI,
PointColor = color[i],
PointSize = 2.0*unit::mm):
Cycloid[i] := plot::Curve2d([y + r[i]*sin(y),
WheelRadius + r[i]*cos(y)],
y = 0..x, x = 0..4*PI,
LineColor = color[i]):
end_for:
plot(WheelRim, WheelHub, WheelSpoke,
Point[i] $ i = 1..3,
Cycloid[i] $ i = 1..3,
Scaling = Constrained,
Width = 120*unit::mm, Height = 60*unit::mm):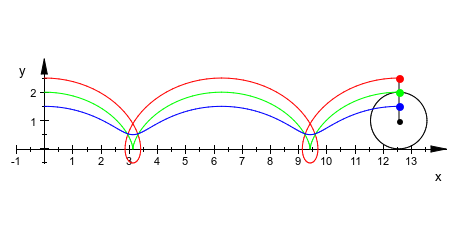
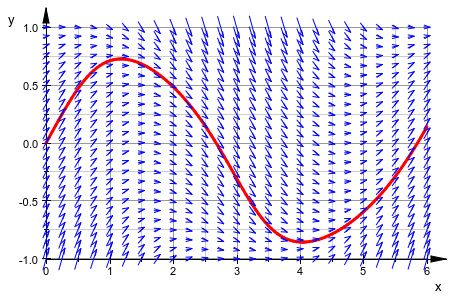
Мы хотим визуализировать решение обыкновенного дифференциального уравнения (ODE)![]() с начальным условием y (0) = 0. Решение должно чертиться вместе с векторным полем
с начальным условием y (0) = 0. Решение должно чертиться вместе с векторным полем![]() , сопоставленным с этим ОДУ (вдоль кривой решения, векторы этого поля являются касательными кривой). Мы используем
, сопоставленным с этим ОДУ (вдоль кривой решения, векторы этого поля являются касательными кривой). Мы используем numeric::odesolve2, чтобы сгенерировать решение как график функций. Поскольку числовой интегратор возвращает результат как список одного значения с плавающей точкой, нужно передать одну запись списка как Y(x)[1] к plot::Function2d. Векторное поле сгенерировано через plot::VectorField2d:
f := (x, y) -> -y^3 + cos(x):
Y := numeric::odesolve2(
numeric::ode2vectorfield({y'(x) = f(x, y), y(0) = 0},
[y(x)])):
plot(
plot::Function2d(Y(x)[1], x = 0..6, Color = RGB::Red,
LineWidth = 0.7*unit::mm),
plot::VectorField2d([1, f(x, y)], x = 0..6, y = -1..1,
Color = RGB::Blue, Mesh = [25, 25]),
GridVisible = TRUE, SubgridVisible = TRUE, Axes = Frame
):
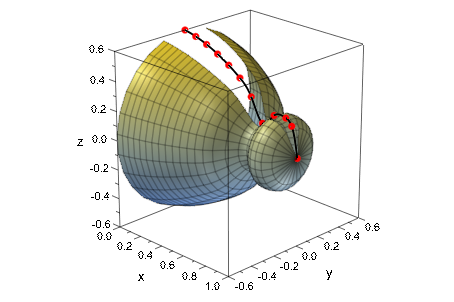
Радиус r объекта с осевой симметрией вокруг x - ось измеряется в различных положениях x:
| x | 0.00 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 | 0.90 | 0.95 | 1.00 |
| r (x) | 0.60 | 0.58 | 0.55 | 0.51 | 0.46 | 0.40 | 0.30 | 0.15 | 0.23 | 0.24 | 0.20 | 0.00 |
Интерполяция сплайна используется, чтобы задать сглаженный функциональный r (x) от измерений:
samplepoints :=
[0.00, 0.60], [0.10, 0.58], [0.20, 0.55], [0.30, 0.51],
[0.40, 0.46], [0.50, 0.40], [0.60, 0.30], [0.70, 0.15],
[0.80, 0.23], [0.90, 0.24], [0.95, 0.20], [1.00, 0.00]:
r := numeric::cubicSpline(samplepoints):Мы восстанавливаем объект как поверхность вращения через plot::XRotate. Угол поворота ограничивается областью значений, которая оставляет разрыв на поверхности. Сплайновая кривая и точки выборки добавлены как plot::Curve3d и plot::PointList3d, соответственно, и отображены в этом разрыве:
plot(
plot::XRotate(r(x), x = 0..1, AngleRange = 0.6*PI..2.4*PI,
Color = RGB::MuPADGold),
plot::Curve3d([x, 0, r(x)], x = 0..1,
LineWidth = 0.5*unit::mm, Color = RGB::Black),
plot::PointList3d([[p[1], 0, p[2]] $ p in samplepoints],
PointSize = 2.0*unit::mm,
Color = RGB::Red),
CameraDirection = [70, -70, 40]
):
Следующая сумма является представлением Фурье периодической ступенчатой функции:
![]()
Мы хотим показать сходимость частичных сумм
![]()
для некоторых маленьких значений n. С этой целью мы присваиваем значение f n (x) к MuPAD identifier f_n. Для нашего второго и третьего примера мы должны будем принять дробные значения n, таким образом, код будет использовать floor, чтобы получить “соответствующее” целочисленное значение для суммы:
f_n := sum(sin((2*k-1)*x)/(2*k-1), k = 1..floor(n))
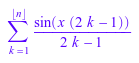
Во-первых, мы используем plotfunc2d и оператор последовательности $, чтобы построить первые 5 частичных сумм в ту же систему координат (и выключать легенду, которая не полезна для этого приложения).
plotfunc2d(f_n $ n = 1..5, LegendVisible = FALSE)
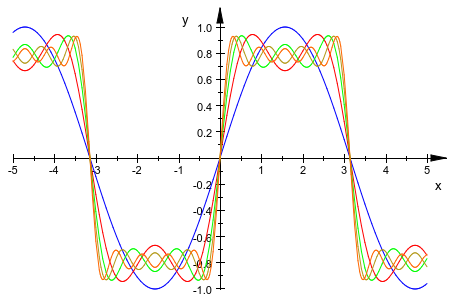
Этот график ясно показывает то, что известно как явление Гиббса: В разрывах ступенчатой функции, приближение “перерегулирования”. Графический вывод большего количества приближений одновременно собирается создать слишком переполненный график быть полезным, так чтобы показать, что использование большего количества терминов в сумме не помогает против явления Гиббса, мы возвращаемся к анимациям, чтобы показать первые 30 частичных сумм – это - одна из причин, мы использовали floor(n) выше:
plotfunc2d(f_n, x = -5..5, n = 1..30, Frames = 15)
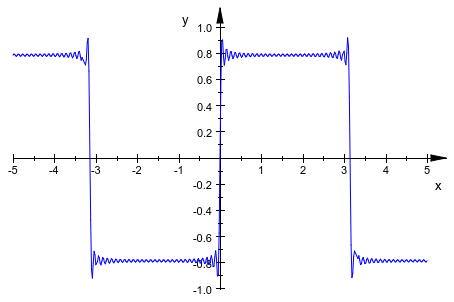
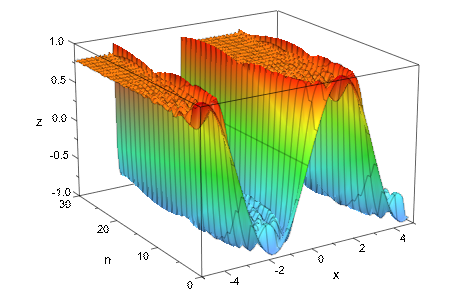
Другая возможность показа поведения сходимости состоит в том, чтобы создать 3D график со второй ординатой, являющейся количеством терминов, использованных в приближении:
plotfunc3d(f_n, x = -5..5, n = 1..30,
Submesh = [5,1], FillColorType = Rainbow)