Exponenta Banner

Dom::LinearOrdinaryDifferentialOperator

Область линейных операторов полного дифференциала

расширьте все на странице

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

Доменное создание

Dom::LinearOrdinaryDifferentialOperator(<Var, <DVar, <Ring>>>)

Создание элемента

Dom::LinearOrdinaryDifferentialOperator(Var, DVar, Ring)(p)
Dom::LinearOrdinaryDifferentialOperator(Var, DVar, Ring)(l)
Dom::LinearOrdinaryDifferentialOperator(Var, DVar, Ring)(eq, yx)

Описание

Dom::LinearOrdinaryDifferentialOperator(Var, DVar, Ring) создает область линейных операторов полного дифференциала с коэффициентами в дифференциальном кольцевом Ring и с деривацией Var где DVar неопределенный дифференциал. Элементы этой области также называются полиномами Руды, и умножение двух элементов полностью определяется предписанным правилом для каждого элемента r в Ring. И так Dom::LinearOrdinaryDifferentialOperator некоммутативный звонок.

Примечание

Тем не менее, по некоторым причинам, по каждому элементу r в Ring, Var*r автоматически переписан как r*Var. Смотрите пример 1.

Если Dom::LinearOrdinaryDifferentialOperator называется без любого аргумента, области с коэффициентами в Dom::ExpressionField(normal) с деривацией Df и дифференциальный неопределенный x создается.

Примечание

Только коммутативные дифференциальные звонки типа DOM_DOMAIN позволены, которые наследовались Dom::BaseDomain. Если Ring имеет тип DOM_DOMAIN но не наследовался Dom::BaseDomain, доменный Dom::ExpressionField(normal) будет использоваться вместо этого.

Примечание

Это, настоятельно рекомендуют использовать только содействующие звонки с уникальным нулевым представлением. В противном случае это может произойти, который, например, не отключит полиномиальное деление, или будет возвращена неправильная степень.

Примеры

Пример 1

Сначала мы создаем область линейных операторов полного дифференциала:

lodo := Dom::LinearOrdinaryDifferentialOperator()

значением по умолчанию вышеупомянутая область имеет коэффициенты в поле Dom::ExpressionField(normal) с деривацией Df и дифференциальный неопределенный x.

Мы можем создать элементы lodo 3 способами: полиномы в Df, список элементов Dom::ExpressionField и с линейным обычным гомогенным дифференциальным уравнением:

lodo(Df^2 + (x + 1)*Df + 2*x), lodo([2*x, x + 1, 1]),
lodo(diff(y(x),x,x) + (x + 1)*diff(y(x),x) + 2*x*y(x), y(x))

Легко получить линейное дифференциальное уравнение, сопоставленное к линейному дифференциальному оператору:

L := lodo((x + x^3)*Df^3 + (6*x^2 + 3)*Df^2 - 12):
L(y(x))

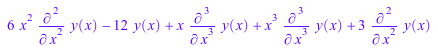
и каждый может также оценивать дифференциальный оператор при выражении:

L(2*x^2 + 1), L(ln(x)), L(ln(x), Unsimplified)

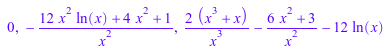
Умножение элементов lodo является некоммутативным, но для каждого элемента r из содействующего звонка у каждого есть Df*r = r*Df:

lodo(x^2*Df), lodo(Df*x^2), lodo(Df)*lodo(x^2)

Пример 2

Dom::LinearOrdinaryDifferentialOperator область, где Евклидово деление существует, но каждый имеет к точному, если умножение 2 элементов этой области сделано справа или на левой стороне:

L1 := lodo(x*Df^3 + (x^2 - 3)*Df^2 + 4*x*Df + 2):
lodo::leftDivide(L1,lodo(x*Df + 1))

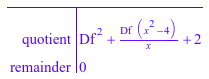
lodo(x*Df + 1) * %[quotient] = L1

Следовательно у каждого есть понятия наибольшего общего делителя, наименьшее общее кратное справа и слева, и модифицированная версия расширенного Алгоритма Евклида:

L2 := lodo(x*Df + 1):
ree := lodo::rightExtendedEuclid(L1,L2)

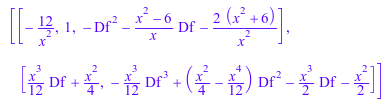
Правильный наибольший общий делитель и левое наименьшее общее кратное могут быть считаны из вышеупомянутого списка:

iszero(lodo::rightGcd(L1,L2) - ree[1][1]), 
iszero(ree[1][1] - (ree[1][2]*L1 + ree[1][3]*L2)),
iszero(lodo::leftLcm(L1,L2) - (-ree[2][1]*L1)), 
iszero(-ree[2][1]*L1 - ree[2][2]*L2)

Пример 3

Можно вычислить полином, рациональные и экспоненциальные нули линейных дифференциальных операторов любой степени обеспечили кольцевой Ring поле рациональных функций x

L3 := lodo((x^2 + 1)*x*Df^3 + 3*(2*x^2 + 1)*Df^2 - 12):
lodo::rationalZeros(L3), lodo::exponentialZeros(L3)

даже когда оператор содержит некоторые параметры рационально:

lodo::exponentialZeros(
lodo(Df^4 + (b*l - 2*a^2 - a*l*x)*Df^2 + a^4-a^2*b*l + a^3*l*x))

Пример 4

Можно разложить на множители линейные дифференциальные операторы в неприводимые факторы когда кольцевой Ring поле рациональных функций x. Тем не менее, алгоритм завершен только для операторов степени самое большее 3; для более высокой степени только найдены левые и правые факторы степени 1:

factor(lodo((x^2 + 1)*x*Df^3 + 3*(2*x^2 + 1)*Df^2 - 12)),
factor(lodo(Df^3 + a*x*Df + a + b^3 + a*b*x))

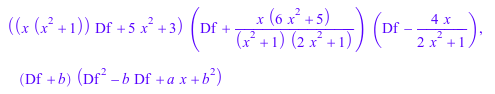
Здесь факторы оператора в два фактора степени 2, который не может быть найден MuPAD®:

factor(lodo(Df^2 + x^3 + 1/x^3) * lodo(Df^2 + x^2 - 1/x^3))

Пример 5

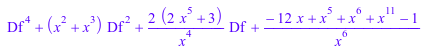
Решение линейных дифференциальных операторов с помощью команды solve также возможно:

solve(lodo(Df^2 + (3 - x)/(16*x^2)))

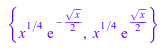
Для определенных случаев, где группы сопоставили к dfferential операторам, конечные примитивные группы степени 2, полином возвращен, соответствуя минимальному полиному всех нулей дифференциального оператора (они являются алгебраическими по основному полю):

solve(lodo(Df^2 + 
      (-27*x + 32*x^2 + 27)/(144*x^2 - 288*x^3 + 144*x^4)))

Поскольку линейные дифференциальные операторы степени, больше, чем 3 только экспоненциальных нуля, будут найдены:

solve(lodo(x*Df^4 + (-x + 4)*Df^3 - 3*Df^2 - x^2*Df - x + x^2))

Определенная вторая степень линейный дифференциальный оператор может быть решена в терминах некоторых специальных функций (nonliouvillian функции), такие как airyAibesseli и whittakerM:

solve(lodo(Df^2 - (x + 1)/(x - 1)^5))

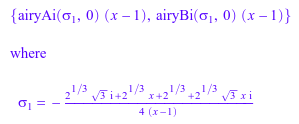
solve(lodo(Df^2 - (243 + 4*x^8 + 162*x^2 + 19*x^4)/
                   36/x^2/(x^2 + 3)^2))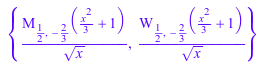

Параметры

Var

Неопределенный из типа DOM_IDENT. Значением по умолчанию является Df.

DVar

Дифференциал, неопределенный из типа DOM_IDENT. Значением по умолчанию является x.

Ring

Произвольный коммутативный дифференциальный звонок характеристического нуля. Значением по умолчанию является Dom::ExpressionField(normal).

p

Многочленное выражение в Var.

l

Список, соответствующий коэффициентам дифференциального оператора. Если n является длиной l затем возвращенным результатом является l[1] + l[2]*Var + ... + l[n]*Var^(n-1).

eq

Линейное гомогенное дифференциальное уравнение.

yx

Функция DVar представление зависимой переменной вышеупомянутого линейного дифференциального уравнения.

Методы

развернуть все

Математические методы

_mult(<a, b, …>)

Этот метод перегружает функциональный _mult из системного ядра, т.е. можно использовать его любой в форме a * b * ... или в функциональном обозначении _mult(a, b, ...).

_negate(a)

Этот метод перегружает функциональный _negate из системного ядра, т.е. можно использовать его любой в форме -a или в функциональном обозначении _negate(a).

_plus(<a, b, …>)

Этот метод перегружает функциональный _plus из системного ядра, т.е. можно использовать его любой в форме a + b + ... или в функциональном обозначении _plus(a, b, ...).

_power(a, n)

Этот метод перегружает функциональный _power из системного ядра, т.е. можно использовать его любой в форме a^n или в функциональном обозначении _power(a,n).

_subtract(a, b)

Этот метод перегружает функциональный _subtract из системного ядра, т.е. можно использовать его любой в форме a - b или в функциональном обозначении _subtract(a, b).

adjoint(a)

companionSystem(a)

Если a не имеет положительной степени, сообщение об ошибке выпущено.

D(<l>, a)

Dpoly(<l>, a)

Dpoly(l,a) вычисляет частную производную a относительно l. Если l = [1,...,1] с length(l) = n затем метод вычисляет n- производная th a. Если l = [] затем возвращенным результатом является a.

evalLODO(a, f)

Этот метод может использоваться любой в форме a(f) или в функциональном обозначении evalLODO(a,f).

exponentialZeros(a)

Примечание

Этот метод только работает когда Ring поле рациональных функций в DVar.

factor(a)

Примечание

Этот метод только доступен когда основное поле Ring поле рациональных функций в DVar. Если a имеет степень, больше, чем или равен 4 затем только левые и правые факторы степени 1 из a будет найден. В противном случае полная факторизация возвращена.

Этот метод перегружает функциональный factor из системного ядра.

factors(a)

func_call(a, f, <Unsimplified>)

Этот метод может использоваться любой в форме a(f) или в функциональном обозначении func_call(a,f).

leftDivide(a, b)

leftExtendedEuclid(a, b)

leftExtendedGcd(a, b)

leftGcd(a, b)

leftLcm(a, b)

leftQuotient(a, b)

leftRemainder(a, b)

makeIntegral(a)

monic(a)

polynomialZeros(a)

Примечание

Этот метод только работает когда Ring поле рациональных функций в DVar.

rationalZeros(a)

Примечание

Этот метод только работает когда Ring поле рациональных функций в DVar.

rightDivide(a, b)

rightExtendedEuclid(a, b)

rightExtendedGcd(a, b)

rightGcd(a, b)

rightLcm(a, b)

rightQuotient(a, b)

rightRemainder(a, b)

solve(a, <Transform>, <Irreducible>)

Алгоритм для нахождения liouvillian решения завершен для операторов степени самое большее 2 и включает, чтобы решить частично операторы более высокой степени (т.е. это находит все экспоненциальные решения). Алгоритм для нахождения решений в терминах специальных функций (nonliouvillian решения) не завершен даже для степени 2.

Когда опция Transform дан unimodular преобразование выполняется безусловно и когда опция Irreducible дан, a принят, чтобы быть неприводимым.

Примечание

Этот метод только работает когда Ring поле рациональных функций в DVar.

Этот метод перегружает функциональный solve из системного ядра.

symmetricPower(a, m)

unimodular(a, <Transform>)

Если опция Transform дан затем a преобразовывается безусловно даже если a имеет все же unimodular группу Галуа.

Методы доступа

coeff(a)

coeff(a, Var, n)

coeff(a, n)

coeff(a,Var,n) возвращает коэффициент термина Var^n как элемент коэффициента звонят Ring, где a линейный дифференциальный оператор в переменной Var.

coeff(a,n) возвращает коэффициент термина Var^n как элемент коэффициента звонят Ring, где a линейный дифференциальный оператор в переменной Var.

Этот метод перегружает функциональный coeff из системного ядра.

degree(a)

Степень нулевого полинома задана как нуль.

Этот метод перегружает функциональный degree для полиномов.

vectorize(a)

Методы преобразования

convert(a)

FAIL возвращен, если преобразование перестало работать.

expr(a)

Этот метод перегружает функциональный expr из системного ядра.

Алгоритмы

Некоторые ссылки на линейных дифференциальных уравнениях/операторах:

Смотрите также

Области MuPAD

Документация Symbolic Math Toolbox
Поддержка