plot::RootlocusКривые корней рациональных выражений
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
plot::Rootlocus(p(z, u), u = umin .. umax, <a = amin .. amax>, options)
plot::Rootlocus(p(z, u), u = umin.. umax) создает 2D график кривых в комплексной плоскости, данной полностью p (z, u) = 0 (решенный для z) как параметр, u варьируется между umin и umax.
Для любого данного значения u, plot::Rootlocus решает уравнение p (z, u) = 0 для z. Решения задают точки с координатами x = ℜ (z), y = ℑ (z) в комплексной плоскости. Как параметр варьируется u, решения формируют непрерывные кривые что изображенный plot::Rootlocus.
Корни числителя p(z, u) рассматриваются. Все сложные решения этого полинома в z вычисляются численно через numeric::polyroots.
Полином первоначально решен для некоторых значений u из области значений u = `u_{min}` .. `u_{max}`. Дополнительный аргумент Mesh = n может использоваться, чтобы задать номер n этих начальных точек (значение по умолчанию равняется 51). Эти точки не равномерно распределены, но накапливаются близко к концу области значений.
Стандартная программа затем пытается разделить на пары корни для смежных значений u путем выбора самых близких друг к другу.
Наконец, стандартная программа пытается проследить различные кривые путем соединения смежных точек с линейными сегментами. Если сегменты смежной строки показывают углы, которые не являются близко к 180 градусам, дополнительные корни вычисляются для значений параметров u между значениями начальной mesh. До m такие шаги bisectioning возможны, где m задан дополнительным аргументом AdaptiveMesh = m (значение по умолчанию равняется 4). С AdaptiveMesh = 0, этот адаптивный механизм может быть выключен.
Иногда, совпадение корней к непрерывным кривым можно дурачить, и результатом является грязный график. В таком случае пользователь может принять следующие меры, чтобы улучшить график:
Область значений параметра u = `u_{min}` .. `u_{max}` может быть необоснованно большим. Уменьшайте эту область значений до разумного размера!
Увеличьте размер n начальной mesh с помощью опции Mesh = n. Обратите внимание на то, что увеличение n некоторым фактором может увеличить время выполнения графика того же фактора!
Увеличьте число m возможных адаптивных шагов bisectioning с помощью опции AdaptiveMesh = m. Обратите внимание на то, что увеличение m 1 может увеличить время выполнения графика фактора 2!
Используя опции LinesVisible = FALSE в сочетании с PointsVisible = TRUE, корни отображены как отдельные точки, не соединяя линейные сегменты.
См. пример 2.
Анимации инициированы путем указания диапазона a = `a_{min}` .. `a_{max}` для параметра a это отличается от переменных z и u. См. пример 3.
Кривые могут быть окрашены схемой определяемого пользователем цвета. Только передайте опцию LineColorFunction = mycolor, где mycolor пользователь definied процедура, которая возвращает RGB значение цвета. Стандартный plot::Rootlocus вызовы mycolor(u, x, y), где u является значением параметров и x, y действительные и мнимые части корня p (x + i y, u) = 0. См. Пример 4.
| Атрибут | Цель | Значение по умолчанию |
|---|---|---|
AdaptiveMesh | адаптивная выборка | 4 |
AffectViewingBox | влияние объектов на ViewingBox из сцены | TRUE |
AntiAliased | сглаженные линии и точки? | TRUE |
Frames | количество систем координат в анимации | 50 |
Legend | делает запись легенды | |
LegendText | короткий объяснительный текст для легенды | |
LegendEntry | добавить этот объект в легенду? | FALSE |
LineColor | цвет линий | RGB::Blue |
LineWidth | ширина линий | 0.35 |
LineStyle | тело, подчеркнутые штриховой линией или пунктирные линии? | Solid |
LinesVisible | видимость линий | TRUE |
LineColorType | типы окраски линии | Flat |
LineColorFunction | функциональная окраска линии | |
Mesh | количество точек выборки | 51 |
Name | имя объекта графика (для браузера и легенды) | |
ParameterEnd | закончите значение параметра анимации | |
ParameterName | имя параметра анимации | |
ParameterBegin | начальное значение параметра анимации | |
ParameterRange | область значений параметра анимации | |
PointSize | размер точек | 1.0 |
PointStyle | стиль презентации точек | FilledCircles |
PointsVisible | видимость точек mesh | FALSE |
RationalExpression | рациональное выражение в графике rootlocus | |
TimeEnd | время окончания анимации | 10.0 |
TimeBegin | время начала анимации | 0.0 |
TimeRange | оперативный промежуток анимации | 0.0 |
Title | объектный заголовок | |
TitleFont | шрифт объектных заголовков | [" sans-serif ", 11 |
TitlePosition | положение объектных заголовков | |
TitleAlignment | выравнивание по горизонтали заголовков w.r.t. их координаты | Center |
TitlePositionX | положение объектных заголовков, x компонент | |
TitlePositionY | положение объектных заголовков, y компонент | |
UMax | окончательное значение параметра “u” | |
UMesh | количество точек выборки для параметра “u” | 51 |
UMin | начальное значение параметра “u” | |
UName | имя параметра “u” | |
URange | область значений параметра “u” | |
Visible | видимость | TRUE |
VisibleAfter | объект, видимый после этой временной стоимости | |
VisibleBefore | объект, видимый до этой временной стоимости | |
VisibleFromTo | объект, видимый в это время, располагается | |
VisibleAfterEnd | объект, видимый после его законченного времени анимации? | TRUE |
VisibleBeforeBegin | объект, видимый перед его временем анимации, запускается? | TRUE |
Корнями полиномиального z 2 - 2 u z + 1 дают![]() и
и![]() . Мы визуализируем эти две кривые с помощью графика rootlocus:
. Мы визуализируем эти две кривые с помощью графика rootlocus:
plot(plot::Rootlocus(z^2 - 2*u*z + 1, u = -1.5..1.5))
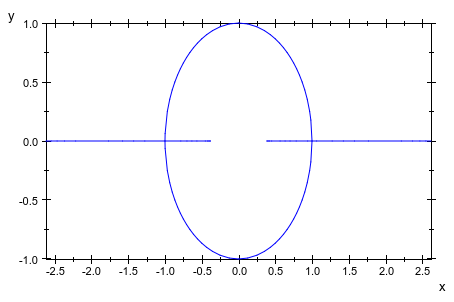
Для рациональных выражений рассматриваются корни числителя. Следующий график отображает корни полинома числителя (z 2 - u) 2 + u (z - u) 3:
plot(plot::Rootlocus(1 + u * (z - u)^3/(z^2 - u)^2, u = -1..1)):
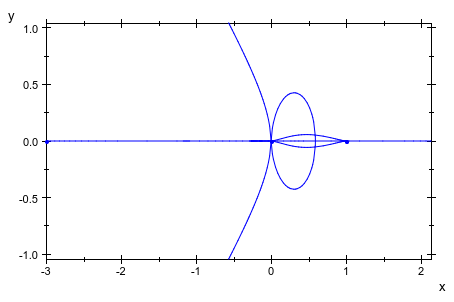
Вот различные другие примеры:
plot(plot::Rootlocus((z^2 - 2*u*z + 1)^2 + u, u = -1..1))
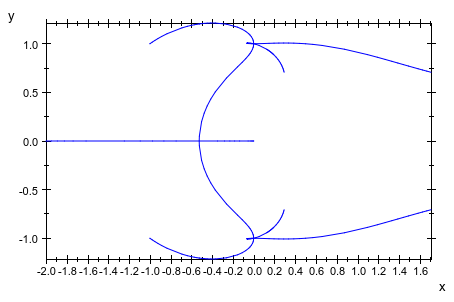
plot(plot::Rootlocus((z^2 - u)^6 + u^2, u = -2..2,
Color = RGB::Red))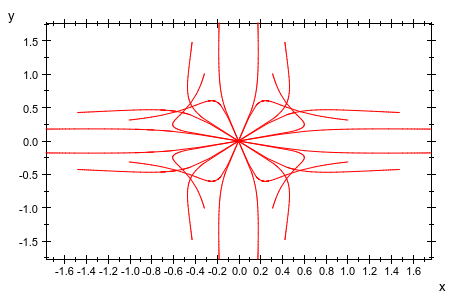
plot(plot::Rootlocus((z^5 - 1)^3 + u, u = -1..1, PointsVisible,
PointSize = 1.5))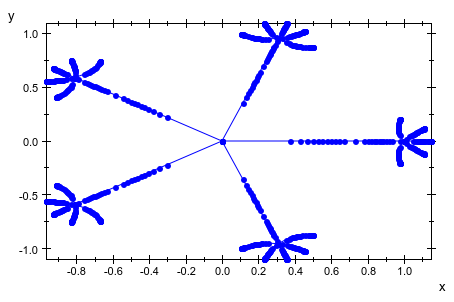
Следующий график довольно грязен, поскольку размер mesh по умолчанию 51 начальной точки на каждой кривой не достаточен, чтобы получить хорошее разрешение:
plot(plot::Rootlocus((z-u)^3 - u/z^3, u = -10^3 .. 10^3)):
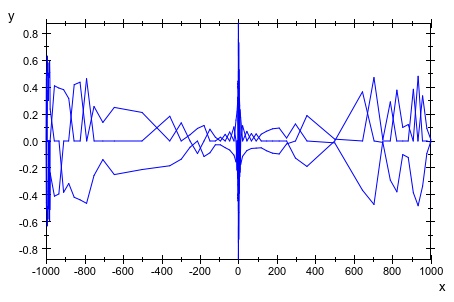
Мы получаем лучшее разрешение путем уменьшения области значений параметра u к разумному размеру. Существует все еще несколько точек, которые правильно не подходятся в кривых:
plot(plot::Rootlocus((z-u)^3 - u/z^3, u = -10 .. 10)):
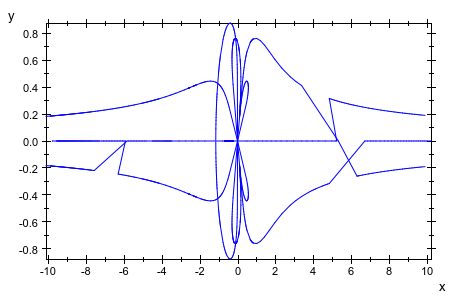
Мы увеличиваем размер mesh, чтобы исправить эту проблему:
plot(plot::Rootlocus((z-u)^3 - u/z^3, u = -10 .. 10, Mesh = 251)):
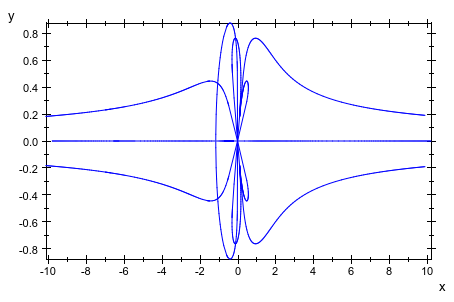
Мы строим корни как отдельные точки, не отображая сегменты соединительной линии:
plot(plot::Rootlocus((z-u)^3 - u/z^3, u = -10 .. 10, Mesh = 501,
LinesVisible = FALSE, PointsVisible)):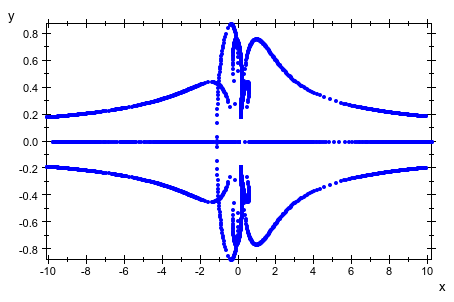
Мы анимируем выражение, корни которого к нанесенному на график:
plot(plot::Rootlocus(z^2 - 2*u*z + a, u = -1..1, a = -0.2 .. 2, Mesh = 10),
plot::Text2d(a -> "a = ".stringlib::formatf(a, 2, 5), [1.2, 1.0], a = -0.2 .. 1));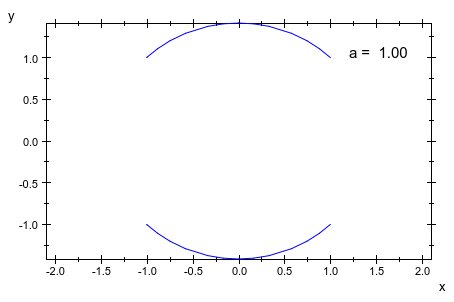
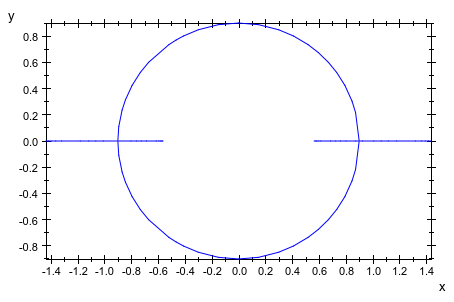
Мы анимируем область значений параметра:
plot(plot::Rootlocus(z^2 - 2*u*z + 0.81, u = -1 .. a, a = -1 .. 1, Mesh = 10))
Мы обеспечиваем функцию управления цветом: поддерживает маленькие значения параметра, u отображен в красном, тогда как поддерживает большие значения параметров, отображены в синем:
plot(plot::Rootlocus(z^2 - 2*u*z + 0.81, u = -1..1,
LineColorFunction = ((u, x, y) -> [(1 - u)/2, 0, (1 + u)/2])))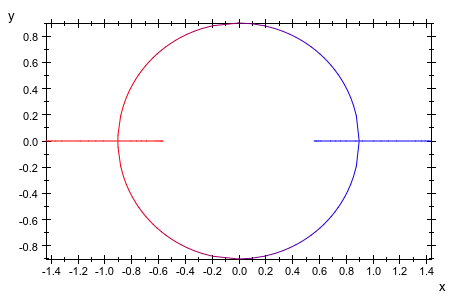
|
Арифметическое выражение в двух неизвестных z и u и, возможно, параметр анимации
|
|
Имя неизвестного: идентификатор или индексируемый идентификатор. |
|
Имя параметра кривой: идентификатор или индексируемый идентификатор.
|
|
Область значений параметра кривой: |
|
Параметр анимации, заданный как |