AdaptiveMeshАдаптивная выборка
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
| Наследованный | Неотрицательное целое число |
| Объекты | Значения по умолчанию AdaptiveMesh |
|---|---|
plot::Function2d | 2 |
plot::Conformal, plot::Curve2d, plot::Curve3d, plot::Cylindrical, plot::Function3d, plot::Implicit3d, plot::Polar, plot::SphericalПоверхность графика, plot::Sweep, plot::XRotate, plot::ZRotate | 0 |
plot::Rootlocus | 4 |
AdaptiveMesh = n управляет адаптивной выборкой в численной оценке функций, кривых и поверхностей. С n = 0, отключена адаптивная выборка. С n> 0, включена адаптивная выборка.
“Глубина” n адаптивной выборки должна быть маленьким целым числом такой как 0, 1, 2, или 3.
Непрерывные графические объекты, такие как функциональные графики, параметризованные кривые и поверхности аппроксимированы дискретной сеткой числовых точек.
Этой mesh может управлять пользователь через атрибуты Mesh, Submesh, и AdaptiveMesh. (В зависимости от объекта, Mesh припишите разделения в более определенные версии такой нас UMesh и VMesh для кривой и объемных поверхностных диаграмм или XMesh, YMesh, ZMesh для функции и неявных графиков.)
Во-первых, объект оценен численно на равноотстоящей “начальной mesh” набор через атрибут Mesh (или более определенные упомянутые выше версии).
С AdaptiveMesh = 0, числовые данные по начальной mesh используются, чтобы представить объект без дальнейшего адаптивного улучшения.
С AdaptiveMesh = n, n> 0, далее числовые данные вычисляются, прежде чем средство отображения называется. В частности, данные соседних точек на начальной mesh исследованы. Если точка обоснованно не представлена прямой линией, соединяющей соседние точки, соответствующие интервалы начальной mesh подразделены рекурсивно. Адаптивный механизм убывает на подынтервалы начальной mesh, если последовательные линейные сегменты дискретизированного объекта графика отклоняются от прямой линии “углом поворота” больше чем 10 градусов. Интервалы, вовлеченные в такую ситуацию, разделены в половины, рекурсивно.
Значение n должно быть маленьким целым числом, которое определяет рекурсивную глубину адаптивного улучшения. В каждом направлении до 2n - 1 дополнительная точка помещается между точками начальной mesh.
Если объект выглядит гладко на начальном наборе mesh через атрибут Mesh или его более подробные варианты, адаптивный механизм не убывает на интервалы начальной mesh. Если существуют микроструктуры, скрытые в этих интервалах, задавая AdaptiveMesh = n с n> 0 не поможет улучшить график. В таком случае начальная mesh должна быть усовершенствована через соответствующий атрибут для начальной mesh.
С другой стороны, если начальная mesh достаточно прекрасна, чтобы указать на более прекрасные внутренние структуры через “макс. угловой критерий” поворота, часто более эффективно использовать AdaptiveMesh = n чем совершенствовать начальную mesh, потому что адаптивный механизм совершенствовал только те части объекта, которым действительно нужно улучшение. Этот эффект виден в Примере 3.
Обратите внимание на то, что увеличивая рекурсивную глубину n на 1 может увеличить время выполнения на фактор 2 для объектов линии (2D функциональные графики и кривые) и фактором 4 для объектов подложки (3D функциональные графики и поверхности). В большинстве случаев маленькое значение, такое как n ∈ {1, 2, 3} достаточно, чтобы получить довольно сглаженный объект графика.
Обратите внимание на то, что адаптивный алгоритм для объектов подложки в 3D является очень дорогим! Как альтернатива значениям n> 0 в AdaptiveMesh = n, можно экспериментировать с AdaptiveMesh = 0, Submesh = [2n- 1, 2n- 1] в 3D функциональных графиках или поверхностях. Гранулярность “начальной mesh”, сгенерированной с этими значениями атрибута, приблизительно одного размера с адаптивной mesh, сгенерированной с AdaptiveMesh = n, Submesh = [0, 0]. Неадаптивная оценка на усовершенствованной регулярной mesh может все еще быть более эффективной, чем оценка на (неправильной) неадаптивной mesh.
Следующий график функций содержит области высокого изменения. Без спецификации AdaptiveMesh, режим по умолчанию AdaptiveMesh = 0 используется и мы ясно видим артефакты, вызванные оценкой на дискретной mesh:
plot(plot::Function2d(
sin(x) + exp(-5*(x - PI/2)^2)*sin(110*x)/10, x = 0..PI)):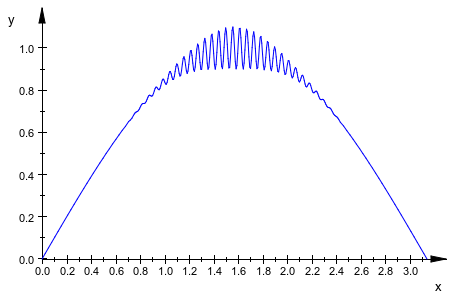
Мы активируем адаптивное улучшение высоким уровнем 3:
plot(plot::Function2d(
sin(x) + exp(-5*(x - PI/2)^2)*sin(110*x)/10, x = 0..PI,
AdaptiveMesh = 3)):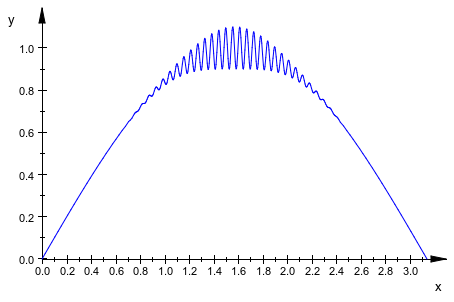
Мы устанавливаем атрибут PointsVisible = TRUE так, чтобы точки адаптивной mesh стали видимыми:
plot(plot::Function2d(
sin(x) + exp(-5*(x - PI/2)^2)*sin(110*x)/10, x = 0..PI,
AdaptiveMesh = 3, PointsVisible = TRUE)):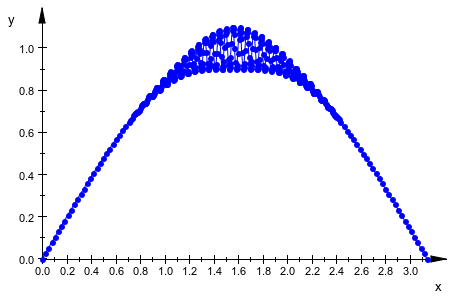
Значение по умолчанию Mesh не обеспечивает достаточное разрешение для следующей спирали:
plot(plot::Curve2d([x*cos(x), x*sin(x)], x = 0..50*PI)):
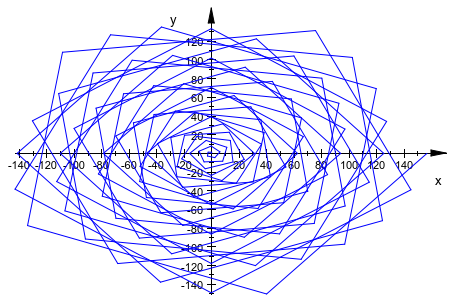
Увеличение Mesh значение улучшает график:
plot(plot::Curve2d([x*cos(x), x*sin(x)], x = 0..50*PI,
Mesh = 1000)):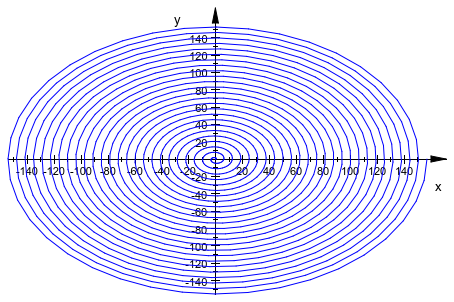
В качестве альтернативы адаптивный графический вывод может использоваться:
plot(plot::Curve2d([x*cos(x), x*sin(x)], x = 0..50*PI,
AdaptiveMesh = 3)):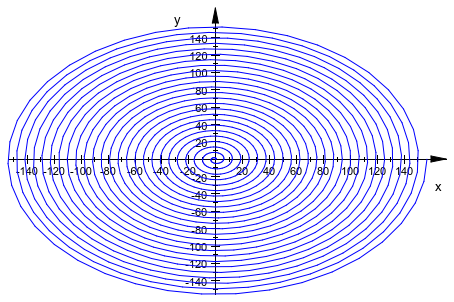
В 3D типичные артефакты, вызванные прямолинейной начальной mesh, являются “вмятинами” на поверхностных функциях, которые не параллельны оси параметра. Без спецификации AdaptiveMesh, режим по умолчанию AdaptiveMesh = 0 используется:
f := plot::Function3d(sin(x*y)/(abs(x*y) + 1),
x = -4 .. 4, y = -4 .. 4):
plot(f):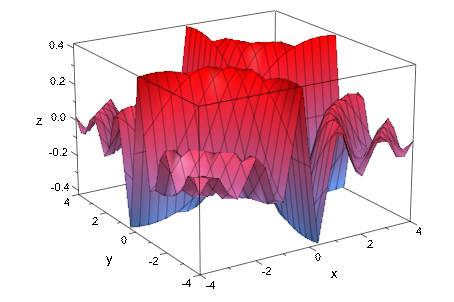
Активируя адаптивное улучшение, мы получаем намного более точный график. Однако расчет берет намного дольше:
plot(f, AdaptiveMesh = 2):
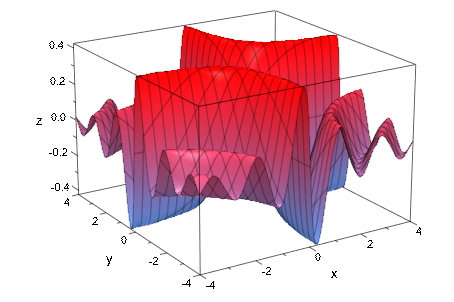
Насколько локальный улучшение, мы устанавливаем атрибут MeshVisible = TRUE так, чтобы внутренняя триангуляция адаптивной mesh стала видимой:
plot(f, AdaptiveMesh = 2, MeshVisible = TRUE):
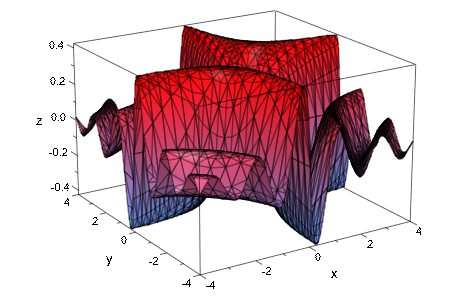
Мы используем неадаптивную оценку, но совершенствовали регулярную mesh установкой Submesh значения 2n - 1, которые соответствуют адаптивной глубине n = 2 используемых выше. Результат имеет подобное качество как прежде:
plot(plot::Function3d(sin(x*y)/(abs(x*y) + 1),
x = -4 .. 4, y = -4 .. 4,
Submesh = [3, 3])):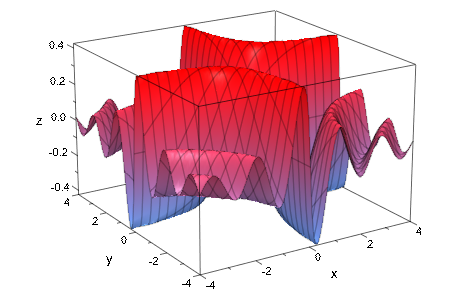
delete f: