При моделировании динамической системы, которая не начинается с отдыха, необходимо инициализировать моделирование в соответствии с начальными условиями. Например, можно сравнить смоделированный отклик с измеренными данными или с предыдущим моделированием или вычислением. Можно начать моделирование в установившемся состоянии или продолжить моделирование из предыдущего моделирования.
Toolbox™ идентификации системы предоставляет множество методов определения исходных условий (ИС) для использования. Эти методы включают использование:
Результаты идентификации модели
Текущие или прошлые измерения входных/выходных данных
Сведения о состоянии из предыдущего моделирования
В следующей таблице представлены доступные подходы и способы их использования. Для краткости эта таблица использует термин «моделирование» в широком смысле для обозначения «моделирование или прогнозирование». Дополнительные сведения см. в разделе Моделирование и прогнозирование вывода идентифицированной модели.
Подходы к оценке начальных условий
| Когда использовать | Подход | Сводка по методу |
|---|---|---|
Вы имитируете idss,idtf, idproc, idpoly, или idgrey отклик модели с использованием тех же входных данных, с которыми была идентифицирована модель. | Извлеките ИС из результатов идентификации модели (возвращенные значения или отчет об оценке). Оценка возвращает информацию ИС в одной из следующих форм.
См. раздел Оценка начальных условий на основе измеренных данных. |
Примеры: Разрешение расхождений значений подгонки между идентификацией модели и командой сравнения Применение начальных условий при моделировании идентифицированных линейных моделей |
Вы хотите воспроизвести результаты, созданные compare (или генерируется графиком «Вывод модели» в приложении). | Использовать возвращенные IC из См. раздел Оценка начальных условий на основе измеренных данных. |
Примеры: Совпадение выходных данных команды сравнения и нелинейного блока модели ARX Применение начальных условий при моделировании идентифицированных линейных моделей |
| Вы имитируете отклик модели на заданный входной сигнал и хотите начать моделирование в точке, которая приводит к ближайшему совпадению с заданным выходным сигналом. | Использовать Использовать Если исходная модель См. раздел Оценка начальных условий на основе измеренных данных. |
Примеры: Применение начальных условий при моделировании идентифицированных линейных моделей Оценка начальных условий для линейной модели с использованием измеренных данных |
| Вы продолжаете моделирование, например, для онлайн-обработки. Используется разделенный набор данных, например, для nlarx модель, когда findstates слишком дорого в вычислительном отношении. | data2state
Если исходная модель idtf, idproc, или idpoly, сначала преобразовать в форму state-space с помощью idss. Также можно использовать data2state неявно путем указания ваших прошлых данных в качестве прокси для начальных условий при использовании sim или predict с любой динамической моделью.Дополнительные сведения см. в разделе Оценка начальных условий по измеренным данным. | sys_ss = idss(sys)x0 = data2state(sys,z_p)или IO = struct или opt = predictOptions ('InitialCondition',IO). примеры: Оценка начальных условий для нелинейной модели ARX, Понимание использования исторических данных для моделирования модели |
| При продолжении моделирования необходимо создать исходные условия для текущего сегмента моделирования на основе предыдущего сегмента. Вы намерены начать основное моделирование в установившемся состоянии, и вы хотите иметь приквел, который моделирует подготовку к установившемуся состоянию с отдыха. | Используйте сведения о состоянии из предыдущего моделирования или председательствования. Если исходная модель idtf, idproc, или idpoly, сначала преобразовать в форму state-space с помощью idss. Дополнительные сведения см. в разделе Использование начальных условий из информации о прошлом состоянии. | sys_ss = idss(sys)x0 = x(end) от [y,y_sd,x] = sim(sys_ss,z_p)Пример: Продолжение моделирования идентифицированной модели с использованием прошлых состояний |
В предыдущей таблице приводятся различные методы оценки начальных условий. В следующих разделах эти методы суммируются по источнику данных оценки.
Оцените исходные условия на основе данных измерений, из которых вы получаете входные данные моделирования. Методы включают в себя следующее.
Извлеките начальные условия из результатов идентификации модели, например, из отчета об идентификации модели или возвращенных значений из compare. X0 представляет вектор начального состояния, а IC представляет initialCondition объект. Примеры см. в разделах Разрешение различий значений соответствия между идентификацией модели и командой сравнения, Сопоставление выходных данных команды сравнения и нелинейного блока модели ARX и Применение начальных условий при моделировании идентифицированных линейных моделей.
Оценка начальных условий с использованием измеренных входных/выходных данных с использованием функции findstates для оценки начальных состояний, согласующихся с набором данных. Пример см. в разделе Оценка начальных условий для линейной модели с использованием измеренных данных.
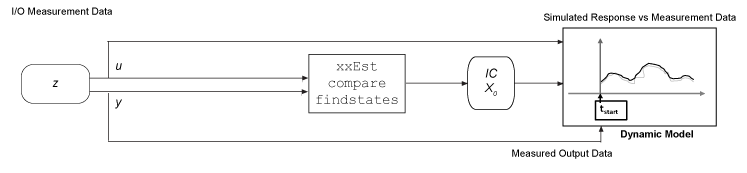
Оцените исходные условия по данным измерений непосредственно перед началом моделирования. Методы включают в себя следующее.
Использование функции data2state для оценки конечного состояния набора данных. Прошлое конечное состояние становится начальным состоянием для последующего моделирования. Пример см. в разделе Оценка начальных условий для нелинейной модели ARX.
Использование прошлых данных в качестве прокси для начальных условий при использовании sim или predict. При выполнении моделирования модель вызывает внутренний вызов data2state для тебя. Пример см. в разделе Понимание использования исторических данных для моделирования модели.
Разделение используемого набора данных на две части. Сделать первую часть достаточно большой, чтобы позволить data2state для вычисления точного конечного состояния. Такой подход разделения данных может быть гораздо менее ресурсоемким, чем использование findstates в полном наборе данных, особенно для нелинейных моделей ARX. Пример см. в разделе Оценка начальных условий для нелинейной модели ARX.
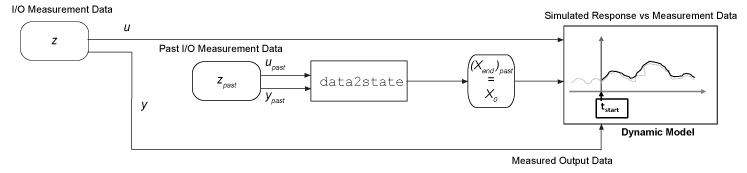
Использовать информацию о состоянии из предыдущего моделирования или председательствования. Если предыдущее моделирование недоступно, можно выполнить предоплату из состояния покоя или известного начального условия до момента начала моделирования. Конечные состояния прошлого или предоплаты являются начальными состояниями для моделирования, которое требуется выполнить. Пример см. в разделе Продолжение моделирования идентифицированной модели с использованием прошлых состояний.
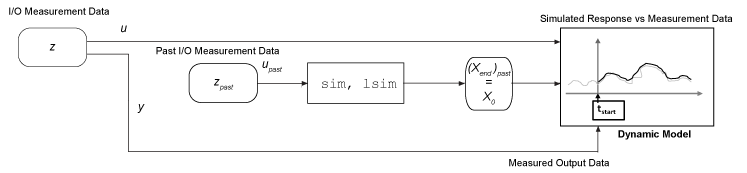
findstates и data2state функции являются наиболее общими инструментами для определения начальных или конечных состояний по любым измерениям входных/выходных данных. Однако для использования этих функций необходимо иметь структуру модели, которая включает явное представление состояния. Линейные модели, отличные от idss и idgrey не используйте явные состояния. Чтобы найти эквивалентные начальные состояния, можно преобразовать эти модели в idss модели и найти начальные состояния из idss версии. В качестве альтернативы findstates, вы также можете использовать compare для получения исходных условий без преобразования моделей в форму state-space. Для этих моделей: compare возвращает initialCondition объект, содержащий информацию о свободном ответе модели в форме state-space и соответствующих начальных состояниях.
После оценки начальных условий их можно включить в синтаксис моделирования командной строки, модель Simulink ® или приложение «Идентификация системы».
Следующие примеры иллюстрируют оценку начальных условий для линейных моделей. Первый пример использует findstates и compare. Во втором и третьем примерах используются исторические данные. То есть примеры определяют начальные условия из данных, непосредственно предшествующих времени начала моделирования.
Используйте различные методы, чтобы получить начальные условия для линейной модели и сравнить результаты.
Оценка передаточной функции для измеренных данных. Возврат начальных условий в ic.
load iddata1 z1; [sys,ic] = tfest(z1,3); ic
ic =
initialCondition with properties:
A: [3x3 double]
X0: [3x1 double]
C: [0.2303 5.9117 2.2283]
Ts: 0
ic.X0
ans = 3×1
-1.7569
2.6195
-6.5177
sys является определяемой передаточной функцией непрерывного времени (idtf) модель. ic является initialCondition объект. Один initialCondition объект представляет свободный отклик системы в форме state-space. Объект включает преобразованные A и C матрицы state-space, которые соответствуют sys и оцененный вектор начального состояния X0.
Также можно использовать findstates найти исходные условия для линейных моделей, но только если они находятся в idss или idgrey форма.
Новообращенный sys в форму state-space.
sys_ss = idss(sys);
Использовать findstates для оценки начальных состояний.
X0 = findstates(sys_ss,z1)
X0 = 3×1
-1.7569
2.6195
-6.5177
Теперь используйте compare для оценки начальных состояний с использованием исходной модели передаточной функции.
[y_tf,fit,ic2] = compare(z1,sys); ic2
ic2 =
initialCondition with properties:
A: [3x3 double]
X0: [3x1 double]
C: [0.2303 5.9117 2.2283]
Ts: 0
ic2.X0
ans = 3×1
-1.7569
2.6195
-6.5177
Во всех трех случаях векторы начального состояния идентичны.
Используйте исторические данные ввода-вывода в качестве прокси для начальных условий при моделировании модели. Сначала необходимо смоделировать с помощью sim и укажите исторические данные с помощью simOptions набор опций. Затем смоделированные выходные данные воспроизводятся путем сопоставления исторических данных с начальными состояниями вручную.
Загрузите набор данных с двумя входами и одним выходом.
load iddata7 z7
Определение модели пространства состояния пятого порядка с использованием данных.
sys = n4sid(z7,5);
Разбейте набор данных на две части.
zA = z7(1:15); zB = z7(16:end);
Моделирование модели с использованием входного сигнала в zB.
uSim = zB;
Для моделирования требуются начальные условия. Значения сигнала в zA являются историческими данными, то есть они являются входными и выходными значениями для времени, непосредственно предшествующего данным в zB. Использовать zA в качестве прокси для требуемых начальных условий.
IO = struct('Input',zA.InputData,'Output',zA.OutputData); opt = simOptions('InitialCondition',IO);
Моделирование модели.
ysim = sim(sys,uSim,opt);
Теперь воспроизведите выходные данные, вручную сопоставив исторические данные начальным состояниям sys. Для этого используйте data2state команда.
xf = data2state(sys,zA);
xf содержит значения состояния sys в момент непосредственно после последней выборки данных в zA.
Моделирование системы с помощью xf в качестве начальных состояний.
opt2 = simOptions('InitialCondition',xf);
ysim2 = sim(sys,uSim,opt2);Постройте график выходных данных sim команда ysim и вычисленные вручную результаты ysim2.
plot(ysim,'b',ysim2,'--r')

ysim2 является таким же, как ysim.
Оцените начальные условия для сегмента моделирования идентифицированной модели, используя конечные состояния предыдущего сегмента моделирования.
Загрузить данные z1, которые являются iddata объект, содержащий входные и выходные данные. Оцените линейную модель пятого порядка на основе данных.
load iddata1 z1 plot(z1)

sys = n4sid(z1,5);
Разделите данные на два сегмента. Один сегмент z1past представляет данные для предыдущего моделирования и начинается с восстановления. Второй сегмент z1next представляет данные для последующего моделирования.
z1past = z1(1:150); z1next = z1(150:300);
Моделирование ответа на входные данные в z1next без указания исходных условий.
ynext_no_ic = sim(z1next,sys);
plot(ynext_no_ic,z1next)
legend
title('Simulation Continuation Without Setting ICs')
Теперь определите конечные состояния, x0, для ответа на z1past вход.
[ypast,y_sd,xpast] = sim(z1past,sys); x0 = xpast(end,:)';
Используйте конечные состояния, чтобы указать начальные состояния для последующего ответа на z1next.
opt = simOptions('InitialCondition',x0); ynext_ic = sim(z1next,sys,opt); figure plot(ynext_ic,z1next) legend title('Simulation Continuation with Sychronized ICs')

При моделировании модели Hammerstein-Wiener или нелинейной серой коробки необходимо использовать начальные условия, соответствующие набору данных измерений z, использовать findstates.
Сравните моделируемый выходной сигнал блока модели Хаммерштейна-Винера с измеренным выходным сигналом системы. Согласование между измеренными и смоделированными откликами улучшается путем оценки начальных значений состояния.
Загрузите образцы данных.
load twotankdata
Создание iddata объект из образца данных. Набор 'Tstart' до 0, чтобы время начала данных соответствовало времени начала Simulink 0f 0 с.
z1 = iddata(y,u,0.2,'Tstart',0,'Name','Two tank system');
Оцените модель Хаммерштейна-Винера, используя данные.
mw1 = nlhw(z1,[1 5 3],pwlinear,pwlinear);
Теперь можно моделировать выходные данные расчетной модели в Simulink с помощью входных данных в z1. Для этого откройте предварительно настроенную модель Simulink.
model = 'ex_idnlhw_block';
open_system(model);

В модели используются блоки Iddata Source, Hammerstein-Wiener Model и Scope. Следующие параметры блока предварительно сконфигурированы для определения оценочных данных, оценочной модели и начальных условий:
Параметры блока источника Iddata:
Объект IDDATA - z1
Параметры блока модели Хаммерштейна-Винера:
Модель - mw1
Исходные условия - Zero (по умолчанию)
Запустите моделирование.
Просмотрите разницу между измеренными выходными данными и выходными данными модели с помощью блока «Область».
simOut = sim(model);
open_system([model '/Scope'])

Чтобы улучшить согласование между измеренными и смоделированными откликами, оцените вектор начального состояния для модели на основе данных оценки. z1, использование findstates. Укажите максимальное количество итераций для оценки как 100. Укажите горизонт прогнозирования как Inf, так что алгоритм вычисляет начальные состояния, которые минимизируют ошибку моделирования.
opt = findstatesOptions; opt.SearchOptions.MaxIterations = 100; x0 = findstates(mw1,z1,Inf,opt);
Установите значение параметра Initial conditions block блока Hammerstein-Wiener Model в значение State Values. Начальные состояния по умолчанию: x0.
set_param([model '/Hammerstein-Wiener Model'],'IC','State values');
Снова запустите моделирование и просмотрите разницу между измеренными выходными данными и выходными данными модели в блоке «Область». Теперь разница между измеренными и смоделированными откликами уменьшается.
simOut = sim(model);

При моделировании нелинейной модели ARX требуется использовать начальные условия, соответствующие набору данных измерений. z, у вас есть выбор для какого подхода.
Вы можете использовать findstates. Однако для нелинейных моделей ARX этот подход имеет стоимость вычислительной стоимости, если набор данных большой.
X0 = findstates(m,z,Inf);
Набор данных можно разбить на две части. Использовать первый nx выборки входных/выходных данных как прошлых данных, где nx является самой большой задержкой регрессора в модели. Затем использовать data2state для вычисления конечного состояния «прошлых данных». Затем можно смоделировать модель для оставшихся nx+1:end ввод данных с использованием любого выбранного метода моделирования. Оба compare и приложение System Identification использует этот подход автоматически для нелинейных моделей ARX.
nx = max(getDelayInfo(m)); % Find the largest regressor delay
past_data = z1(1:nx);
X0 = data2state(mw1,z1(1:nx));Следующий пример иллюстрирует использование метода разделения данных для нелинейной модели ARX.
Используйте два различных метода для оценки начальных условий нелинейной модели ARX. Моделирование каждого вместе с данными измерений и сравнение с моделированием, инициализируемым в состоянии покоя.
Загрузка входных/выходных данных z и постройте его. Используйте первые 1000 баллов z для оценки нелинейной модели ARX.
load twotankdata z = iddata(y,u,0.2); z1 = z(1:1000); plot(z1) title('Estimation data')

mdlnlarx = nlarx(z1,[5 1 3],wavenet);
Извлеките первые 250 точек z1 (50 секунд) как z1sim для сравнительного моделирования. Моделировать mdlarx без установки начальных условий и постройте график отклика вместе с измеренным выходом в z1sim.
z1sim = z1(1:250); data_no_ic = sim(mdlnlarx,z1sim); plot(data_no_ic,z1sim) title('Nonlinear ARX Model with No Initial Condition Setting') grid on legend('location','se')

Использовать findstates для оценки начальных условий. Чтобы минимизировать ошибку моделирования, укажите Inf для горизонта прогнозирования. Затем установите sim опция для InitialCondition в findstates результаты. Постройте график отклика вместе с измеренным выходным сигналом.
x0fs = findstates(mdlnlarx,z1sim,Inf); opt = simOptions('InitialCondition',x0fs); data_fs = sim(mdlnlarx,z1sim,opt); figure plot(data_fs,z1sim) title('Nonlinear ARX Model with IC Estimation Using findstates') grid on legend('location','se')

Отклик и измеренный выходной сигнал начинаются примерно в одной и той же точке.
Теперь используйте data2states способ оценки исходных условий. Сначала разбейте набор данных на две части. Использовать первый nx образцы z1sim как «прошлые данные», где nx является самой большой задержкой регрессора в модели.
nx = max(getDelayInfo(mdlnlarx))
nx = 5
z1past = z1sim(1:nx); z1sim2 = z1sim(nx+1:end);
Использовать data2state для вычисления конечного состояния «прошлых данных». Моделирование ответа с использованием входных данных, начиная с z1sim(nx+1). Постройте график ответа вместе с полным z1sim данные измерений, чтобы можно было сравнить с findstates график.
x0d2s = data2state(mdlnlarx,z1past); opt = simOptions('InitialCondition',x0d2s); data_d2s = sim(mdlnlarx,z1sim2,opt); figure plot(data_d2s,z1sim) title('Nonlinear ARX Model with IC Estimation Using data2state') grid on legend('location','se')

Если вы выполнили каждый раздел отдельно, вы можете обнаружить, что data2states метод завершен быстрее, чем findstates способ.
Теперь сравните ответы для всех трех случаев начального состояния.
plot(data_fs,data_d2s,data_no_ic) title('Nonlinear ARX model Responses for Three IC Approaches Compared') legend('location','se')

Ответы для случаев использования findstates и data2state практически одинаковы. Реакция на случай, когда исходные условия не были установлены, в конечном счете сходится, но только через 30 секунд.
compare | compareOptions | data2state | findstates | predict | predictOptions | sim | simOptions