Моделирование ответа идентифицированной модели
sim(___) строит график смоделированного отклика идентифицированной модели.
Когда исходные условия оцененной модели и системы, которая измеряла набор данных проверки, различны, смоделированные и измеренные ответы также могут отличаться, особенно в начале ответа. Чтобы минимизировать эту разницу, оцените начальные значения состояния с помощью findstates и используйте оценочные значения для установки InitialCondition опция с использованием simOptions. Пример см. в разделе Сопоставление ответа модели с выходными данными.
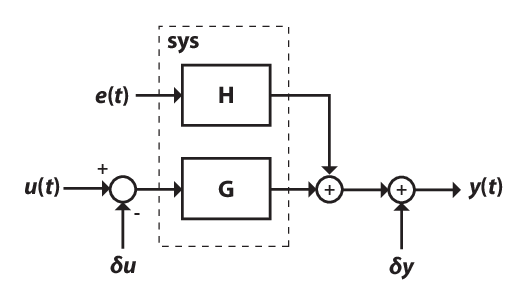
Моделирование означает вычисление отклика модели с использованием входных данных и исходных условий. sim моделирует следующую систему:
Здесь,
u (t) - входные данные моделирования ,udata.
y (t) - смоделированный выходной отклик.
G - передаточная функция от входа к выходу и определяется в sys. Исходные условия моделирования, указанные с помощью simOptions, установить исходное состояние G.
e (t) является необязательным шумовым сигналом. Добавление шума в моделирование путем создания simOptions набор опций и установка AddNoise опция для true. Кроме того, можно изменить шумовой сигнал по умолчанию, указав NoiseData вариант.
H является функцией передачи шума и определяется в sys.
δu - необязательный входной сдвиг, вычитаемый из входного сигнала u (t) до того, как вход будет использован для моделирования модели. Задайте смещение ввода, задав значение InputOffset опция с использованием simOptions.
δy - необязательный выходной сдвиг, добавляемый к выходному отклику y (t) после моделирования. Задайте смещение вывода, задав значениеOutputOffset опция с использованием simOptions.
Дополнительные сведения о задании начальных условий моделирования, входных и выходных смещений и данных шумового сигнала см. в разделе simOptions. Для многоэкспериментных данных можно задать эти опции отдельно для каждого эксперимента.
Использовать simsd для метода Монте-Карло вычисления стандартного отклонения отклика.
sim простирается lsim для облегчения дополнительных функций, относящихся к определенным моделям:
Моделирование нелинейных моделей
Моделирование с аддитивным шумом
Включение смещений сигналов
Вычисление стандартного отклонения отклика (только линейные модели)
Моделирование частотной области (только линейные модели)
Моделирование с использованием различных методов интерсамплирования для различных входных данных
Чтобы получить смоделированный ответ без какой-либо из предыдущих операций, используйте lsim.
compare | findstates | forecast | idinput | lsim | predict | simOptions | simsd | step