Представление начального условия для линейных инвариантных по времени систем
Один initialCondition объект инкапсулирует информацию начального условия для линейной инвариантной по времени (LTI) модели. Объект обобщает числовое векторное представление начальных состояний модели state-space так, чтобы информация применялась к линейным моделям любого вида - передаточным функциям, полиномиальным моделям или моделям state-space.
Можно оценить и извлечь начальные условия при определении линейной модели с помощью таких команд, как tfest или сравнить отклик модели с измеренными входными/выходными данными, используя compare. Программное обеспечение оценивает начальное значение условия путем минимизации ошибки моделирования или прогнозирования по измеренным выходным данным. Затем можно применить эти начальные условия в последующем моделировании с помощью таких команд, как sim или predict, для подтверждения производительности модели в отношении одних и тех же данных измерений. Используйте initialCondition для создания initialCondition объект из спецификации модели state-space или из любой модели LTI свободного отклика.
initialCondition объект также можно рассматривать как представление свободной реакции линейной модели. Функции моделирования используют эту информацию для вычисления отклика модели следующим образом:
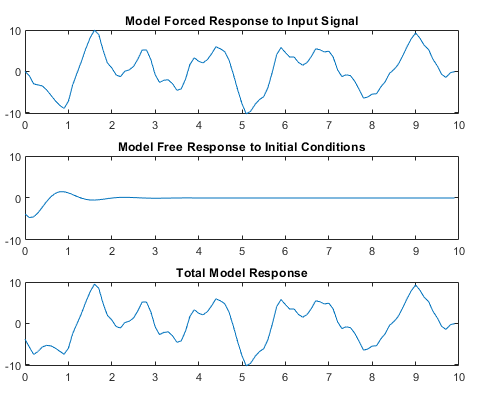
Вычислите принудительный отклик модели на входной сигнал. Принудительный отклик - это стандартный результат моделирования при отсутствии заданных начальных условий.
Вычислите импульсную характеристику модели и масштабируйте результат, чтобы создать свободную характеристику модели для заданных начальных условий.
Добавьте принудительный отклик и свободный отклик вместе, чтобы сформировать полный отклик системы.
Рисунок иллюстрирует этот процесс.
Для непрерывных систем (Ts = 0) свободный ответ G (s) для вектора x0 начального состояния равен
A) − 1x0
Здесь С эквивалентно матрице С измерения состояния-пространства, а а А эквивалентно матрице А измерения состояния-пространства.
Для дискретных систем (Ts > 0) свободный отклик G (z) равен
A) − 1x0
initialCondition объект представляет свободный ответ в форме state-space. Объект представляет собой структуру со свойствами, содержащими матрицы state-space A и C и вектор начального состояния x0. Для idtf и idpoly модели, с использованием initialCondition объект является единственным способом представления и использования исходных условий для моделирования. Для idss модели, можно использовать либо initialCondition объект или числовой вектор начального состояния. При получении исходных условий ic для многоэкспериментных данных, ic - массив объектов, с одним initialCondition объект для каждого эксперимента.
Вы можете получить initialCondition объект одним из четырех способов.
Оценка модели - определяет, что функция оценки возвращает оцененное начальное условие, которое соответствует входным/выходным данным оценки. Например, для получения расчетного начального условия можно использовать следующую команду: ic для модели передаточной функции sys которая оценивается с использованием входных/выходных данных z.
[sys,ic] = tfest(z,2,1)
Сравнение модели с данными с использованием любых входных/выходных данных - укажите, что compare вернуть предполагаемое начальное условие, которое функция оценивает внутри для поддержки fit оценка. Например, для получения начального условия можно использовать следующую команду: ic для линейной модели sys при определении соответствия входным/выходным данным z. yp - моделируемый или прогнозируемый выход модели.
[yp,fit,ic] = compare(z,sys)
Прямая конструкция - Используйте initialCondition команда для инкапсуляции формы state-space модели свободного отклика в initialCondition объект.
ic = initialCondition(A,X0,C,Ts)
Преобразование модели свободного ответа - используйте initialCondition команда для преобразования модели свободного отклика LTI в initialCondition объект.
ic = initialCondition(G)
Пример см. в разделе Преобразование модели Free-Response в объект initityCondition.
Сведения о функциях, которые можно использовать для извлечения информации из или преобразования initialCondition см. раздел Функции объектов.
ic = initialCondition(A,X0,C,Ts)initialCondition объект, представляющий свободный ответ на начальное условие, выраженное в форме state-space, модели LTI.
0) = x0
ic сохраняет эту модель в виде свойств. A и C соответствуют государственно-пространственной реализации модели, X0 к вектору исходного состояния x0, и Ts к времени выборки. Вы можете использовать ic задание начальных условий при моделировании любого типа системы LTI.
Функции, применимые к initialCondition это объекты, которые могут возвращать, использовать или преобразовывать объекты.
| Роль начального условия (IC) | Тип функции LTI | Пример синтаксиса | Примеры ссылок |
|---|---|---|---|
| Возврат оцененных объектов IC | Все функции оценки, compare | [sys,ic] = tfest(data,2,1) | Получение расчетных начальных условий |
| Использование объектов IC для реакции модели | Наборы опций для функций ответа модели | opt = simOptions('InitialCondition',ic) | Применение начальных условий в моделировании |
| Преобразование объектов IC в динамические системные модели (DSM) | Функции объекта DSM | g = idtf(ic) | Визуализация свободного ответа на исходное условие |
| Анализ моделей, преобразованных из объектов IC | Функции анализа DSM | y_g = impulse(g) | Визуализация свободного ответа на исходное условие |
Оцените модель передаточной функции и получите расчетные начальные условия.
Загрузите и постройте график данных.
load iddata1ic.mat z1i plot(z1i)
Выходные данные не начинаются с 0.
Оценка функции переноса по второму заказу sys_tf. Укажите, что функция возвращает начальные условия ic.
[sys_tf,ic] = tfest(z1i,2,1);
Изучить содержание ic. ic включает в себя в форме state-space модель свободного отклика, определяемую матрицами A и C, вектор начального состояния X0и время выборки Ts.
A = ic.A
A = 2×2
-2.9841 -5.5848
4.0000 0
C = ic.C
C = 1×2
0.2957 5.2441
x0 = ic.X0
x0 = 2×1
-0.9019
-0.6161
Ts = ic.Ts
Ts = 0
ic специфичен для данных оценки z1i. Вы можете использовать ic для установки начальных условий при моделировании любой модели LTI с использованием входного сигнала от z1i и сравнить ответ с z1i выходной сигнал.
Визуализация свободного ответа, инкапсулированного в initialCondition объект путем формирования импульсной характеристики.
Оценка передаточной функции и возврат исходного условия ic_tf.
load iddata1ic z1i [sys_tf,ic_tf] = tfest(z1i,2,1); ic_tf
ic_tf =
initialCondition with properties:
A: [2x2 double]
X0: [2x1 double]
C: [0.2957 5.2441]
Ts: 0
ic_tf содержит информацию, необходимую для вычисления свободного ответа на начальное условие.
Новообращенный ic_tf в idss объект, который может быть передан impulse функция.
ic_tfss = idss(ic_tf);
Создание вектора времени t который охватывает набор данных. Вычислите импульсную характеристику.
t = 0:0.1:9.9;
t = t';
yimp = impulse(ic_tfss,t);
plot(t,yimp)
title('Free Response to Initial Condition')
Свободный ответ - это переходный процесс, который длится около четырех секунд.
Загрузка данных и оценка функции переноса второго заказа sys. Вернуть начальные условия в ic.
load iddata1ic z1i [sys,ic] = tfest(z1i,2,1);
Моделировать sys использование оценочных данных, но без включения исходного условия. Постройте график смоделированного выходного сигнала с измеренным выходным сигналом.
y_no_ic = sim(sys,z1i); plot(y_no_ic,z1i) legend('Model Response','Measured Output')
Измеренные и смоделированные выходные данные не согласуются в начале моделирования.
Соединиться ic в simOptions набор опций opt. Моделирование и печать отклика модели с помощью opt.
opt = simOptions('InitialCondition',ic); y_ic = sim(sys,z1i,opt); plot(y_ic,z1i); legend('Model Response','Measured Output')
Моделирование объединяет отклик модели на входной сигнал со свободным откликом на исходное условие. Измеренные и смоделированные результаты теперь лучше согласуются в начале моделирования.
Предполагаемое initialCondition объект специфичен для данных, по которым он был оценен. Для моделирования модели с использованием новых данных, таких как данные проверки, необходимо оценить новое начальное условие для этих данных. Для этого используйте compare команда.
Загрузите данные и разбейте их на наборы данных оценки и проверки.
load iddata1 z1 z1_est = z1(1:150); z1_val = z1(151:300); plot(z1_est,z1_val); legend('Estimation Data','Validation Data')
Проверьте начальные точки каждого набора выходных данных.
e0 = z1_est.y(1)
e0 = -0.5872
v0 = z1_val.y(1)
v0 = -7.4390
Два набора данных имеют разные начальные условия.
Оценка модели функции переноса второго заказа с использованием z1_est. Вернуть предполагаемые начальные условия в ic_est. Отображение X0 имущество ic_est. Это свойство представляет оцененный вектор начального состояния, определенный моделью свободного ответа ic_est.A и ic_est.C отвечает.
[sys,ic_est] = tfest(z1_est,2,1); ic_est.X0
ans = 2×1
-0.4082
0.0095
Вы можете использовать ic_est если вы хотите смоделировать sys использование z1_est. Кроме того, можно использовать compare, которая оценивает исходное состояние независимо. Использовать compare дважды, один раз для построения графика данных и один раз для возврата результатов. Отображение вектора начального состояния ic_estc.X0 это compare оценки.
compare(z1_est,sys)
[yce,fit,ic_estc] = compare(z1_est,sys); ic_estc.X0
ans = 2×1
-0.4082
0.0095
Вектор начального состояния ic_estc.X0 идентичен ic_est.
Теперь проанализируйте модель с помощью набора данных проверки. Оцените начальные условия с помощью данных проверки.
compare(z1_val,sys)
[ycv,fit,ic_valc] = compare(z1_val,sys); ic_valc.X0
ans = 2×1
-1.7536
-0.9547
Вы можете использовать ic_val при моделировании sys с z1_val входной сигнал и сравните отклик модели на z1_val выходной сигнал.
Оценка initialCondition объектный массив с использованием данных мультиэксперимента.
Загрузить данные из двух экспериментов. Объедините два набора данных в один многоцелевой набор данных.
load iddata1 z1 load iddata2 z2 z12 = merge(z1,z2)
z12 =
Time domain data set containing 2 experiments.
Experiment Samples Sample Time
Exp1 300 0.1
Exp2 400 0.1
Outputs Unit (if specified)
y1
Inputs Unit (if specified)
u1
plot(z12)
Оценка функции переноса второго заказа sys и вернуть начальные условия в ic.
np = 2; nz = 1; [sys,ic] = tfest(z12,np,nz); ic
ic=1×2 object
1x2 initialCondition array with properties:
A
X0
C
Ts
ic является массивом объектов. Отображение содержимого каждого объекта.
ic(1,1)
ans =
initialCondition with properties:
A: [2x2 double]
X0: [2x1 double]
C: [-0.7814 5.2530]
Ts: 0
ic(1,2)
ans =
initialCondition with properties:
A: [2x2 double]
X0: [2x1 double]
C: [-0.7814 5.2530]
Ts: 0
Сравните A, X0, и C для каждого объекта.
A1 = ic(1,1).A
A1 = 2×2
-3.4824 -5.5785
4.0000 0
A2 = ic(1,2).A
A2 = 2×2
-3.4824 -5.5785
4.0000 0
C1 = ic(1,1).C
C1 = 1×2
-0.7814 5.2530
C2 = ic(1,2).C
C2 = 1×2
-0.7814 5.2530
X01 =ic(1,1).X0
X01 = 2×1
-0.6528
-0.0067
X02 =ic(1,2).X0
X02 = 2×1
0.3076
-0.0715
A и C матрицы идентичны. Эти матрицы представляют форму «состояние-пространство» sys. X0 векторы различны. Это различие является результатом различных начальных условий для двух экспериментов.
initialCondition Объект из модели State-SpaceОцените модель «состояние-пространство» и верните начальные состояния. На основе модели и вектора начального состояния создайте initialCondition объект, который можно использовать с любой линейной моделью.
Загрузите и постройте график данных.
load iddata1ic z1i plot(z1i)
Оцените модель состояния-пространства и получите предполагаемые начальные условия.
Сначала установите 'InitialState' аргумент пары имя-значение в ssestOptions кому 'estimate', которая переопределяет настройку по умолчанию 'auto'. 'estimate' установка всегда оценивает начальные состояния. 'auto' установка использует 'zero' установка, если влияние начальных состояний на общую ошибку оценки модели относительно мало, и, следовательно, может привести к вектору начального состояния, содержащему только нули.
opt = ssestOptions; opt = ssestOptions('InitialState','estimate');
Оценка модели пространства состояния второго порядка sys_ss. Укажите выходной аргумент x0 для возврата вектора начального состояния. Укажите входной аргумент opt для использованияInitialState' установка. После оценки осмотрите x0.
[sys_ss,x0] = ssest(z1i,2,opt); x0
x0 = 2×1
0.0631
0.0329
x0 - ненулевой вектор начального состояния.
Моделирование модели с помощью x0 и сравнивают выходные данные с исходными выходными данными.
Использовать x0 в качестве начального условия укажите 'InitialCondition' аргумент пары имя-значение в simOptions как x0.
opt = simOptions;
opt = simOptions('InitialCondition',x0);Моделирование модели с помощью opt и сохранить ответ в xss.
xss = sim(sys_ss,z1i,opt);
Постройте график отклика модели с исходными выходными данными.
t = 0:0.1:19.9; plot(t',[xss.y z1i.y]) legend('ss model','output data') title('Simulated State-Space Model Using Estimated Initial States')
Моделирование начинается в точке, близкой к начальной точке данных.
С помощью A и C матрицы, x0и время выборки Ts от sys_ss, построить initialCondition объект ic который можно использовать с моделью передаточной функции.
A = sys_ss.A; C = sys_ss.C; Ts = sys_ss.Ts; ic = initialCondition(A,x0,C,Ts)
ic =
initialCondition with properties:
A: [2x2 double]
X0: [2x1 double]
C: [-61.3674 13.4811]
Ts: 0
Оценка модели передаточной функции и моделирование модели с помощью ic в качестве начального условия. Сохранить ответ в xtf.
sys_tf = tfest(z1i,2,1);
opt = simOptions('InitialCondition',ic);
xtf = sim(sys_tf,z1i,opt);Постройте график откликов модели xss и xtf вместе.
plot(t',[xss.y xtf.y]) legend('ss model','tf model') title('Simulated SS and TF Models with Equivalent Initial Conditions')
Модели тщательно отслеживают друг друга на протяжении всего моделирования.
initialCondition ОбъектПолучение исходных условий при оценке модели передаточной функции. Преобразовать initialCondition в модель свободного ответа и модель свободного ответа обратно в initialCondition объект.
Загрузка данных и оценка модели передаточной функции sys. Получение расчетных исходных условий ic.
load iddata1ic.mat z1i [sys,ic] = tfest(z1i,2,1);
Новообращенный ic в idtf модель свободного ответа g.
g = idtf(ic);
Постройте график импульсной характеристики g.
impulse(g)
title('Impulse Response of g')
Новообращенный g обратно в initialCondition объект ic1.
ic1 = initialCondition(g);
Постройте график импульсной характеристики ic1 путем преобразования ic1 в idss модель.
impulse(idss(ic1))
title('Impulse Response of ic1 in idss form')
Импульсные реакции кажутся идентичными.
Выдержать сравнение ic и ic1.
ic.A
ans = 2×2
-2.9841 -5.5848
4.0000 0
ic1.A
ans = 2×2
-2.9841 -5.5848
4.0000 0
ic.X0
ans = 2×1
-0.9019
-0.6161
ic1.X0
ans = 2×1
4
0
ic.C
ans = 1×2
0.2957 5.2441
ic1.C
ans = 1×2
-0.8745 -1.7215
A матрицы ic и ic1 идентичны. C матрица и X0 векторы различны. Для данной линейной модели возможно бесконечно много представлений состояния-пространства. Эти два объекта эквивалентны, как показано импульсными откликами.
compare | impulse | polyest | predict | predictOptions | sim | simOptions | ssest | tfest