Преобразование изменения коэффициента усиления и фазы в изменение коэффициента усиления на основе диска
При анализе запаса диска коэффициент усиления и фазовые изменения моделируются как коэффициент F (s), умножающий отклик L (s) разомкнутого контура. Этот коэффициент принимает значения на диске D, центрированном по реальной оси с перехватами по реальной осиgmin и gmax. Поле диска определяет наибольший размер диска [gmin,gmax] для которого цикл обратной связи остается стабильным. Это обеспечивает запас усиления не менее DGM = [gmin,gmax] а также некоторый запас по фазе DPM определяется геометрией диска.
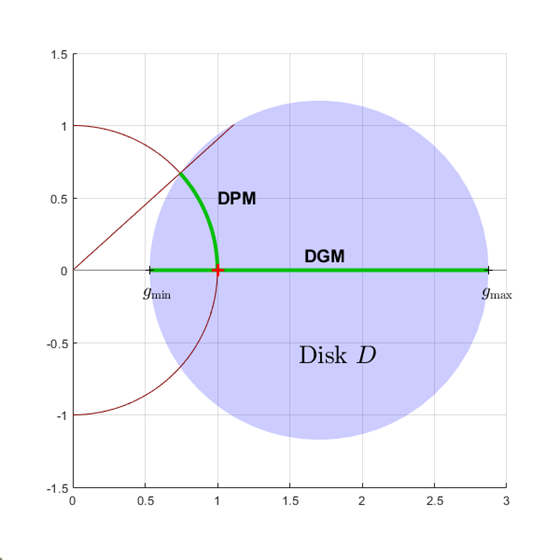
И наоборот, getDGM принимает желаемый коэффициент усиления и поля фаз GM и PM и вычисляет наименьший диск D, который доставляет и то, и другое. Этот диск характеризуется реальными осевыми перехватами gmin, gmax и соответствующий запас усиления на основе диска DGM = [gmin,gmax] и запас по фазе DPM встретиться или превысить GM и PM.
Дополнительные сведения о дисковой модели усиления и изменения фазы см. в разделе Алгоритмы.
DGM = getDGM(GM,PM,'tight')GM и PM.
Если GM и PM скаляры, то диск захватывает выигрыш, который может увеличиться или уменьшиться в раз GMи фаза, которая может увеличиться или уменьшиться на PM.
Если GM и PM являются векторами формы [glo,ghi] и [pmin,pmax] затем диск фиксирует относительные изменения усиления и фазы в этих диапазонах.
Если либо GM или PM является [], что снимает соответствующее ограничение на размер диска.
Выходные данные имеют вид DGM = [gmin,gmax]и описывает диск, который представляет абсолютные вариации усиления в этом диапазоне. Например, DGM = [0.8,1.8] коэффициент усиления моделей, который может изменяться от 0,8 номинального значения до 1,8 номинального значения, а фазовые изменения определяются геометрией диска. Этот диск может иметь ненулевой перекос (см. Алгоритмы). Использовать DGM для создания umargin блок, моделирующий эти изменения усиления и фазы.
Найдите наименьший запас усиления на основе диска, который представляет относительное изменение коэффициента усиления ± 6 дБ относительно номинального значения и изменения фазы ± 40 °. Преобразуйте изменение коэффициента усиления в абсолютные единицы.
GM = db2mag(6)
GM = 1.9953
PM = 40;
DGM = getDGM(GM,PM,'tight')DGM = 1×2
0.4299 1.9953
DGM описывает диск, моделирующий изменения усиления и фазы. Значения в DGM представляют диапазон вариаций усиления при отсутствии вариаций фазы. Обратите внимание, что DGM диапазон немного больше указанного [1/GM,GM] диапазон, поскольку требования к запасам по фазе являются более жесткими и определяют размер диска. Визуализация всего диапазона коэффициентов усиления и фазовых изменений, представленных DGM.
diskmarginplot(DGM)
'tight"ограничение вычисляет наименьший диск, который обеспечивает как целевое усиление, так и фазовые изменения, что не обязательно представляет симметричный диапазон усиления. В этом случае диск представляет выигрыш, который может уменьшиться несколько больше, чем может увеличиться. Изучить диск неопределенности, определенной именно этим DGM.
diskmarginplot(DGM,'disk')
Для обеспечения симметричного изменения коэффициента усиления используйте 'balanced' вариант.
Определите запас усиления на основе диска, который обеспечивает симметричное изменение усиления 5 дБ и изменение фазы ± 30 градусов.
GM = db2mag(5);
PM = 30;
DGM = getDGM(GM,PM,'balanced')DGM = 1×2
0.5623 1.7783
'balancedОграничение 'моделирует диск неопределенности, который симметричен относительно номинального значения. Функция возвращает симметричный запас усиления на основе диска DGM = [gmin,gmax], с gmin=1/gmax.
diskmarginplot(DGM)
В этом случае DPM немного превышает целевое изменение фазы и DGM равно целевому изменению коэффициента усиления.
Определите запас усиления на основе диска, соответствующий изменениям коэффициента усиления от 90% до 160% от номинального значения, и фазовым изменениям от -15 до + 15 градусов.
gainRange = [0.9,1.6];
phaseRange = [-15,15];
DGMt = getDGM(gainRange,phaseRange,'tight')DGMt = 1×2
0.8603 1.6000
'tightОграничение 'моделирует наименьший диск, который обеспечивает целевое усиление и фазовые изменения. Этот диск смоделирован с изменением коэффициента усиления, которое смещается в сторону увеличения коэффициента усиления.
Кроме того, можно использовать 'balanced«параметр, ограничивающий запас усиления на основе диска симметричным диапазоном формы» gmin = 1/gmax. Это означает, что коэффициент усиления может увеличиваться или уменьшаться на равную величину.
DGMb = getDGM(gainRange,phaseRange,'balanced')DGMb = 1×2
0.6250 1.6000
Визуализация диапазона одновременного усиления и фазовых изменений, соответствующих обоим диапазонам усиления.
diskmarginplot([DGMt;DGMb])
![Figure contains an axes. The axes with title Range of gain and phase variations contains 2 objects of type patch. These objects represent DGM = [0.86,1.6], DPM = 15, DGM = [0.625,1.6], DPM = 26.](../../examples/robust/win64/ComputeDiskMarginFromRangeOfGainAndPhaseVariationsExample_01.png)
Сбалансированный диапазон DGMb моделирует больший симметричный диапазон усиления (gmin = 1/gmax) и большие фазовые вариации, чем указанные вами. Если вы уверены, что выигрыш варьируется больше в одном направлении, чем в другом в вашей системе, то эта сбалансированная модель может быть чрезмерно консервативной.
Определите сбалансированные диапазоны запаса усиления на основе диска, которые обеспечивают вариации коэффициента усиления ± 4 дБ, ± 6 дБ и ± 12 дБ и изменение фазы ± 30 °. Можно получить все диапазоны усиления на основе диска одновременно, сложив требуемые целевые диапазоны в вектор столбца.
GM = db2mag([4;6;12]);
PM = 30;
DGM = getDGM(GM,PM,'balanced')DGM = 3×2
0.5774 1.7321
0.5012 1.9953
0.2512 3.9811
diskmarginplot(DGM)
![Figure contains an axes. The axes with title Range of gain and phase variations contains 3 objects of type patch. These objects represent DGM = [0.577,1.73], DPM = 30, DGM = [0.501,2], DPM = 36.8, DGM = [0.251,3.98], DPM = 61.8.](../../examples/robust/win64/DGMForMultipleTargetGainAndPhaseVariationsExample_01.png)
Каждая строка в матрице DGM дает изменение коэффициента усиления на основе диска для соответствующей записи в GM. Например, наименьший сбалансированный (симметричный) диск, который фиксирует изменение коэффициента усиления ± 4 дБ и изменение фазы ± 30 °, определяется DGM(1,:) = [0.58 1.73].
Этот диск представляет несколько больше, чем цель ± 4 дБ, чтобы захватить полную вариацию усиления цели ± 30 °. Для целей ± 6 дБ и ± 12 дБ диск точно отвечает изменению целевого коэффициента усиления, но соответствующие диски описывают большие изменения фазы.
DGM - Моделируемый диапазон изменения относительного коэффициента усиленияМоделируемый диапазон изменения относительного усиления, возвращаемый как двухэлементный вектор вида [gmin,gmax], где gmin < 1 и gmax > 1. Например, DGM = [0.8 1.5] представляет собой выигрыш, который может изменяться от 80% до 150% от его номинального значения (то есть изменяться на коэффициент от 0,8 до 1,5). gmin может быть отрицательным, определяя диапазон изменений относительного усиления, который включает в себя изменение знака. При использовании 'balanced' изменение коэффициента усиления симметрично, то есть коэффициент усиления может увеличиваться или уменьшаться на ту же величину (gmin = 1/gmax).
Диапазон [gmin,gmax] описывает диск усиления и фазовой неопределенности, где усиление может изменяться [gmin,gmax] и фаза может изменяться на величину, определяемую геометрией диска. Например, следующий график показывает диск, характеризующийся DGM = [0.5,2] (Дополнительные сведения о дисковой модели неопределенности см. в разделе Алгоритмы). Соответствующее изменение фазы (возвращается в DPM) равно ± 30 °.
![Uncertainty disk characterized by DGM = [0.5,2]](disk_dgm_argdesc.png)
В общем, DGM или соответствующее DPM может захватывать большие диапазоны вариаций, чем те, которые указаны при вводе GM и PM. Диск всегда фиксирует по крайней мере указанные варианты.
Если GM - вектор столбца или матрица, представляющая несколько целевых диапазонов изменения коэффициента усиления, DGM - двухстолбцовая матрица формы [gmin1,gmax1; ...;gminN,gmaxN], где каждая строка является соответствующим диапазоном усиления на основе диска.
DPM - Изменение фазы на основе дискаПоле фазы на основе диска, возвращаемое как двухэлементный вектор формы [-pm,pm]. Величина изменения фазы определяется геометрией диска, описанной DGM (см. Алгоритмы).
Если PM - вектор столбца или матрица, представляющая несколько целевых диапазонов изменения фазы, DPM - двухстолбцовая матрица формы [-pm1,pm1; ...;-pmN,pmN], где каждая строка является соответствующим диапазоном усиления на основе диска.
umargin и diskmargin моделируют усиление и фазовые изменения в отдельном канале обратной связи в качестве частотно-зависимого мультипликативного коэффициента F (s), умножающего номинальный отклик с разомкнутым контуром L (s), так что возмущенный отклик равен L (s) F (s). Коэффициент F (ы) параметризуется следующим образом:
В этой модели
δ (s) - динамическая неопределенность, ограниченная коэффициентом усиления, нормализованная таким образом, что она всегда изменяется в пределах единичного диска (||δ||∞ < 1).
ɑ устанавливает величину усиления и изменения фазы, смоделированную F. Для фиксированного λ параметр ɑ управляет размером диска. Для ɑ = 0 мультипликативный коэффициент равен 1, что соответствует номинальному L.
, называемый перекосом, смещает смоделированную неопределенность в сторону увеличения или уменьшения усиления.
Коэффициент F принимает значения на диске, центрированном по реальной оси и содержащем номинальное значение F = 1. Диск характеризуется своим перехватом DGM = [gmin,gmax] с действительной осью. gmin < 1 и gmin > 1 - минимальное и максимальное относительные изменения коэффициента усиления, смоделированные по F, на номинальной фазе. Фазовая неопределенность, смоделированная F, представляет собой диапазон DPM = [-pm,pm] фазовых значений при номинальном усилении (| F | = 1). Например, на следующем графике справа показан диск F, пересекающий действительную ось в интервале [0.71.1.4]. В левой части показано, что этот диск моделирует вариацию усиления ± 3 дБ и вариацию фазы ± 19 °.
DGM = [0.71,1.4]
F = umargin('F',DGM)
plot(F)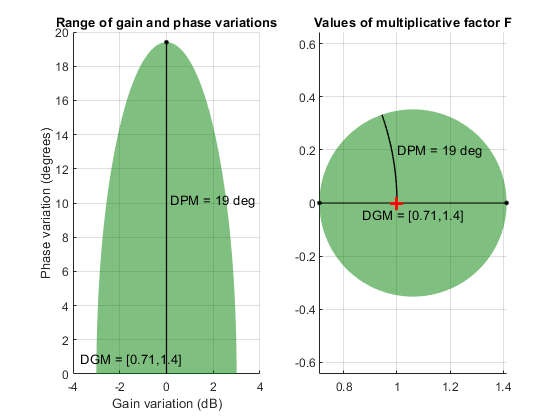
getDGM преобразует целевое усиление и изменения фазы, которые необходимо моделировать, в диапазон изменений усиления на основе диска DGM. Этот диапазон полностью характеризует диск F. Соответствующий диапазон фаз DPM таким образом, определяется DGM и модель диска.
Дополнительные сведения о модели неопределенности для изменений коэффициента усиления и фазы см. в разделе Анализ стабильности с использованием полей диска.