Усиление модели и фазовая неопределенность
Используйте umargin блок управления конструкцией для моделирования усиления и фазовых изменений в контурах обратной связи. Моделирование изменений коэффициента усиления и фазы в системе позволяет проверять пределы устойчивости при анализе надежности или применять их при проектировании надежных контроллеров.
Чтобы добавить коэффициент усиления и фазовую неопределенность в контур обратной связи, необходимо включить umargin блоки в неопределенное состояние-пространство (uss) модель системы замкнутого контура. umargin - блок управления SISO, представляющий изменение коэффициента усиления и фазы в одном местоположении в одном контуре обратной связи. Для моделирования усиления и фазовой неопределенности в системах обратной связи MIMO вставьте отдельный umargin объект в каждом местоположении системы, в котором требуется ввести коэффициент усиления и фазовую неопределенность.
umargin моделирует усиление и фазовые вариации как коэффициент F, умножающий отклик L. Этот коэффициент принимает значения на диске, центрированном по реальной оси и содержащем F = 1. Вы указываете этот диск по его пересечению DGM = [gmin,gmax] с действительной осью, которая представляет относительную величину изменения коэффициента усиления вокруг номинального значения F = 1. Чтобы задать как коэффициент усиления, так и фазовую неопределенность, сначала используйте getDGM для получения DGM значение, описывающее диск, который фиксирует как заданный диапазон усиления, так и диапазон фаз. Дополнительные сведения о дисковой модели неопределенности см. в разделе Алгоритмы.
Когда у вас есть uss модель, содержащая umargin управляющие блоки проектирования, можно выполнить анализ надежности и наихудшего случая, чтобы выяснить, как усиление и изменение фазы влияют на реакцию системы. Например, использовать robstab и robgain для анализа надежной стабильности и надежной производительности системы с неопределенностью коэффициента усиления и фазы. Использовать wcgain и wcsigmaplot для изучения наихудших ответов системы.
Требуется надежная стабильность для системы с замкнутым контуром с umargin коэффициент усиления и фазовая неопределенность эквивалентны обеспечению запаса усиления на основе дисков [gmin,gmax] и соответствующий запас фазы. Поэтому можно использовать umargin блоки для обеспечения подходящих полей диска при разработке надежных контроллеров с musyn.
F = umargin(name,DGM)DGM = [gmin,gmax] с gmin < 1 и gmax > 1. Коэффициент усиления, смоделированный F изменяется в этом диапазоне для фазы, удерживаемой при ее номинальном значении. Когда у вас есть и коэффициент усиления, и фазовая неопределенность, используйте getDGM для поиска соответствующего DGM. Этот синтаксис также устанавливает Name имущество F.
F = umargin(name,GM)umargin(name,[1/GM,GM]). Этот синтаксис задает коэффициент усиления, который может увеличиваться или уменьшаться GM при отсутствии фазовой неопределенности. Соответствующая величина фазовой неопределенности определяется дисковой моделью неопределенности, которая umargin использует (см. Алгоритмы).
F = umargin(___,Name,Value)F используя пары имя-значение. Например, F = umargin('F',[0.8,1.4],'InputName','u0','OutputName','u') создает umargin блок и задает входные и выходные имена для использования с connect. Заключите каждое имя свойства в кавычки.
Многие функции, которые работают с числовыми моделями LTI, также работают с неопределенными блоками проектирования управления, такими как umargin. К ним относятся функции взаимодействия моделей, такие как connect и feedbackи функции линейного анализа, такие как bode и stepinfo. Некоторые функции, генерирующие графики, такие как bode и step, постройте случайные выборки неопределенной модели, чтобы дать вам ощущение распределения неопределенной динамики. Однако при использовании этих команд для возврата данных они работают только на номинальном значении системы. Следующие списки содержат репрезентативное подмножество функций, которые можно использовать с umargin модели.
umargin моделирует изменения усиления и фазы в отдельном канале обратной связи в качестве частотно-зависимого мультипликативного коэффициента F (s), умножающего номинальный отклик с разомкнутым контуром L (s), так что возмущенный отклик равен L (s) F (s). Коэффициент F (ы) параметризуется следующим образом:
В этой модели
δ (s) - динамическая неопределенность, ограниченная коэффициентом усиления, нормализованная таким образом, что она всегда изменяется в пределах единичного диска (||δ||∞ < 1).
ɑ устанавливает величину усиления и изменения фазы, смоделированную F. Для фиксированного λ параметр ɑ управляет размером диска. Для ɑ = 0 мультипликативный коэффициент равен 1, что соответствует номинальному L.
, называемый перекосом, смещает смоделированную неопределенность в сторону увеличения или уменьшения усиления.
Коэффициент F принимает значения на диске, центрированном по реальной оси и содержащем номинальное значение F = 1. Диск характеризуется своим перехватом DGM = [gmin,gmax] с действительной осью. gmin < 1 и gmin > 1 - минимальное и максимальное относительные изменения коэффициента усиления, смоделированные по F, на номинальной фазе. Фазовая неопределенность, смоделированная F, представляет собой диапазон DPM = [pmin,pmax] фазовых значений при номинальном усилении (| F | = 1). Например, на следующем графике справа показан диск F, пересекающий действительную ось в интервале [0.71.1.4]. В левой части показано, что этот диск моделирует вариацию усиления ± 3 дБ и вариацию фазы ± 19 °.
F = umargin('F',1.4125)
plot(F)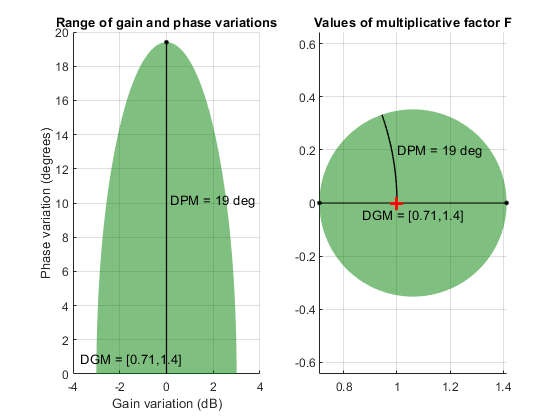
При создании umargin блок, степень неопределенности задается путем указания DGM. Использовать getDGM для преобразования определенных величин усиления и фазовых изменений в подходящую DGM диапазон, который фиксирует эти вариации. Для получения дополнительной информации о модели неопределенности, используемой umargin, см. Анализ стабильности с использованием полей диска.