Анализ стабильности с использованием полей диска

Дисковые поля количественно определяют стабильность системы с замкнутым контуром против усиления или фазовых изменений в отклике с разомкнутым контуром. В дисковых расчетах запаса программное обеспечение моделирует такие вариации, как дискообразная мультипликативная неопределенность функции передачи с разомкнутым контуром. Запас диска измеряет степень неопределенности, которую может выдержать цикл перед нестабильностью.

Эта величина неопределенности соответствует минимальному выигрышу и запасам по фазе. Дисковый запас усиления DGM - это величина, на которую коэффициент усиления цикла может увеличиваться или уменьшаться без потери стабильности в абсолютных единицах. Дисковый запас фазы DPM - это величина, на которую фаза цикла может увеличиваться или уменьшаться без потери стабильности, в градусах. Эти дисковые поля учитывают все частоты и взаимодействия контуров. Поэтому дисковый анализ запаса обеспечивает более надежную гарантию стабильности, чем классический коэффициент усиления и запас по фазе.

Надежное управление Toolbox™ предоставляет следующие инструменты:

Анализ стабильности системы по коэффициенту усиления и фазовым изменениям. Использовать diskmargin для вычисления коэффициента усиления на основе диска и полей фазы циклов обратной связи SISO и MIMO.
Коэффициент усиления модели и фазовая неопределенность. Используйте umargin блок управления для анализа влияния усиления и неопределенности на производительность и стабильность системы.

Моделирование усиления и фазовых изменений

Открыть сценарий в реальном времени

Оба umargin и diskmargin представлять коэффициент усиления и изменение фазы как мультипликативный комплексный коэффициент F (s), заменяющий номинальный отклик с разомкнутым контуром L (s) на L (s)*F (ы). Коэффициент F принимает значения на диске, который включает номинальное значение F = 1. Этот мультипликативный коэффициент моделирует как изменения усиления, так и фазы. Например, на следующем графике показан один такой диск в комплексной плоскости.

DGM = [0.6,1.7];
diskmarginplot(DGM,'disk')

Figure contains an axes. The axes with title Values of multiplicative factor F contains 8 objects of type patch, line, text.

Значения на этом диске охватывают только относительные изменения коэффициента усиления в диапазоне DGM = [0,6,1,7], или ± 4 дБ. Они также представляют абсолютные вариации только фазы DPM = [-29,29], или ± 29 °. Рассмотрим следующую систему замкнутого контура с номинальной передачей контура L и обратной связью блока.

Если этот цикл обратной связи остается стабильным для всех значений F на диске, показанных на предыдущем графике, то запас усиления на основе диска L составляет по меньшей мере DGM, и запас фазы на основе диска составляет по меньшей мере DPM.

Как умаргин, так и дискмаргин моделируют усиление и фазовую неопределенность с семейством дисков, описываемых двумя параметрами, α и λ. Для систем SISO диск параметризуется следующим образом:

$\frac{}{} F=1+α[(1-σ)/2]δ1-α[(1+σ)/2]δ.$

В этой модели

δ - нормированная неопределённость (произвольное комплексное значение в единичном диске | δ | < 1).
α задает величину усиления и изменения фазы, смоделированную F. Для фиксированного λ параметр α управляет размером диска. Для α = 0 мультипликативный коэффициент равен 1, что соответствует номинальному L.
, называемый перекосом, смещает смоделированную неопределенность в сторону увеличения или уменьшения усиления.

Каждая пара α, λ соответствует диску, который моделирует конкретный диапазон изменения усиления DGM = [gmin, gmax], задаваемый точками, где диск перехватывает действительную (x) ось. Соответствующее изменение фазы DPM определяется углом между действительной осью и линией через начало координат и касательную к диску. Таким образом, вы можете описать смоделированное множество коэффициентов усиления и фазовых вариаций полностью либо двумя значениями α, λ, либо двумя значениями DGM = [gmin, gmax]. λ = 0 моделирует сбалансированное изменение коэффициента усиления с [gmin, gmax] таким образом, что gmin = 1/gmax. Когда σ <0, тогда F представляет большее уменьшение выгоды, чем увеличение (gmin <1/gmax). И, наоборот, λ > 0 представляет собой большее увеличение усиления, чем уменьшение. Например, рассмотрим диски, параметризованные α = 0.5 и тремя различными перекосами, λ = -2, 0 и 2.

diskmarginplot(0.5,[-2 0 2],'disk')

Figure contains an axes. The axes with title Values of multiplicative factor F contains 4 objects of type patch, line. These objects represent alpha = 0.5, skew = -2, alpha = 0.5, skew = 0, alpha = 0.5, skew = 2.

Каждая пара α, λ соответствует диску, который моделирует различный диапазон изменения усиления DGM = [gmin, gmax]. Проверьте изменения коэффициента усиления, соответствующие каждому из этих трех дисков.

Ranges = dm2gm(0.5,[-2  0 2])

Ranges = 3×2

    0.3333    1.4000
    0.6000    1.6667
    0.7143    3.0000

diskmarginplot(Ranges)

Figure contains an axes. The axes with title Range of gain and phase variations contains 3 objects of type patch. These objects represent DGM = [0.333,1.4], DPM = 32.2, DGM = [0.6,1.67], DPM = 28.1, DGM = [0.714,3], DPM = 32.2.

Сбалансированный λ = 0 диапазон симметричен вокруг номинального значения, позволяя коэффициенту усиления увеличиваться или уменьшаться примерно на 1,67. Отрицательное λ значение соответствует большему уменьшению усиления, чем увеличению, в то время как положительное λ дает большее увеличение, чем уменьшение.

umargin блок проектирования управления использует эту модель для представления коэффициента усиления и фазовой неопределенности в контуре обратной связи, устанавливая значения коэффициента усиления и запаса фазы, заданные при создании блока. diskmargin команда использует эту модель для вычисления коэффициента усиления на основе дисков и полей фаз, как описано в следующем разделе.

Поля диска для циклов SISO

Открыть сценарий в реальном времени

Для петлевого переноса L и заданного перекоса, diskmargin команда находит наибольший размер диска α, при котором система с замкнутым контуром feedback(L*F,1) стабилен для всех значений F. Это значение α называется запасом диска. Запас усиления на основе дисков DGM и запас фазы на основе дисков DPM представляют собой диапазон изменений усиления и фазы, представленный соответствующим диском.

Например, вычислить запас диска и связанный с ним коэффициент усиления на основе диска и поля фазы для передаточной функции SISO, используя значение по умолчанию, δ = 0.

sigma = 0;
L = tf(25,[1 10 10 10]);
DM = diskmargin(L,sigma);  
alpha = DM.DiskMargin

alpha = 0.4581

DGM = DM.GainMargin

DGM = 1×2

    0.6273    1.5942

DPM = DM.PhaseMargin

DPM = 1×2

  -25.8017   25.8017

Для этой системы сбалансированный (λ = 0) запас диска α составляет около 0,46. Соответствующий запас усиления на основе диска DGM показывает, что система остается стабильной для относительных вариаций усиления между примерно 0,63 и 1,6, или для фазовых вариаций около ± 26 градусов. Этот результат устанавливает стабильность для всех значений F на диске :

diskmarginplot(DGM,'disk')

Figure contains an axes. The axes with title Values of multiplicative factor F contains 8 objects of type patch, line, text.

Поля усиления представляют собой пересечение диска с действительной осью. Фазовый запас - это наибольший угол между действительной осью и линией, проходящей через исходную касательную к диску.

Комбинированные изменения коэффициента усиления и фазы

Маржа прибыли DGM вы получаете от diskmargin предполагать отсутствие фазовых вариаций и полей фаз DPM предполагать отсутствие изменения коэффициента усиления. На практике система может испытывать одновременные изменения коэффициента усиления и фазы. diskmarginplot позволяет визуализировать диапазоны одновременного усиления и фазовых изменений, допускаемых системой.

diskmarginplot(DGM)

Figure contains an axes. The axes with title Range of gain and phase variations contains 5 objects of type patch, text, line.

Затененная область показывает стабильный диапазон комбинированных изменений усиления и фазы. Таким образом, например, без изменения фазы система может выдерживать полный диапазон. DGM изменения коэффициента усиления, приблизительно от -4 дБ до 4 дБ. Если допускается изменение фазы на ± 17 градусов или около того, допустимое изменение коэффициента усиления падает до диапазона от -3 дБ до 3 дБ.

Поля диска и перекос

Диапазоны, показанные выше, вычисленные для λ = 0, представляют сбалансированную вариацию усиления, где gmin = 1/gmax. Изменение перекоса может показать, является ли контур более чувствительным к увеличению или уменьшению усиления. Например, при использовании λ > 0 может быть обнаружено, что контур обратной связи очень надежен для увеличения усиления, потому что положительные λ модели больше увеличивают усиление, чем уменьшают. Этот результат, однако, мало говорит о надежности, чтобы получить снижение. Попробуйте вычислить коэффициент усиления на основе дисков и фазовые поля для L, смещая его в сторону увеличения или уменьшения коэффициента усиления.

DMdec = diskmargin(L,-2);
DMinc = diskmargin(L,2); 
DGMdec = DMdec.GainMargin

DGMdec = 1×2

    0.4013    1.3745

DGMinc = DMinc.GainMargin

DGMinc = 1×2

    0.7717    1.7247

В совокупности эти результаты показывают, что при отсутствии фазовых изменений стабильность поддерживается для относительных изменений усиления между 0,4 и 1,72. Чтобы увидеть, как фазовый запас зависит от этих изменений усиления, постройте график стабильных диапазонов усиления и фазовых изменений для каждого diskmargin результат.

diskmarginplot([DGMdec;DGM;DGMinc])
legend('\sigma = -2','\sigma = 0','\sigma = 2')
title('Stable range of gain and phase variations')

$Figure contains an axes. The axes with title Stable range of gain and phase variations contains 3 objects of type patch. These objects represent \sigma = -2, \sigma = 0, \sigma = 2.$

Этот график показывает, что контур обратной связи может допускать большие изменения фазы, когда коэффициент усиления уменьшается. Другими словами, стабильность петли более чувствительна к увеличению усиления. Обратите внимание, что было бы неверно просто взять наибольший заявленный запас фазы (почти 30 градусов для λ = -2). Действительно, это большое значение основано на небольшом увеличении коэффициента усиления менее 3 дБ. Поскольку как усиление, так и фаза в целом подвержены неопределенности, важно обратить внимание на комбинированные вариации. Например, график показывает, что при увеличении коэффициента усиления на 4 дБ запас по фазе падает менее чем до 15 градусов. В противоположность этому, он остается больше 30 градусов, когда коэффициент усиления уменьшается на 4 дБ.

В заключение следует отметить, что изменение величины перекоса (λ) может дать более полную картину чувствительности к коэффициенту усиления и фазовой неопределенности. Если вы в основном не обеспокоены вариациями усиления в одном направлении (увеличение или уменьшение), не рекомендуется делать выводы из одного ненулевого значения λ. Вместо этого для получения несмещенных оценок коэффициента усиления и полей фазы используйте значение по умолчанию, δ = 0. При использовании ненулевых значений λ используйте как положительные, так и отрицательные значения для сравнения относительной чувствительности к увеличению усиления по сравнению с уменьшением усиления.

Диск неопределенности в плоскости Найквиста

Требование надежной устойчивости системы с замкнутым контуром feedback(L*F,1) эквивалентно требованию, 1 + L*F ≠ 0. В плоскости Найквиста это требование становится L (jλ) ≠ -1/F. Таким образом, диск F для каждого значения λ определяет область исключения, в которую кривая Найквиста не входит, если сохраняется стабильность по замкнутому контуру. Все такие диски -1/F содержать критическую точку (-1,0) и являются касательными к кривой Найквиста. Наклон регулирует размер и положение касательных дисков, как показано на следующем графике, на котором показаны области исключения для трех полей диска L, вычисленных выше. По мере увеличения, каждый диск обеспечивает более низкие оценки классического усиления и полей фазы.

nyquist(L)
hold on
diskmarginplot([DGMdec;DGM;DGMinc],'nyquist')
p = findobj(gca,'type','patch');
legend(p,'\sigma = -2','\sigma = 0','\sigma = 2')
hold off

$Figure contains an axes. The axes contains 9 objects of type line, patch. These objects represent L, \sigma = 2, \sigma = 0, \sigma = -2.$

Дополнительные сведения о интерпретации Nyquist диска неопределенности см. в разделах Запас диска и наименьшее дестабилизирующее возмущение.

Модель неопределенности MIMO и поля диска контуров обратной связи MIMO

Для систем MIMO модель применяет независимый диск _Fj неопределенности к каждому каналу цикла, заданный

$_{Fj} \frac{= 1 + α [(1 -_{}}{_{}}$

Модель заменяет ответ L с разомкнутым контуром MIMO на L * F, где

$F = \begin{matrix} _{(} \\ _{} \end{matrix} F1000⋱000FN$ ).

Аналогично случаю SISO, запас диска является наибольшим значением α, для которого система с замкнутым контуром feedback(L*F,eye(N)) является стабильным для всех значений F. Может быть полезно учитывать независимые вариации по всем каналам обратной связи одновременно, а также вариации по отдельным каналам. Поэтому diskmargin позволяет вычислять:

Поля петли в момент времени - максимально допустимые вариации усиления (или фазовые вариации) в каждом канале обратной связи, вычисленные со всеми остальными замкнутыми контурами. Анализ по контуру времени эффективно устанавливает все _δj в 0 для всех каналов, за исключением анализируемого канала.
Многолучевые поля - максимально допустимые вариации усиления (или фазовые вариации) по всем каналам обратной связи. Многолучевые поля допускают независимые вариации во всех каналах обратной связи одновременно. Способность улавливать такие петлевые взаимодействия является ключевым преимуществом подхода «диск-маржа» по сравнению с классическим анализом маржи. Многолучевый анализ обычно дает меньшие поля, чем анализ цикла за один раз.

Например, рассмотрим 2-канальную систему MIMO из следующей иллюстрации.

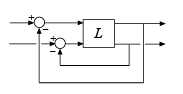
Для этой системы можно вычислить:

Максимально допустимые изменения коэффициента усиления (или изменения фазы) в первом канале (первый системный вход на первый системный выход)
Максимально допустимые изменения коэффициента усиления (или изменения фазы) во втором канале (второй системный вход на второй системный выход)
Максимально допустимые независимые вариации усиления (или фазовые вариации) в обоих каналах одновременно.

Для получения подробной информации и примеров получения этих полей цикла и многолучевого цикла см. diskmargin.

Отклонения на входе завода или выходе завода

В некоторых случаях пределы устойчивости могут изменяться в зависимости от того, применяются ли изменения коэффициента усиления и фазы на входе установки или на выходе установки. diskmargin позволяет вычислять поля для вариаций на входе, выходе или обоих одновременно. В целом, поля для одновременных изменений на входе и выходе меньше, чем поля только на входе или выходе, и обеспечивают более консервативную гарантию стабильности. Рассмотрим систему с замкнутым контуром SISO или MIMO следующей схемы.

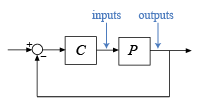
Поля на дисках на заводских входах и выходах можно вычислить следующим образом.

[DM,MM] = diskmargin(P*C) возвращает поля для вариаций на выходе завода.
[DM,MM] = diskmargin(C*P) возвращает поля для вариаций на заводских входах.
MMIO = diskmargin(P,C) возвращает запас для одновременных вариаций на выходах и входах установки. При сравнении этого запаса с полями на входах или выходах используйте 2*MMIO.Diskmargin, для учета одновременных возмущений, применяемых как на входах, так и на выходах.

Частотная зависимость полей

Как правило, коэффициенты усиления и поля фазы варьируются в зависимости от частоты. Это изменение обусловлено изменением частоты отклика с разомкнутым контуром L: Для каждой частоты λ существует различная наибольшая α (λ) такая, что I + L (jλ) F является обратимой для всех значений F в диске. Это значение является первым α (λ), для которого полюс с замкнутым контуром пересекает ось jλ на частоте, становясь нестабильным.

Поскольку запас α диска изменяется по частоте, то же самое происходит и с соответствующим допустимым диапазоном усиления или фазовых изменений. Построение этих дисковых полей как функции частоты обеспечивает информацию о полосах частот со слабыми полями.

L = tf(25,[1 10 10 10]);
diskmarginplot(L)

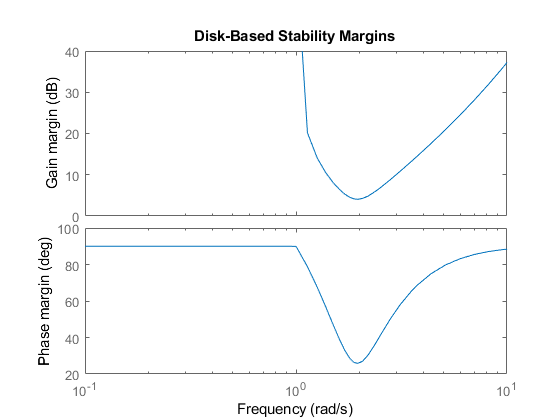
Disk margin plot showing disk-based gain and phase margins as a function of frequency

Поля диска, возвращенные diskmargin являются минимальными такими значениями для всех частот. Щелкните правой кнопкой мыши график, созданный diskmarginplot для подсказки данных с информацией об этих значениях.

Наихудшие поля диска

Запас диска вычисляется путем применения неопределенности к номинальной передаче L цикла и вычисления того, насколько большой может быть эта неопределенность при сохранении стабильности замкнутого цикла. Если передача цикла L сама по себе является неопределенной системой, то запас диска также изменяется в зависимости от других неопределенностей в системе. Наихудший запас диска - это наименьший запас диска, который возникает в пределах диапазонов неопределенностей, смоделированных в L. Он также является минимальным гарантированным запасом в диапазоне неопределенностей.

Вычисление наихудших дисковых полей неопределенной системы с помощью wcdiskmargin. Эта функция оценивает поля диска в наихудшем случае и соответствующие поля усиления и фазы в наихудшем случае как для вариаций цикла в момент времени, так и для многолучевых вариаций. Функция также возвращает наихудшее возмущение, комбинацию неопределенных элементов в L, которая дает самые слабые поля. Вы можете визуализировать наихудшие дисковые поля с помощью wcdiskmarginplot.

Поля диска и настройка системы управления

Настройка с помощью `systune` или настройка системы управления

Инструменты настройки системы управления в Toolbox™ Система управления позволяют указать целевое усиление и поля фаз для петель в настроенной системе. Цели настройки TuningGoal.Margins (для настройки командной строки с помощью systune) и Margins Goal (для настройки с помощью настройки системы управления) используют дисковые поля. Таким образом, когда вы указываете независимый коэффициент усиления и поля фазы GM и PM для настройки, программное обеспечение выбирает наименьший α, который обеспечивает оба значения. Это α задаётся:

$α = \frac{\max [}{GM -} 1GM + 1, тан$ (PM/2)].

Применяя это значение α, программное обеспечение настройки предполагает λ = 0.

Визуализация целей маржи с помощью viewGoal или графики цели настройки тюнера системы управления эквивалентны diskmarginplot(L), где L - настроенный отклик с разомкнутым контуром.

Надежный дизайн с помощью `musyn`

При выполнении надежной настройки контроллера с помощью musyn, вы можете моделировать усиление и фазовые вариации непосредственно в вашей системе с помощью umargin. Затем, выполнение надежной конструкции контроллера с musyn обеспечивает надежную стабильность для моделируемого диапазона усиления и фазовых изменений. Этот подход полезен, поскольку позволяет изучить влияние ожидаемого усиления и фазовых изменений на все аспекты производительности системы, используя ту же модель, что используется для настройки. Пример см. в разделе Надежный контроллер для вращающегося спутника.

Недостатком этого подхода является то, что musyn не только обеспечивает надежную стабильность во всем моделируемом диапазоне неопределенности. Она также пытается обеспечить надежную производительность. (См. раздел Измерение надежной производительности для синтеза Mu.) Достижение этого более строгого требования обычно невозможно или приводит к недопустимому ухудшению номинальной производительности. Таким образом, может потребоваться уменьшить моделируемый коэффициент усиления и фазовые изменения для поддержания разумной производительности. systune и Control System Tuner не имеют этого недостатка, потому что они обрабатывают маржинальные цели независимо от каких-либо целей производительности.

Ссылки

[1] Блайт, Джеймс Д., Р. Лейн Дейли и Дагфинн Гангсаас. «Практическое проектирование закона контроля для летательных аппаратов с использованием многовариантных методов». Международный журнал контроля 59, № 1 (январь 1994 года): 93-137. https://doi.org/10.1080/00207179408923071.

[2] Зайлер, Питер, Эндрю Паккард и Паскаль Гахинет. «Введение в поля диска [примечания к лекциям]». Журнал систем управления IEEE 40, № 5 (октябрь 2020): 78-95.

См. также

diskmargin | diskmarginplot | umargin | wcdiskmargin

Документация