Exponenta Banner
exponenta event banner

ncfmargin

Рассчитать нормированный запас остойчивости коферм контура обратной связи установки-контроллера

свернуть все на странице

Синтаксис

[marg, freq] = ncfmargin (P, C)
[marg, freq] = ncfmargin (P, C, знак)
[marg, freq] = ncfmargin (___, tol)

Описание

пример

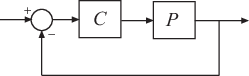
[marg,freq] = ncfmargin(P,C) возвращает нормализованный предел остойчивости многомерного контура обратной связи, состоящего из контроллера C в отрицательной обратной связи с заводом P:

Нормализованный второй предел устойчивости (также называемый пределом устойчивости метрики зазора) является показателем устойчивости к неструктурированным возмущениям. Значения, превышающие 0,3, обычно указывают на хороший запас прочности.

[marg,freq] = ncfmargin(P,C,sign) указывает знак соединения обратной связи, принимаемый для расчета запаса. По умолчанию sign = -1. Набор sign = +1 для соединения с положительной обратной связью.

[marg,freq] = ncfmargin(___,tol) вычисляет нормированный коэффициент коприма с заданной относительной точностью.

Примеры

свернуть все

Открыть сценарий в реальном времени

Рассмотрим нестабильный завод первого порядка, p, стабилизированный контроллерами с высоким и низким коэффициентом усиления, cL и cH.

p = tf(4,[1 -0.001]); 	
cL = 1;				
cH = 10;

Вычислите запас устойчивости системы с замкнутым контуром с помощью контроллера с низким коэффициентом усиления.

[margL,~] = ncfmargin(p,cL)
margL = 0.7069

Аналогично, вычислите запас устойчивости системы с замкнутым контуром с помощью контроллера с высоким коэффициентом усиления.

[margH,~] = ncfmargin(p,cH)
margH = 0.0995

Системы с замкнутым контуром с контроллерами с низким коэффициентом усиления и с высоким коэффициентом усиления имеют нормированные пределы устойчивости к параллелизму, равные примерно 0,71 и 0,1 соответственно. Этот результат указывает, что система с замкнутым контуром с контроллером с низким коэффициентом усиления более устойчива к неструктурированным возмущениям, чем система с контроллером с высоким коэффициентом усиления.

Чтобы наблюдать эту разницу в надежности, постройте неопределенное растение, punc, что имеет дополнительную немодулированную динамику на высокой частоте по сравнению с номинальной установкой.

punc = p + ultidyn('uncstruc',[1 1],'Bound',1);
sigma(p,punc,'r--')

Figure contains an axes. The axes contains 22 objects of type line. These objects represent p, punc.

Рассчитайте устойчивую стабильность систем с замкнутым контуром, сформированных неопределенной установкой и каждым контроллером.

[stabmargL,~] = robstab(feedback(punc,cL))
stabmargL = struct with fields:
           LowerBound: 0.9980
           UpperBound: 1
    CriticalFrequency: Inf


[stabmargH,~] = robstab(feedback(punc,cH))
stabmargH = struct with fields:
           LowerBound: 0.0998
           UpperBound: 0.1000
    CriticalFrequency: Inf

Как и ожидалось, надежный анализ стабильности показывает, что система с замкнутым контуром с контроллером с низким коэффициентом усиления более устойчива в присутствии немодулированной динамики LTI. Фактически, эта замкнутая система может выдерживать почти 100% указанной неопределенности. В отличие от этого система с замкнутым контуром с контроллером с высоким коэффициентом усиления может выдерживать только около 10% заданной неопределенности.

Открыть сценарий в реальном времени

Рассмотрим установку и стабилизирующий контроллер. 

P1 = tf([1 2],[1 5 10]);
C = tf(4.4,[1 0]);

Вычислите запас устойчивости для этого завода и контроллера. 

b1 = ncfmargin(P1,C)
b1 = 0.1961

Затем вычислите промежуток между P1 и возмущенное растение, P2.

P2 = tf([1 1],[1 3 10]);
[gap,nugap] = gapmetric(P1,P2)
gap = 0.1391

nugap = 0.1390

Потому что запас устойчивости b1 = b(P1,C) больше, чем зазор между двумя растениями, C также стабилизирует P2. Как обсуждалось в Gap Metrics and Stability Margins, запас устойчивости b2 = b(P2,C) удовлетворяет неравенство asin(b(P2,C)) ≥ asin(b1)-asin(gap). Подтвердите этот результат. 

b2 = ncfmargin(P2,C);
[asin(b2) asin(b1)-asin(gap)]
ans = 1×2

    0.0997    0.0579

Входные аргументы

свернуть все

Установка, заданная как динамическая модель системы. P может быть SISO или MIMO, если P*C имеет одинаковое количество входов и выходов. P может быть непрерывным временем или дискретным временем. Если P является обобщенной государственно-пространственной моделью (genss или uss) затем ncfmargin использует текущее или номинальное значение всех блоков проекта управления в P.

Установка, заданная как динамическая модель системы. C может быть SISO или MIMO, если P*C имеет одинаковое количество входов и выходов. C может быть непрерывным временем или дискретным временем. Если C является обобщенной государственно-пространственной моделью (genss или uss) затем ncfmargin использует текущее или номинальное значение всех блоков проекта управления в P.

По умолчанию ncfmargin предполагает взаимосвязь отрицательной обратной связи между P и C. Чтобы вычислить поля для замкнутой системы с положительной обратной связью, используйте [marg,freq] = ncfmargin(P,C,+1).

Знак соединения обратной связи, указанный как -1 или +1.

Значение по умолчанию, sign = -1, указывает отрицательную обратную связь. Настройка sign = +1 предполагает положительную обратную связь для расчета маржи, как показано на следующей диаграмме.

Относительная точность для вычисленного запаса, заданного как положительное скалярное значение меньше 1. Значение по умолчанию - 0,001, или 0,1% точности.

Выходные аргументы

свернуть все

Нормализованный совместимый запас устойчивости, возвращаемый как скаляр в диапазоне [0,1]. Эта величина, также известная как запас устойчивости метрики зазора, является показателем устойчивости по замкнутому контуру к неструктурированным возмущениям. Для архитектуры управления с отрицательной обратной связью она определяется как:

b (P, C) = ‖ [IC] (I + PC) − 1 [IP] ‖ ∞−1= ‖ [IP] (I + CP) − 1 [IC] ‖ ∞−1.

Значения, превышающие 0,3, обычно указывают на хороший запас прочности. Если система с замкнутым контуром нестабильна, то marg = 0. Величина b (P, C) -1 представляет собой усиление сигнала от возмущений на входе и выходе установки на вход и выход контроллера.

Частота, при которой запас marg возникает, возвращается как скаляр. Если система с замкнутым контуром нестабильна, то freq = NaN.

Подробнее

свернуть все

Показатели запаса устойчивости и разрыва

Запас устойчивости b (P, C) связан с метрикой зазора, которая дает числовое значение δ (P1,P2) для расстояния между двумя системами LTI ( см.gapmetric).

Для метрик как gap, так и start-gap сохраняется следующий надежный результат производительности:

arcsin b (P2,C2) ≥ arcsin b (P1,C1) - arcsin δ (P1,P2) - arcsin δ (C1, С2),

Чтобы интерпретировать этот результат, предположим, что номинальная P1 установки стабилизируется контроллером C1 с запасом устойчивости b (P1, C1). Затем, если P1 возмущается до P2 и C1 возмущается до C2, предел устойчивости ухудшается не более чем на указанную выше формулу.

λ-зазор всегда меньше или равен зазору, поэтому его прогнозы с использованием вышеуказанного результата надежности более жесткие.

Совет

  • В то время как ncfmargin предполагает цикл отрицательной обратной связи, ncfsyn команда создает контроллер для цикла положительной обратной связи. Поэтому вычислять запас с помощью контроллера, разработанного с помощью ncfsyn, использовать [marg,freq] = ncfmargin(P,C,+1).

Алгоритмы

Расчет нормированного запаса устойчивости коприма описан в главе 16 из [1].

Ссылки

[1] Чжоу, К., Дойл, J.C., Основы надежного контроля. Лондон, Великобритания: Пирсон, 1997.

См. также

| | | |

Представлен до R2006a

Документация по инструментам надежного управления

Поддержка